Mouvement d'un projectile : concours orthoptie Rennes 2011.

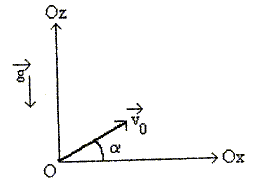L'espace est repéré par un repère cartésien d'origine O d'axes (Ox, Oy, Oz , lié à la surface de la terre. L'axe Oz est vertical ascendant, le plan (Ox, Oy) est horizontal. Un opérateur projette un solide S ponctuel de masse m =120 g du point O à t=0 avec une vitesse v0 contenue dans le plan (Ox, Oz ) et faisant un angle alpha = 30 ° acec l'axe Ox. On suppose que le solide n'est soumis à aucune action de l'air. Le référentiel terrestre est supposé galiléen ; g = 9,8 m s-2 ; v0 = 11 m /s. Rappeler les trois lois de Newton pour un système matériel. 1ère loi de Newton Un référentiel galiléen est un référentiel dans lequel le principe de l’inertie est vérifié. Dans un référentiel galiléen, si la somme vectorielle des forces extérieures appliquées à un solide est nulle ( solide pseudo-isolé ) alors le centre d’inertie G de ce solide est soit au repos, soit animé d'un mouvement rectiligne uniforme et réciproquement. 2ème loi de Newton Dans un référentiel galiléen, si le vecteur vitesse du centre d'inertie d'un solide varie, alors la somme vectorielle des forces extérieures appliquées à ce solide n'est pas nulle et réciproquement. La direction et le sens de cette somme sont ceux de la variation du vecteur vitesse entre deux instants proches. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie. 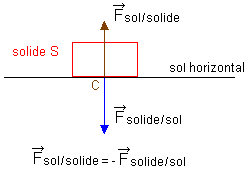3ème loi de Newton Interaction entre un objet A et un objet B : si un solide noté A exerce sur un solide noté B une force notée F A / B, alors B exerce sur A une force notée F B / A . Les deux forces associées à une même interaction sont toujours égales et opposées. Le solide est-il en chute libre ? Déterminer les équations littérales horaires du mouvement du solide pour t >0. Le solide n'est soumis qu'à son poids : la chute est dite "libre". accélération : ( 0 ; -g) vitesse initiale (v0cos a ; v0 sin a ) position initiale : origine du repère. vitesse, primitive de l'accélération : v0cos a ; -gt +v0 sin a . position, primitive de la vitesse : x= v0cos a t  ; z = -½gt² + v0 sin a t. En déduire l'équation littérale de la trajectoire. Caractériser le mouvement. trajectoire ( éliminer le temps dans les deux relations précédentes): t= x/( v0cos a) puis repport dans z z= -½gx²/(v0cosa)² + x tan a. Mouvement uniformément accéléré ; trajectoire parabolique. Au sommet S de la trajectoire, que vaut la composante verticale de la vitesse ? En déduire la durée nécessaire pour atteindre le sommet. En S, la composante verticale de la vitesse est nulle. -gt +v0 sin a=0 ; t = v0 sin a/g = 11 sin 30  / 9,8 =0,5612 ~0,56 s.   Quelles sont les coordonnées du point S ? repport dans z(t) : zS= -½g v²0 sin² a/g² + v²0 sin² a/g = ½v²0 sin² a/g . zS = 0,5*112 sin230 /9,8 =1,543 ~1,5 m. xS= v0cos a v0 sin a/g= v²0 sin a cos a/g . xS =112 sin30 cos 30 /9,8 =5,346 ~5,3 m. On cherche à connaître à quelle distance xmax, le projectile touche le sol. Le sol est horizontal et situé à 1,3 m en dessous du point O. Quelle est la valeur de z lorsque le projectile touche le sol ?      z = -1,3 m.        En déduire la durée du vol du projectile. z = -½gt² + v0 sin a t ; -1,3 = -4,9 t2 +11*sin 30 t ; t2 -1,1224 t-0,2653 ; D = 1,260 +1,061 = 2,32 ; D½ =1,52. t =( 1,1224+1,52) / 2 =1,33 ~1,3 s. En déduire xmax.     xmax= v0cos a t  = 11 *cos 30 *1,33 =12,67  ~13 m.                                                                                                                                       On prend z = 0 comme origine de l'énergie potentielle de pesanteur. Déterminer la valeur de l'énergie mécanique du solide au moment du lancer. Le solide est en O, origine de l'énergie potentielle ; l'énergie mécanique est sous forme cinétique ½mv02 =0,5 *0,120*112 =7,26 ~7,3 J. Déterminer l'énergie mécanique  du système en S et en xmax. Seul le poids travaille, l'énergie mécanique du solide reste constante, égale à 7,3 J.

menu