Détermination des caractéristiques d'une bobine : concours orthoptie Rennes 2011.

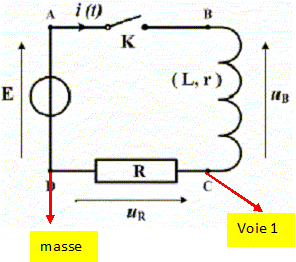
Etude du régime transitoire d'un circuit RL. On réalise un circuit composé en série d'un générateur de tension continue ( E =5,0 V ), d'un interrupteur K, d'une résistance ( R = 5,0 ohms ) et de la boine étudiée ( L et r  inconnus ). Faire le schéma du circuit. 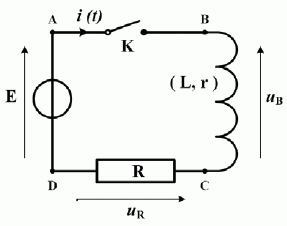Initialement l'interrupteur est ouvert. A la date t=0, on le ferme.  En expliquant précisément les notations adoptées, établir l'équation différentielle de l'intensité i du courant dans le circuit pour t >0. Additivité des tensions : E = uR + uB ; de plus uR = Ri ; uB = Ldi/dt + ri. E =(R+r)i + Ldi/dt. (1) Donner la solution de l'équation différentielle. Solution générale de (R+r)i + Ldi/dt =0. On pose t = L/(R+r). i(t) = A exp (-t/ t). Solution particulière de (1) en régime permanent  : I =E / (R+r) Solution générale de (1) : i(t) = A exp (-t/ t) + E / (R+r). A t = 0, la continuité de l'énergie stockée dans labobine impose i(t=0) =0, d'où :0 = A +E / (R+r) ; A = -E / (R+r). i(t) = E / (R+r) ( 1-exp (-t/ t)  ). 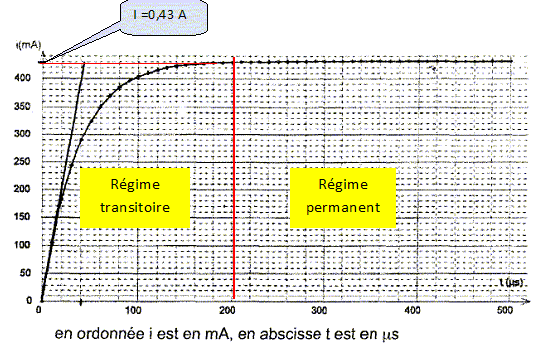On souhaite à l'aide d'un ordinateur muni d'une interface d'acquisition, déterminer expérimentalement l'évolution de i, lors de la fermeture de l'interrupteur. Indiquer les branchements à réaliser. Quel traitement doit-on faire à l'ordinateur pour avoir i(t) ? La tension aux bornes du conducteur ohmique R et l'intensité qui le traverse sont proportionnelles. On visualise la tension uR ; pour avoir i(t) on divise uR par R. La courbe représentant i(t) est la suivante : Nommer les deux régimes observés ; quelle est la valeur de l'intensité en régime permanent ? 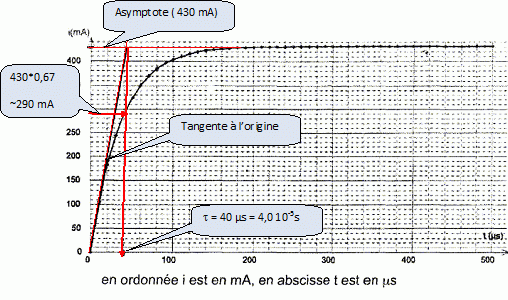En déduire la valeur de r. I = E /(R+r) ; r = E/I -R = 5,0/0,43-5 =6,63 ~6,6 ohms. A partir de la courbe, déterminer la constante de temps t et en déduire la valeur de L. L = t(R+r) =4,0 10-5 *(5,0+6,63) =4,65 10-4 ~0,47 mH. 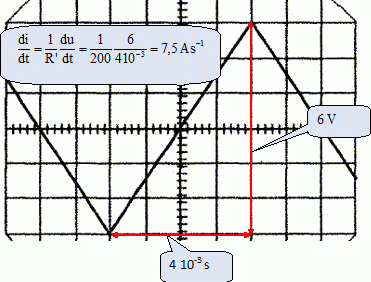Réponse à une tension triangulaire. Le générateur de tension continue est remplacé par un GBF qui délivre une tension triangulaire. La résistance R est remplacée par R' = 200 ohms. On négligera la résistance r' de la bobine devant R'. A l'aide d'un oscilloscope on visualise la tension aux bornes de la résistance R' ( sensibilite horizontale 1,0 ms / div ; sensibilité verticale 1,0 V / div. 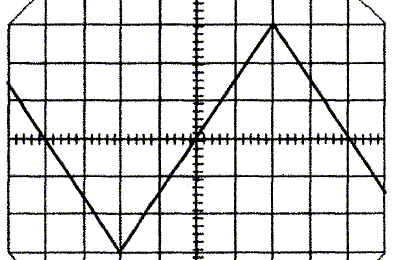  En déduire la valeur di/dt lorsque la courbe est croissante. Quelle relation lie di/dt à la tension uL aux bornes de la bobine ? uL = L di/dt. On visualise simultanément uL et uR'. uL est une tension crénaux de + ou - 3,0 mV. En déduire la valeur de L. L = uL / (di/dt) = 3 10-3 / 7,5 =4,0 10-4 H = 0,40 mH. Etude de la décharge oscillante dans un circuit RLC. On souhaite observer les oscillations électriques libres en insérant la bobine dans un circuit RLC série. Proposer le schéma d'un montage permettant de raliser de telles oscillations. Faire figurer sur le schéma les branchements de la carte d'acquisition d'un ordinateur. Le condensateur étant initialement chargé, à la date t = 0, on bascule l'interrupteur de la position (1) vers la position (2). Le système d'acquisition relié à l'ordinateur permet d'enregistrer la courbe d'évolution de la tension u aux bornes du condensateur en fonction du temps. C est relié à la masse et A à la voie 1 de l'interface. Quels sont les différents régimes possibles ?       Courbe 5 : périodique ; courbe 6 : pseudopériodique ; courbe 4 : apériodique.                                                                                                                                                        On mesure une pseudo-période T = 8,6 ms avec C = 4,7 mF. En déduire la valeur de L. T = 8,6 10-3 s ; C = 4,7 10-3 F. T = 2p(LC)½ ; L = T2/(4p2C) =(8,6 10-3)2/(4*3,142*4,7 10-3 )= 3,99 10-4 ~4,0 10-4 H.

menu