QCM physique (tobogan de plage, acoustique : écoute sur la plage ) : concours médecine

Aurélie 08/09/11

   QCM physique (tobogan de plage, acoustique : écoute sur la plage ) : concours médecine.

Tobogan de plage.
Dans un parc d’attraction, on installe le toboggan d’eau ci-contre. La hauteur du point d’injection d’eau, en A, vaut H = 10 m, celle du point de sortie du toboggan, vaut L = 2 m. Le niveau d’eau dans la piscine (en B)
est situé à une hauteur h = 1 m plus bas que le point de sortie du toboggan. Le niveau d’eau en B est stable. La taille de la pompe et les épaisseurs des canalisations et de la coulée d’eau sur le toboggan sont
négligeables devant les hauteurs du système (contrairement au dessin). Le circuit d’eau est continu, permanent et alimenté par une pompe électrique située entre les points D et E pour compenser les pertes par frottements dans les tuyaux CD et EA. Les frottements sont négligeables dans le reste du circuit. La canalisation CD a une section S = 0.01 m², un rayon r_CD et une longueur l_CD. La canalisation EA a un rayon r_EA = r_CD/2 et une longeur l_EA = l_CD/2. Les pertes de Poiseuille dans le tronçon CD sont estimées à |Δp_CD| = 6000 Pa. On mesure une vitesse v_A = 0.5 m/s de l’eau en A. On note p_atm la pression atmosphérique, g ≈ 10 m s^-2 l’accélération de la
pesanteur et ρ = 10³ kg m^-3 la masse volumique de l’eau.
Un pingouin, de masse m = 20 kg, s’élance en A à la même vitesse v_A que l’eau. Il glisse sans frotter, puis plonge dans la piscine.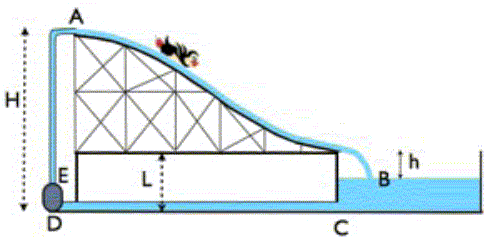

Cocher la ou les propositions vraies concernant la pression de l’eau le long du toboggan :
A. Elle diminue en descendant ; B. Elle est uniforme le long du toboggan ; C. Elle augmente en descendant
D. Elle est nulle ; E. Elle est égale à la pression atmosphérique en A.
L'eau est constamment en contact avec l'atmosphère et son épaisseur est faible. La pression de l'eau est égale à la pression atmosphérique tout le long du tobogan.

2.Cocher la ou les propositions vraies :
A. Le pingouin reçoit de l’énergie de l’attraction terrestre.
B. L’énergie potentielle du pingouin décroît pendant la descente.
C. L’énergie potentielle du pingouin augmente pendant la descente.
D. Le pingouin descend plus vite que l’eau.
E. Le pingouin descend moins vite que l’eau..
Le pingoin glisse sans frottement : il descend à la même vitesse que l'eau.
On choisit l'origine de l'énergie potentielle de pesanteur au point le plus bas, en B. L'énergie potentielle du pingoin diminue lors de la descente ; donc B.

On considère la variation ΔE de son énergie potentielle entre le point final B et le point initial A (final moins initial). Cocher la ou les propositions vraies :
A. ΔE a pour unité kg m² s^-2 ;
B. ΔE a pour unité kg m s^-1 ;
C. La variation d’énergie potentielle est opposée au travail de la résultante des forces agissant sur
le pingouin.
D. La somme de l’énergie cinétique du pingouin et du travail des forces qui agissent sur lui se
conserve.
E. La réaction du toboggan sur le pingouin travaille.
ΔE s'exprime en joule ; une nénergie est une force fois une distance et une force est une masse fois une accélération ; une accélération est une distance divisée par un temps au carré.
Joule = kg m² s^-2, donc A.
Le pingoin est soumis à son poids et à l'action du support, perpendiculaire au plan en absence de frottement ;
l'action du plan, perpendiculaire àla vitesse ne travaille pas. La variation d'énergie potentielle est l'opposée du travail du poids, , donc C.
La somme de l'énergie potentielle et de l'énergie cinétique est constante si seul le poids travaille.

4. Calculer ΔE. Cocher la ou les propositions vraies :
A. ΔE < 0 ; B. ΔE > 0 ; C. |ΔE| = 1600 J ; D. |ΔE| = 1800 J ; E. |ΔE| = 2000 J
L'altitude du centre d'inertie du pingoin diminue ; l'énergie potentielle diminue et DE<0, donc A.
DE = -mgh = -20*10*9 = -1800 J, donc D.

5. Calculer la vitesse v_IP d’impact du pingouin à la surface de la piscine. Cocher la ou les propositions vraies :
A. v_IP < v_A ; B. v_IP > v_A ; C. v_IP = (2gH)1/2 ; D. v_IP = 13.4 m/s ; E. v_IP = 14.1 m/s
Energie mécanique en A : mgH +½mv²_A ; énergie mécanique en B : mg(L-h) +½mv²_IP ;
Conservation de l'énergie mécanique : mgH +½mv²_A = mg(L-h) +½mv²_IP ;
2gH +v²_A = 2g(L-h) +v²_IP ; v²_IP = v²_A +2g(H-L+h) =v²_A +2g(H-L+h) , donc B.
v_IP =( 0,25 +20*9 )^½=13,4 m/s, donc D.

6. On étudie les vitesses de l’eau le long du circuit. Cocher la ou les propositions vraies :
A. la vitesse est constante le long du toboggan.
B. l’eau de la piscine, à la surface, a une vitesse v_B = v_IP.
C. la vitesse sur le tronçon CD vaut v_CD = v_A /4.
D. v_CD = v_A /2. E. v_CD = 4 v_A .
La vitesse de l'eau augmente lors de la descente ( chute d'eau ) ; la surface de la piscine est grande, la vitesse de l'eau en B est pratiquement nulle.
La canalisation CD a une section S = 0.01 m², un rayon r_CD. La canalisation EA a un rayon r_EA = r_CD/2 donc une section 4 fois plus petite que celle de la canalisation CD.
La conservation du débit volumique conduit à : v_EA =v_A = 4v_CD, donc C.

7. On étudie les pertes de Poiseuille Δp_CD et Δp_EA dans les tuyaux CD et EA, en valeur absolue. Cocher la ou les propositions vraies :
A. les pertes sont plus fortes dans le long tuyau CD.
B. Δp_CD / Δp_EA = 1/16 ; C. Δp_CD / Δp_EA = 1/8 ; D. Δp_CD / Δp_EA = 2 ; E. Δp_CD / Δp_EA = 32.

La loi de Poiseuille donne également les pertes de charge : D p = 8h L / (pr⁴) Q_v.
Le débit Q_v est le même ; longeur l_EA = l_{CD/2 ;}rayon r_EA = r_CD/2 ; Δp_CD = 8h l_CD / (pr_CD⁴) Q_v.
Δp_EA = 8h l_EA / (pr_EA⁴) Q_v = 8h ½l_CD / (p½r_CD⁴) Q_v = 8 x8 h l_CD / (pr_CD⁴) Q_v =8 Δp_CD. Δp_CD / Δp_EA =1/8, donc C.

8. On étudie l’écoulement visqueux de l’eau entre le point B à la surface de la piscine et le point D d’entrée de la pompe. On note p_B et p_D les pressions en ces points. Cocher la proposition vraie :
A. p_B + 0.5 ρ v_IP² + ρg (L-h) = p_D + 0.5 ρ v_CD² + Δp_CD ;
B. p_B + ρg (L-h) = p_D + 0.5 ρ v_CD² + Δp_CD
C. p_B + ρg (L-h) = p_D + 0.5 ρ v_CD² - Δp_CD
D. p_B + 0.5 ρ v_IP² + ρg (L-h) = p_D + 0.5 ρv_CD² - Δp_CD
E. aucune des équations précédentes n’est vraie
Bernoulli appliqué à un fluide réel avec pertes de charge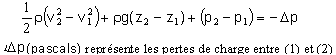
(1) correspond à B, (2) correspond à D
½ρ (v_CD² -v_B² ) + ρg (h-L) + p_D -p_B = - Δp_CDavec v_B~0 la surface de la piscine est grande, la vitesse de l'eau en B est pratiquement nulle.
p_B   + ρg (L-h) = p_D + ½ρ v_CD² + Δp_CD donc B.

9. On étudie l’écoulement visqueux de l’eau entre l’entrée de la pompe, D, et le haut du toboggan, A. On note Δπ la surpression, en valeur absolue, délivrée par la pompe. Cocher la ou les propositions vraies :
A. p_E = p_D + Δπ vrai.
B. p_E = p_D - Δπ
C. p_A + Δp_EA + 0.5 ρ v_A² + ρgH = p_D + Δπ + 0.5 ρv_CD²
D. p_A + Δπ + 0.5 ρ v_A² + ρgH = p_D + Δp_EA + 0.5 ρv_CD²
E. p_A + 0.5 ρ v_A² + ρgH = p_D + Δp_EA + Δπ + 0.5 ρv_CD²
Bernoulli appliqué à un fluide réel avec pertes de charge et avec une machine de puissance p ( débit volumique Q )
½ρ (v_A² -v_CD² ) + ρg H + p_A -p_D = - Δp_EA + Δπ ;
p_A + ½ρ v_A² + ρg H = p_D + ½ρ v_CD² - Δp_EA + Δπ ;donc C.

10. Calculer la surpression Δπ délivrée par la pompe. Cocher la proposition vraie :
A. Δπ = -1 atm ; B. Δπ = -0.5 atm ; C. Δπ = 0.4 atm ; D. Δπ = 1 atm ; E. Δπ = 1.4 atm.
Δπ =½ρ (v_A² -v_CD² ) + ρg H + p_A -p_D +Δp_EA ;
p_D = p_B   + ρg (L-h) - ½ρ v_CD² - Δp_CD ;
Δπ =½ρ (v_A² -v_CD² ) + ρg H + p_A -p_B - ρg (L-h) + ½ρ v_CD² + Δp_CD+Δp_EA ;
Δπ =½ρ v_A² + ρg (H+h-L) + p_A -p_B + Δp_CD+Δp_EAavec p_A =p_B = p_atm.
Δπ =500* 0,5² + 9 10⁴ + 6000+6000*8=144125 Pa ~ 1,4 atm, donc E.

11. On considère la puissance P mécanique que doit délivrer la pompe. Cocher la ou les propositions vraies :
A. P < 0 ; B. P > 0 ; C. |P| = S v_CD Δπ ; D. |P| = S vA Δπ ; E. la puissance P s’exprime en kg m² s^-3.
P >0 si le fluide reçoit de l'énergie de la machine (pompe) ; donc B.
Δπ = P / Q avec Q débit volumique Q = S v_CD; donc C.
Puissance (watt) =surface fois vitesse fois pression ; pression = force / surface ; force = masse fois accélération ;
P = vitesse *masse *accélération ( kg m² s^-3 ) ; donc E.

12.Cocher la proposition vraie :
A. |P| = 10 W ; B. |P| = 50 W ; C. |P| = 120 W ; D. |P| = 180 W ; E. |P| = 500 W.
|P| = S v_CD Δπ = 0,01*0,125 *144125 =180 W, donc D.

13. On considère la puissance P_el électrique qu’on doit fournir à la pompe qui a un rendement ε 90%. Cocher la ou les propositions vraies :
A. |Pel| = ε P ; B. |Pel| = P / ε vrai ; C. |Pel| = 130 W ; D. |Pel| = 200 W ; E. |Pel| = 450 W
180 /0,9 =200 W, donc D.

Acoustique : écoute sur la plage.
Fatigué(e) de la plongée et des descentes en toboggan, vous vous étendez sur la plage et vous écoutez le bruit des vagues et des conversations aux alentours. Le niveau d’intensité sonore de la mer à l’entrée du pavillon de l’oreille vaut L_mer= 40 dB. Chaque personne qui parle produit une onde sonore qu’on considérera comme sphérique avec un niveau sonore L₁(R) = 50 dB à une
distance R = 1 m d’elle. Vous comptez 10 personnes autour de vous, chacune à une distance moyenne D = 10 m.
Les ondes sonores atteignent le pavillon de votre oreille externe, de surface S_P = 6 cm². Grâce au conduit auditif, de longueur L = 2.5 cm, les ondes collectées par le pavillon sont guidées vers le tympan de surface S_T = S_P/8 en conservant la puissance sonore. On note Z_air l’impédance acoustique des milieux aériens traversés par l’onde sonore (conduit auditif externe et oreille moyenne située entre le tympan et la cochlée et comprenant les osselets). On note Z_tissusl’impédance acoustique moyenne des tissus traversés (membrane du tympan, membrane de la fenêtre ovale à l’entrée de la cochlée, et liquide de la cochlée). On rappelle que l’intensité de
référence des niveaux sonores vaut I_ref = 10^-12 W m^-2. La vitesse du son dans l’air vaut c = 340 m/s en ce beau jour d’été.
1. Calculer l’intensité I_mer et la puissance P_mer sonores qui pénètrent à l’entrée du pavillon de votre oreille, venant de la mer. Cocher la ou les propositions vraies :
A. I_mer = 10^-16 W m^-2 ; B. I_mer= 10^-8 W m^-2 ; C. I_mer = 4 10^-8 W m^-2 ; D. P_mer = 6.0 10^-12 W ; E. P_mer = 6.0 10^-8 W.
I_mer = I_ref * 10^{Lmer / 10} = 10^-12 * 10⁴ = 10^-8W m^-2, donc B.
P_mer = I_mer S_P =10^-8* 6 10^-4 =6.0 10^-12 W, donc D.

2. On note I₁(R) l’intensité sonore produite par la voix d’une personne à la distance R. Calculer la puissance sonore totale P₁ émise par cette voix dans toutes les directions. Cocher la proposition vraie :
A. P₁ = 4π R² I₁(R) ; B. P₁ = πR² I₁(R) ; C. P₁ = R I₁(R) ; D. P₁ = I₁(R) / (πR²) ; E. P₁ = I₁(R)/ (4π R²).
Puissance sonore (W) = intensité sonore (W m^-2) * aire (m²) de la sphère de rayon R, donc A.

3. Calculer l’intensité sonore I₁(D) qui atteint l’entrée du pavillon de votre oreille provenant de la voix d’une seule personne. Cocher la ou les propositions vraies :
A. I₁(D) = (R/D) I₁(R) ; B. I₁(D) = (R/D)² I₁(R) ; C. I₁(D) = P₁ / (4π D²) ;
D. I₁(D) = 10^-8 W m^-2 ; E. I₁(D) = 10^-9 W m^-2.
P₁ = I₁(R) 4π R² = I₁(D) 4π D² donc B, C.
I₁(R) = I_ref * 10^{L1(R) / 10} = 10^-12 * 10⁵ = 10^-7W m^-2 ; R/D = 0,1 ;
I₁(D) = (R/D)² I₁(R) =0,01 *10^-7 = 10^-9W m^-2, donc E.

4. On étudie l’intensité sonore I_P totale qui atteint le pavillon de votre oreille venant des bruits environnants, ainsi que le niveau sonore L_P correspondant. Cocher la ou les propositions vraies :
A. I_P = [I_mer² + 100 I₁(D)²]^1/2 ; B. I_P = I_mer + 10 I₁(D) ; C. L_P = 41.5 dB ; D. L_P = 43 dB ; E. L_P = 100 dB.
Les intensités sonores s'ajoutent, donc B.
I_P =10^-8 + 10 *10^-9 = 2 10^-8 W m^-2 ; L_P =10 log( 2 10^-8/ 10^-12) =43 dB, donc D.

5. Calculer la différence de niveau sonore, L_T-L_P entre le tympan et l’entrée du pavillon. Cocher la ou les propositions vraies :
A. L_T-L_P > 0 ; B. L_T-L_P < 0 ; C. L_T-L_P = 0 dB ; D. |L_T-L_P| = 9 dB ; E. |L_T-L_P| = 18 dB.
I_T = P / S_T ; I_P = P / S_P = P / (8S_T ) = I_T / 8 ;
L_T = 10 log ( I_T / I_réf) ; L_P = 10 log ( I_P / I_réf) =10 log ( I_T / (8I_réf) ) ; L_T > L_P, donc A.
L_T - L_P =10 log ( I_T / I_réf) - 10 log ( I_T / (8I_réf) ) = 10 log ( I_T / I_réf) - 10 log ( I_T / I_réf) + 10 log 8 = 9 dB, donc D.

6. On mesure un coefficient de transmission en intensité T = 10^-3 entre l’air et les tissus. Cocher la ou les propositions vraies :
A. T = |Z_air - Z_tissus| / (Z_air + Z_tissus) ; B. T = (Z_air - Z_tissus)²/ (Z_air + Z_tissus)² ;
C. T = 1 - (Z_air - Z_tissus)² / (Z_air + Z_tissus)² ; D. T = 4 Z_air Z_tissus / (Z_air + Z_tissus)² vrai ;
E. aucune des expressions ci dessus n’est vraie
1 - (Z_air - Z_tissus)² / (Z_air + Z_tissus)² =[ (Z_air + Z_tissus)² - (Z_air - Z_tissus)²] / (Z_air + Z_tissus)² = 4 Z_air Z_tissus / (Z_air + Z_tissus)², donc C.

7. On note I_T l’intensité de l’onde, de niveau sonore L_T, qui atteint le tympan au bout du conduit auditif, dans l’air. Calculer la perte relative d’intensité de l’onde sonore qui pénètre dans le liquide
de la cochlée par rapport à I_T. Cocher la ou les propositions vraies :
A. ΔI / I_T > 0 ; B. ΔI/I_T < 0 ; C. |ΔI/I_T| = 1 - T³ ; D. |ΔI/I_T| = 1 - 3T ; E. |ΔI/I_T| = (1 - T)³.
DI = (I_transmise- I_T ) ; DI / I_T= I_transmise / I_T -1 avec T =I_transmise / I_T ; DI / I_T= T-1, négatif, donc B.

8. Les osselets de l’oreille moyenne ont pour rôle d’éviter cette perte et d’amplifier mécaniquement la surpression sonore pour augmenter le niveau sonore L_c à l’entrée de la cochlée de 26 dB par
rapport à L_T. Calculer L_c pour l’ensemble des bruits environnants. Cocher la proposition vraie :
A. L_c = 26 dB ; B. L_c = 51 dB ; C. L_c = 60 dB ; D. L_c = 78 dB ; E. L_c = 85.5 dB.
L_P = 43 dB ; L_T - L_P = 9 dB ; L_T = 43+9 = 52 dB ; Lc = 26 +L_T = 78 dB, donc D.

9. Le vendeur de glaces marche vers vous à la vitesse v = 1 m/s, en sifflotant à la fréquence f = 500 Hz. Calculer la variation relative de fréquence (f ’-f)/f entre la fréquence f émise et celle f ’ que vous
percevez. Cocher la ou les propositions vraies :
A. le son perçu est plus aigu ; B. le son perçu est plus grave ; C. (f ’-f)/f = +0.29 % ; D. (f ’-f)/f = -0.29 % ; E. (f ’-f)/f = +2.9 %.
Effet Doppler : f ' =c/(c-v) f = 340/339 *500 = 501,47 Hz, la fréquence étant plus élevée, le son est plus aigu, donc A.
(f ' -f) / f =1,147 / 500 =2,9 10^-3 ( 0,29 %), donc C.

menu