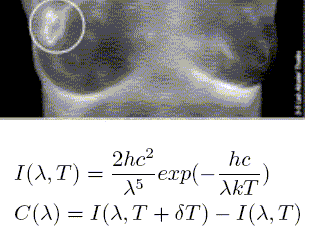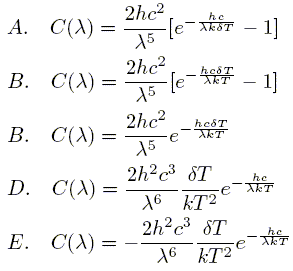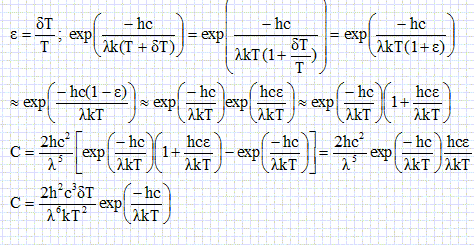QCM physique ( laser et cornée, bouteille et cloche de plongée, détection infrarouge d'un cancer du sein ) : concours médecine.

Laser et cornée. On peut corriger la courbure de la cornée en l’abrasant par laser. Le laser prototype Mark-III fonctionne en infra-rouge et utilise des séries d’impulsions très brèves, de durée Δti = 1 ps = 10-12 s et d’énergie Ei = 1 μJ par impulsion. Elles sont envoyées toutes les θ = 350 ps pendant une durée τ = 6 μs. Les séries de 6 μs se répètent avec une période p = (1/30) s. On considère le faisceau lumineux homogène et cylindrique, de rayon R = 50 μm. Il arrive perpendiculairement sur la cornée. On néglige l’absorption dans l’air et la réflexion partielle à la surface de la cornée. 1. Calculer la puissance moyenne Pi d’une impulsion. Cocher la ou les propositions vraies : A. Pi = Δti Ei ; B. Pi =Ei / Δti ; C. Pi = 10-18 W ; D. Pi = 106 W ; E. Pi = 106 J. énergie ( J) / durée (s) =10-6 / 10-12 = 106 W ( watt) ; donc D. 2. Calculer la puissance moyenne PL du laser sur période p ou plus. Cocher la ou les propositions vraies: A. PL = p Ei / (τ Δti) ; B. PL = p Δti Ei / τ ; C. PL = τ Ei / (p θ) ; D. PL = 5.6 109 W ; E. PL = 0.51 W. Energie mise en jeu pendant  t = 6 µs : nombre d'impulsions : t / q =  6 / 350 10-6 =1,714 104. Energie correspondante : Ei t / q =1,714 104 µJ. La fréquence des séries de 6 µs est f = 30 Hz ( 30  séries par seconde) Energie mise en jeu en 1s :  Ei t / (q p)=1,714 104 *30 =5,1 105 µJ s-1= 0,51 W donc C et E. 3. Exprimer l’intensité lumineuse I0 qui atteint la cornée pendant une impulsion. Cocher la proposition vraie : A. I0 = R Pi ;  B. I0 = π R2 Pi ;  C. I0 = Pi / R ; D. I0 = Pi / (π R2) ; E. aucune des expressions précédentes n’est vraie. Puissance d'une impulsion divisée par la section du faisceau cylindrique ; donc D. 4. Calculer I0. Cocher la proposition vraie : A. I0 = 7.9 10-27 W m-2 ; B. I0 = 1.3 10-10 W m-2 ; C. I0 = 7.9 10-3 W m-2 ; D. I0 = 1.3 1014 W m-2 ; E. I0 = 2 1015 W m-2. Section du faisceau : 3,14 *(50 10-6)2 =3,14*25 10-10 m2. I0 =106 / (3,14*25 10-10 ) = 1.3 1014 W m-2 , donc D. La cornée absorbe l’onde lumineuse avec une longueur d’absorption L = 4.9 μm. Elle a une masse volumique ρ = 1300 kg/m3 et une capacité calorifique massique C = 4000 J kg-1 K-1. L’énergie absorbée élève la température de la cornée. Des petites bulles, de rayon r = 1 μm, apparaissent à la surface de la cornée au bout d’un certain temps d’exposition par vaporisation “explosive” de la cornée lorsque la température atteint T = 302°C. La cornée avait une température initiale T0 = 37°C avant l’opération. On étudie la pénétration d’une impulsion laser dans un petit volume cylindrique de rayon r et d’épaisseur 2r. 5. Exprimer l’intensité lumineuse I(2r) présente à la profondeur 2r sous la surface de la cornée. Cocher la ou les propositions vraies : A. l’intensité lumineuse diminue avec la profondeur r ; B. I(2r) = 2r I0 /L ; C. I(2r) = I0 (2r/L)2 ; D. I(2r) = I0 e2r / L ; E. I(2r) = I0 e-2r / L. Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme :  I = I0 exp (-µx) I0 : flux  incident ; I : flux  sortant ; µ = 1/L coefficient d'atténuation linéique du milieu ; x = 2r : épaisseur du milieu traversé. 6. Exprimer l’intensité absorbée Iabs dans cette couche d’épaisseur 2r. On supposera 2r/L << 1. Cocher la proposition vraie : A. Iabs = 2r I0 /L ; B. Iabs = - 2r I0 /L ; C. Iabs = I0 (1 - 2r/L) ; D. Iabs = I0 (1 - 2r/L)2 ; E. Iabs =I0 - e-2r / L. Iabs = I0 -I(2r)=I0 (1- e-2r / L  ) ~I0 (1-( 1-2r / L) )~I0 2r / L, donc A. 7. Exprimer l’énergie Eabs absorbée dans le petit volume cylindrique. Cocher la ou les propositions vraies : A. Eabs = π L2 Iabs Δti ; B. Eabs = π r2 Iabs Δti ;  C. Eabs = π r2 Iabs / Δti ; D. Eabs = 4π r3 Ei / 3 ; E. Eabs = 4π r3 Pi Δti / 3 énergie (J) = puissance (W) * durée de l'impulsion (s) ; puissance (W) = intensité absorbée (W m-2 ) * section cylindrique de rayon r (m2) ; donc B. 8. Calculer l’accroissement de température ΔT correspondant à ce dépôt d’énergie. On donne (1.3 × π × 4.9)-1 = 0.05. Cocher la ou les propositions vraies : A. ΔT = 3 Eabs / (4π r3 ρ C) ; B. ΔT = Eabs / (2π r3 ρ C) ; C. ΔT = Ei / (πR2 ρ L C) ;  D. ΔT = 5 K ; E. ΔT = 10 K. Eabs  = masse de cornée absorbant l'impulsion * capacité thermique massique de la cornée (J kg-1 K-1) * différence de température K ou °C ). masse de la cornée = volume du cylindre de rayon r, de haureur 2r * masse volumique de la cornée. m =p r2 *2r r = 2 p r3 r ; Eabs  = 2 p r3 r C DT, donc B. Eabs = π r2 Iabs Δti   ; Pi =Ei / Δti ;  Pi =pR2 I0 d'où : Eabs = π r2 Iabs Ei / Pi =  π r2 Iabs Ei / (pR2 I0) = 2 p r3 r C DT ;  Iabs Ei / (pR2 I0) = 2  r r C DT ; or Iabs = 2r I0 /L d'où : Ei / (pR2 )=r C DT L, donc C. DT  = Ei / (πR2 ρ L C) =10-6 / (3,14 *2,5 10-9 *1300*4000*4,9 10-6) ~5 K, donc D. Calculer le nombre N d’impulsions nécessaires pour provoquer l’apparition d’une bulle. Cochez la ou les propositions vraies : A. N = Eabs / Ei ;  B. N = T / ΔT ;  C. N = (T-T0) / ΔT ; D. N = 115 ; E. N = 53. (302-37) / 5 =53. Calculer la durée dt d’intervention correspondante. Cocher la ou les propositions vraies : A. dt = N θ ; B. dt = N τ ; C. dt = N p ; D. dt = 19 ns ; E. dt = 0.69 ms. Les séries d'impulsions sont envoyées toutes les θ = 350 ps ; dt = N θ = 53*350 10-12 ~1,9 10-8 s ~19 ns. Bouteille de plongée. L’air dans les conditions normales de pression p et de température T contient 20% d’oxygène en volume. On note nair le nombre de moles d’air et nO2 et nN2 les nombres de moles d’oxygène et d’azote de l’air. On note pO2 et pN2 les pressions partielles d’oxygène et d’azote de l’air. 1. Cocher la ou les propositions vraies : A. Sous les conditions normales, l’oxygène de l’air occuperait un volume V02 = nO2 RT / (nair p) B. Sous les conditions normales, l’air occupe un volume Vair = nair RT / p ; C. nO2/nair = 0.2 D. nO2/nN2 = 0.25 ; E. pN2/pair = nair/nN2. Loi des gaz parfaits appliquée à l'air : pVair = nair RT, donc B. nO2/nair =0,2 ( 20% en volume, donc 20 % en moles ), donc C. nO2/nN2 = 0.25 =(nO2/nair ) / (nN2/nair )=0,2 / 0,8 = 1/4 = 0,25, donc D. pO2  =nO2/nair p ; pN2  =nN2/nair p ; pN2  / p = nN2/nair ; V02 = nO2 RT /  pO2    =  nO2 RT nair /( nO2p) = RT nair /p.   2. On dispose d’oxygène pur pour enrichir en oxygène une bouteille contenant nair moles d’air. Combien doit-on ajouter de moles n’O2 d’oxygène pur pour que la pression partielle de l’oxygène dans la bouteille soit de 50%, à température constante ? Cocher la proposition vraie : A. n’O2 = 0.2 nair ; B. n’O2 = 0.6 nair  ;  C. n’O2 = 2 nair ; D. n’O2 = 5 nair ; E. aucune des réponses précédentes n’est vraie. pression partielle de O2 = fraction molaire de O2 * pression p ; pression partielle de O2 / p = 0,5.  fraction molaire de O2  = (0,2 nair +n’O2 ) / (nair+n’O2 )  =0,5 ; 0,2 nair +n’O2 = 0,5  nair +0,5 n’O2 ;   n’O2 =0,6  nair , donc B. Cloche de plongée. Une cloche de plongée est constituée d’une cuve cylindrique, de section S = 1 m2 et de hauteur H = 2 m, ouverte vers le bas. Initialement, le bas de la cloche effleure tout juste la surface de l’eau. On note patm la pression atmosphérique et g ≈ 10 m s-2 l’accélération de la pesanteur. On descend la cloche dans l’eau de masse volumique ρ = 1000 kg m-3. Le haut de la cloche descend à la profondeur D et l’eau monte dans la cuve d’une hauteur h. On considère l’air emprisonné dans la cloche comme un gaz parfait. Sa température T = 15°C ne varie pas pendant la descente. 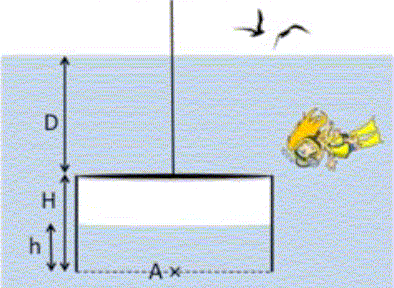1. Exprimer la pression au point A situé au bas de la cloche. Cocher la proposition vraie : A. pA = patm + ρgh ; B. pA = patm- ρgh ; C. pA = patm + ρg(D+H) ; D. pA = patm - ρg(D+H) ; E. pA = patm + ρg(D+h) La pression en A est égale à la pression atmosphérique augmentée de la pression due à la colonne d'eau de hauteur H+D. pA = patm + ρg(D+H), donc C. 2. Exprimer la pression p de l’air emprisonné dans la cloche en plongée à la profondeur D. Cocher la proposition vraie : A. p = patm ; B. p = pA + ρgh ;  C. p = pA - ρgh ; D. p = patm + ρgD ; E. p = patm + ρg(D+H-h). La pression de l'air est identique en tous points sous la cloche ; pA -p = rgh, donc C. pression à la surface air eau sous la cloche = pression atmosphérique + pression exercée par une colonne d'eau de hauteur H+D-h, donc E. 3. Cocher la ou les propositions vraies concernant l’air emprisonné dans la cloche : A. il subit une compression adiabatique selon la loi pVγ = constante. B. il subit une compression isotherme ;  C. il subit une dilatation isotherme ; D. il a reçu de l’énergie ; E. il a fourni un travail moteur. Le volume de l'air diminue, la température et la quantité de matière d'air restent constantes.  La pression de l'air emprisonné sous la cloche va augmenter. Donc B, compression isotherme. L'air reçoit de l'énergie, donc D. 4. On étudie la pression p de l’air emprisonné au cours de la descente. Cocher la ou les propositions vraies : A. p augmente pendant la descente vrai. B. p diminue pendant la descente C. p = patm h / (H-h) ; D. p = patm H / (H-h) ; E. p = RT / (SH). p = patm + ρg(D+H-h) ; pVair = constante ; initialement ce produit vaut :  patm S H ; finalement, il vaut : p S (H-h) , d'où patm  H = p  (H-h), donc D. 5. Calculer la profondeur D à laquelle on peut descendre le haut de la cloche pour que la hauteur d’eau dans la cuve ne dépasse pas h = 1 m. Cocher la proposition vraie : A. D = 10 m ; B. D = 9 m ; C. D = 8 m ; D. D = 5 m ; E. D = 2 m. patm  H = p  (H-h) ;  p = patm + ρg(D+H-h) ; patm  H /((H-h)) =patm + ρg(D+H-h) 105*2/(2-1) =105 +1000*10(D+2-1) ; 105 = 104 (D+1) ; D+1 = 10 m ; D = 9 m ; donc B. 6. On étudie le travail W des forces de pression de l’air emprisonné pendant la descente de la cloche. Cocher la ou les propositions vraies : A. W > 0 ; B. W < 0 ; C. |W| = 100 kJ ; D. |W| = 140 kJ ; E. |W| = 200 kJ. dW = -pdV avec patm Vinitial = p Vfinal = nRT = Constante ; pV = constante dW = -constante dV / V = -patm Vinitial d ln V ; intégrer : W = -patm Vinitial ln ( Vfinal /Vinitial ) Vfinal <Vinitial  donc   ln ( Vfinal /Vinitial ) <0 et W >0 ( A). W =  -patm SH ln ( Sh / (SH)) = -patm SH ln ( h / H) =-105*1*2 ln (1/2) = 1,4 105 J = 140 kJ, donc D. Détection infrarouge d'un cancer du sein.. L’image infrarouge, prise à 8 μm de longueur d’onde, montre le rayonnement thermique émis (dit de corps noir) par une patiente. Le codage de gris sur l’image va du plus sombre au plus clair pour une intensité lumineuse croissante. La région de surbrillance encerclée correspond à une tumeur. Les seins de la patiente ont une température moyenne T = 35°C. La tumeur présente un écart de température |δT| =2°C en valeur absolue. On la considère comme sphérique, de rayon r. On note σ la constante de Stefan-Boltzmann. L’intensité lumineuse I(λ,T) du rayonnement thermique émis à la longueur d’onde λ par un corps à la température T s’exprime, dans le cas présent, selon : On définit le contraste C(λ) de l’image au niveau de la tumeur comme : 1. Calculer la longueur d’onde λmax du maximum d’intensité lumineuse thermique de la partie saine du sein de la patiente. Cocher la proposition vraie : A. λmax = 1.1 μm ; B. λmax = 9.4 μm ; C. λmax = 16.6 μm ; D. λmax = 82.9 μm ; E. λmax= 146 μm. lmaxi .T = 2,9.10-3 m.K (loi de Wien) ; T = 273+35 = 308 K.  lmax =2,9.10-3 / 308 =9,4 10-6 m = 9,4 µm, donc B.   2. Exprimer la puissance lumineuse Pt de la tumeur. Cochez la ou les propositions vraies : A. Pt s’exprime en W ( vrai ) ; B. Pt s’exprime en W m-2 ; C. Pt = σ T4 ; D. Pt = π r2 σ T4 ; E. Pt = 4π r2 σ T4. Aire d'une sphère de rayon r : 4pr2 ; P = s T4 (loi de Stephan ) ; P s'exprime en Wm-2 ; s= 5,67 10-8 Wm-2K-4. Pt = P *Aire d'une sphère de rayon r = 4pr2 s T4, donc E. Calculer l’accroissement relatif de puissance lumineuse entre la tumeur et la même surface sphérique de rayon r dans une partie saine du sein. Cocher la ou les propositions vraies : A. δP/P = 0.64 % ; B. δP/P = 2.6 % ; C. δP/P = 22.9 % D. La tumeur est plus chaude que le sein normal E. La tumeur est plus froide que le sein normal.. (Ptumeur -Psain) /Psain = (T4tumeur -T4sain) / T4 sain =(Ttumeur  / Tsain )4-1 =(310/308)4-1 =2,6 10-2 ( 2,6 %), donc B. Exprimer le contraste C(λ) en fonction de λ, T et δT en faisant les approximations nécessaires. Cocher la proposition vraie : donc D. Calculer la longueur d’onde Λmax qui présente un maximum de contraste. On donne hc / (kT) = 47 μm. Cocher la proposition vraie : A. Λmax = 7.8 μm ; B. Λmax = 18.8 μm ; C. Λmax = 47 μm ; D. Λmax = 235 μm ; E. Λmax = 282 μm.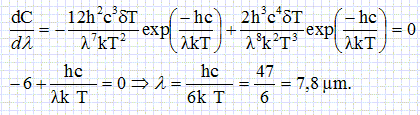

menu