Ressort vertical.
On considère un ressort fixé au plafond et dont les caractéristiques sont : longueur à vide L0 et constante de raideur k. Celui-ci est donc positionée verticalement. Un objet de masse m est fixé à son extrémité.
Effectuer un schéma du dispositif à vide et celui à l'équilibre.
Indiquer les grandeurs utiles. L'axe verticale Oz sera vertical orienté
vers le bas ; l'origine de l'axe est l'extrémité fixe du ressort. Les
forces seront représentées. Déterminer la longueur du ressort à l'équilibre, notée Léq.
On
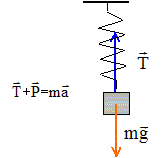
étudie le système { masse fixée au ressort }; le systéme est soumis à
son poids et à une force de rappel exercée par le ressort.
poids : vertical, vers le bas,
appliqué au centre d'inertie, valeur :
mg
tension du ressort : verticale,
dirigée vers la position
d'équilibre, appliquée au point de
fixation masse ressort, valeur proportionnelle
à la déformation du ressort.
 |
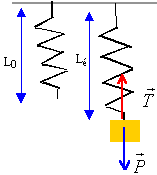
à l'équilibre : mg =
k(Léq-L0)
Léq = L0 + mg / k. |
|
Evaluer l'énergie potentielle élastique du système à la position d'équilibre.
L'énergie potentielle est définie à une constante près.
Si on choisit l'origine de l'énergie potentielle pour le ressort non déformé :
Ep = ½(Léq-L0)2.
Si on choisit l'origine de l'énergie potentielle pour le ressort à la position d'équilibre : Ep = 0. On fait ce choix car l'étude est simplifiée.
|
On effectue une élongation du ressort et de l'objet, élongation du ressort notée L1 avec L1 > L0. A l'instant t=0, l'objet est lâché sans vitesse initiale. L'objet oscille autour de cette position d'équilibre.
Déterminer l'équation en z caractérisant les oscillations et indiquer l'expression de la pulsation w0.
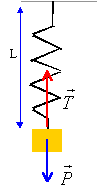
Ecarté de sa position
d'équilibre le ressort oscille : L=
Léq +x ; écrire la seconde loi de Newton sur un axe vertical dirigé vers le bas dont l'origine est à la position d'équilibre.
mg-k(L-l0)= m
d²x/dt² ; mg-k( Léq
+x-l0)= m d²x/dt² ; mg-k( Léq -l0) -
kx =m d²x/dt² ; or mg =
k(Léq-L0).
m
d²x/dt² + k x=0
(1)
Pulsation
w0
( rad s-1) : w0
= [k/m]½ d'où
l'écriture de (1) : d²x/dt² +
w20
x = 0 ou x"
+w20
x =0.
(1)
Quelle
est la variation d'énergie potentielle de pesanteur lorsque l'altitude
du centre d'inertie de l'objet passe de la position Léq à L1 ?
On choisit la position d'équilibre comme origine de l'énergie potentielle de pesanteur.
DEpp = Epp(L1)-Epp(Léq) = mg(L1 - Léq).
On attache sous l'objet de masse m, un second ressort identique au
premier, verticalement et fixé sur le plancher. L'écartement entre le
plancher et le plafond est 2L.
Le système est l'objet de masse m.
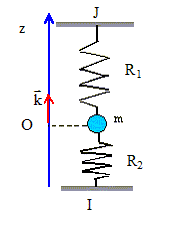
Représenter et donner l'expression des forces qui s'appliquent sur le système à l'équilibre.
|
On note l1 et l2 les
longueurs respectives de R1 et
R2.
l01 et l02 sont les
longueurs à vide. On note D=IJ= 2L. Le pendule
ainsi constitué peut osciller dans un plan
vertical sans frottement.
Etude
statique.
A l'équilibre, la cote de la masse m
coincîde avec l'origine de l'axe.
Les grandeurs vectorielles sont
écrites en gras et en bleu.
La masse est au repos.
R1 étiré a tendance à
être rappelé vers sa position à vide :
(l1-l01) >0
et T1
dirigée vers le haut.
R2 comprimé a tendance à
être rappelé vers sa position à vide :
(l2-l02) <0
et T2
dirigée vers le haut.
T1 =
k1(l1-l01)
k ;
T2 =
k2(l02-l2)k.
|
 |
Ecrire la condition vectorielle
d'équilibre.
k1(l1
éq-l01)
+ k2(l02-l2
éq) = mg ;
m =
[ k1(l1
éq-l01) +
k2(l02-l2
éq)] / g.
(1)
|
Etude d'un circuit LC.
On considère un condensateur de capacité C, alimenté par un générateur idéal de tension ( intensité délivrée constante I0 ). Le condensateur est initialement déchargé.
Faire le schéma de l'association électrique et déterminer l'expression littérale de la tension uc(t) aux bornes du condensateur.
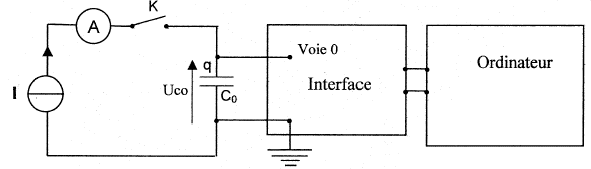
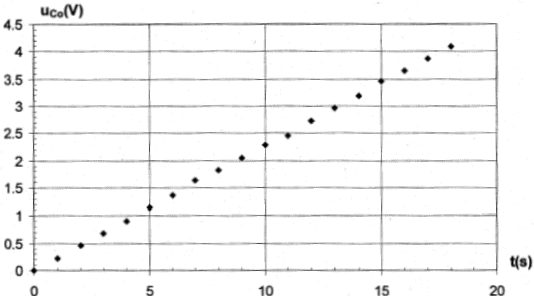
q= It ; charge en coulomb, intensité en
ampère et temps en seconde.
uc=q/C0= I/C0t droite de
coefficient directeur I/C0.
On considère une bobine parfaite ( inductance L ) alimmentée par
un générateur idéal de tension ( fem E ). Le courant traversant
initialement la bobine est nul. Faire le schéma de l'association et déterminer l'expression littérale i(t) du courant traversant la bobine.
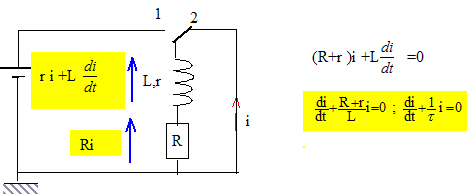
Solution de l'équation
différentielle du type i (t)= A
exp(-t/t) avec
t = L/(R+r).
La conservation de l'énergie
entraîne la continuité de
l'intensité.
La valeur de l'intensité à t=0 est
égale à valeur de l'intensité
en régime permanent lorsque l'interrupteur
était en position 1 :
i0= E/(R+r) à t=0.
D'où A = E/(R+r)
et i(t)
=E/(R+r)exp(-t/t).
|
On
considère un circuit oscillant LC dans lequel la bobine est idéale. Le
condensateur est initialement chargé sous une tension U telle que
q(t=0) = Q. Indiquer l'unité de Q dans le système internationnal.
Une charge électrique s'exprime en coulomb ( symbole C ).
Faire le schéma du circuit en indiquant les grandeurs utiles.
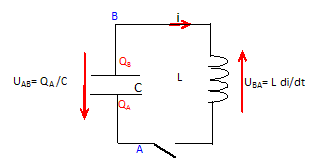
Montrer que l'équation différentielle de la charge q du condensateur est q" +w02q = 0. Quelle est l'expression de q(t) ?
uAB + uBA = 0 ; qA est notée q ; q /C + L di /dt =0 avec i = dq/dt et di/dt = d2q/dt2 = q".
Lq" + q/C = 0 soit q" + 1/(LC) q = 0 ; on pose w02 = 1/(LC).
Solution de cette équation différentielle : q(t) = A cos (w0t+ B) où A et B sont des constantes.
q(t=0) = Q =A cos B d'où B = 0 si Q est positive. et A = Q : q(t) = Q cos (w0t).
Quelle est l'expression de l'intensité du courant i(t) traversant le circuit ?
i(t) = dq/dt = -Qw0 sin(w0t).
|
A partir de l'oscillogramme représentant la tension uc aux bornes du condensateur et de la valeur L = 1,2 H, déterminer :
La période propre T0 des oscillations et leur fréquence f0.
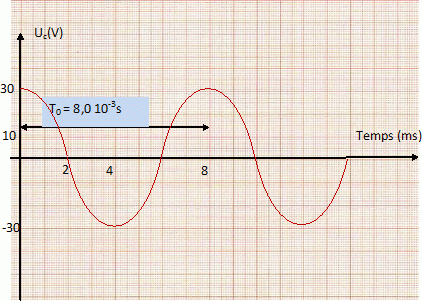
f0 = 1 /T0 = 1000 / 8 = 125 Hz.
La valeur de la capacité C du condensateur.
T0 = 2 p(LC)½ ; C = (T0 / 2 p)2 / L =(8 10-3 / 6,28)2 / 1,2 =1,352 10-6 F ~1,4 µF.
La charge initiale Q et la valeur de l'intensité maximale Imax.
Q= CUmax = 1,352 10-6 *30 =4,056 10-5 C ~ 4,1 10-5 C.
q(t) = Q cos (w0t) ; i(t) = dq/dt = -Qw0 sin (w0t) ; Imax = Qw0 =Q 2pf0 =4,056 10-5 *6,28*125 =3,2 10-2 A.
|









