Concours kiné Assas 2011 : mécanique : rotation de deux solides, forces électriques.

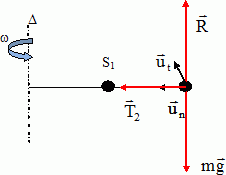
~Deux solides ponctuels S1 et S2 de même masse m, peuvent glisser sans frottement le long d'une tige horizontale ayant un mouvement de rotation uniforme de vitesse angulaire w autour d'un axe fixe vertical D. Les deux solides sont attachés par des fils inextensibles de masse négligeable, parallèles à la tige. Le fil 1 entre D et S1 et le fil 2 entre S1 et S2 sont identiques et ont une longueur L. 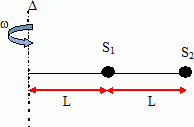Etude du solide S2. Donner la nature du mouvement de S2 et les caractéristiques de sont vecteur accélération. Exprimer ce dernier dans la base de Frenet en fonction des données. S2 est animé d'un mouvement circulaire uniforme à la vitesse angulaire w. L'accélération est horizontale, centripète, de valeur 2Lw2. 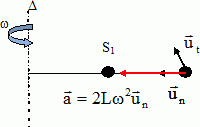Quelles sont les forces appliquées à S2 ? Les représenter. Le poids de S2, vertical, vers le bas, valeur mg  L'action de la tige, opposée au poids et la tension du fil T2. Quelle est l'expression littérale de la norme T2 de la tension du fil 2. Ecrire la seconde loi de Newton : 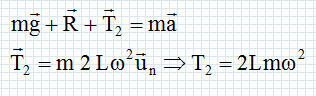Etude du solide S1. Exprimer le vecteur accélération  de S1 dans la base de Frenet en fonction des données. S1 est animé d'un mouvement circulaire uniforme à la vitesse angulaire w. L'accélération est horizontale, centripète, de valeur Lw2. 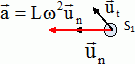Quelles sont les forces appliquées à S2 ? Les représenter. Le poids de S1, vertical, vers le bas, valeur mg  L'action de la tige, opposée au poids et les tensions des fils T1 et T2. 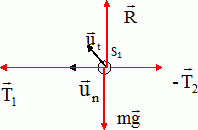Quelle est l'expression littérale de T1 ? Ecrire la seconde loi de Newton : 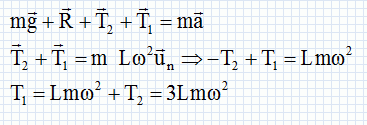Calculer le rapport des normes des deux tensions. T1/T2 = 1,5. Vitesse angulaire maximale. On augmente progressivement la vitesse angulaire w du système. Sachant que la tension maximale T0 que peut supporter les fils est 1,0 N, quel fil casse le premier et pour quelle valeur de w exprimée en tr min-1. On donne : m = 40 g ; L = 20 cm ; g = 10 m s-2. T1 étant supérieure à T2, le fil 1 casse le premier dès que : T1 = T0 = 1,0 = 3 m L w2. w2= T0 / (3mL) ; w = [T0 / (3mL)]½ =[1,0 / (3*0,040*0,20)]½ =( 1 / 2,4 10-2)½ =(200/2,4)½ ~6,46 rad /s. w = 6,46 *60 /(2*3,14)=62 tr min-1. 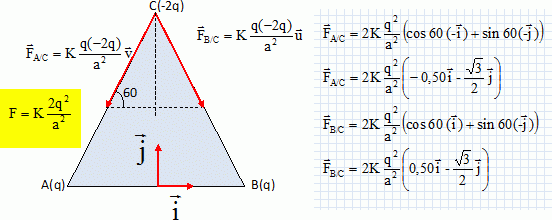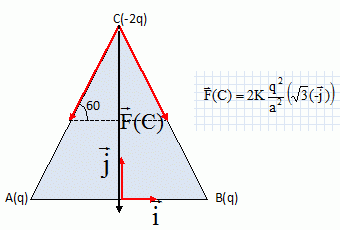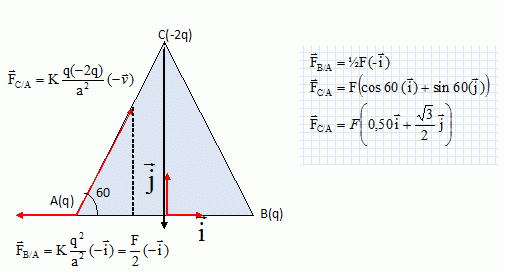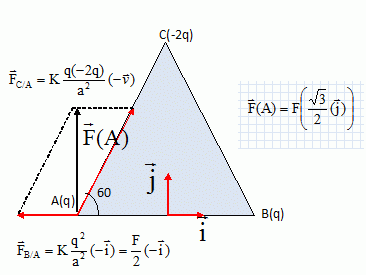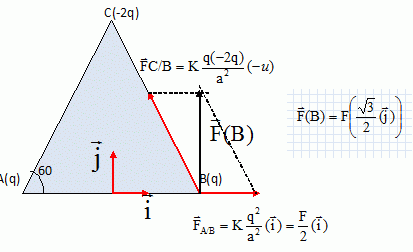Forces électriques. On dispose de trois charges électriques ponctuelles qA, qB, qC placées aux sommets d'un triangle équilatéral de côté a. qA =qB= q positif ; qC = -2q négative. K = 1 / (4pe0) avec e0 la permittivité du vide. AB = AC = BC = a. La force électrique exercée par qA sur qB est notée FA/B. La force électrique exercée par qC sur qB est notée FC/B.... La résultante des forces électriques exercées sur B est notée F(B). La résultante des forces électriques exercées sur A est notée F(A).... Etude des forces électriques s'exerçant sur C. Montrer que les forces FA/C et FB/C ont une norme commune que l'on notera F. Exprimer F en fonction de q et a. Représenter ces forces. 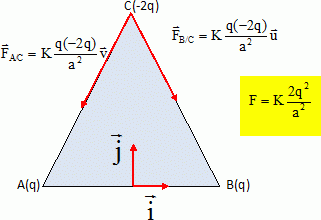Exprimer les composantes de ces vecteurs dans la base ( i, j ). En déduire l'expression  de F(C)  que l'on représentera. Etude des forces électriques s'exerçant sur A. Exprimer les normes FB/A et FC/A des vecteurs correspondants en fonction de F. Exprimer les composantes de ces vecteurs dans la base ( i, j ). En déduire l'expression  de F(A)  que l'on représentera. Etude des forces s'exerçant sur B. Par un argument simple déduire l'expression de F(B) et représenter ce vecteur. Par raison de symétrie par rapport à la hauteur du triangle issue de C.

menu