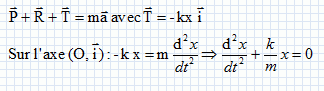Etude d'un oscillateur mécanique : concours orthoptie Toulouse 2011.

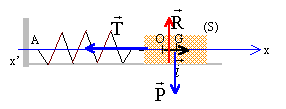
On considère un ressort horizontal et de raideur k. l'extrémité A du ressort est fixe. Un solide S, de masse m, est accroché à l'autre extrémité du ressort et se déplace sans frottement sur un banc horizontal. La masse du ressort est négligeable devant m. On étudie le mouvement du centre d'inertie G du solide, dans le référentiel du laboratoire considéré comme galiléen. On repère la position de G par son abscisse x sur une axe horizontal x'x d'origine O. Le point O correspond à la projection de G à l'équilibre. Dessiner un schéma de cet oscillateur mécanique en faisant apparaître les forces auxquelles le point G est soumis. Préciser la nature de ces forces. Le solide S est soumis à  : son poids, vertical, vers le bas, valeur mg - à l'action du rail, vertical, vers le haut, valeur mg - à une force de rappel exercée par le ressort, proportionnelle à l'allongement. Etablir l'équation différentielle admettant x(t) comme solution. Ecrire la seconde loi de Newton : En déduire la pulsation propre w0 en fonction des caractéristiques de l'oscillateur.   w0 =(k/m)½.  Montrer que une solution de l'équation différentielle précédente peut s'écrire sous la forme : x(t) = Xm cos (2pt/T0 + F0). Xm : amplitude du mouvement et F0 phase à l'origine des dates. Dériver deux fois par rapport au temps : x'(t) = -Xm 2 pi / T0 sin (2pt/T0 + F0) ; x"(t) = -Xm 4 pi2 / T02 cos(2pt/T0 + F0). Repport dans l'équation différentielle : [-Xm 4 pi2 / T02 cos (2pt/T0 + F0) ] + k / mXm cos (2pt/T0 + F0) = 0 Xm cos (2pt/T0 + F0) [ k / m -4 pi2 / T02 ] = 0 Or 4 pi2 / T02 = k / m : cette égalité est bien vérifiée quel que soit le temps. En déduire l'expression littérale de la coordonnée vx du vecteur vitesse du point G en fonction du temps. vx = dx/dt = -Xm 2 pi / T0 sin (2pt/T0 + F0). Donner les expressions littérales de l'abscisse x(0) et de la coordonnée vx(0) à l'origine des dates. x(0) = Xm cos ( F0). vx (0)= -Xm 2 pi / T0 sin ( F0)= -Xmw0 sin ( F0). .

menu