Le corps humain simulé par des résistances ou par un dipole RC : concours orthoptie Toulouse 2011.

Dans sa modélisation la plus simple le corps humain peut être modélisé par quelques résistances. 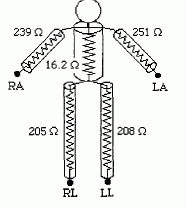En effet, s'il existe un gradient de potentiel électrique dans un conducteur, un courant électrique apparaît dans le milieu traduisant la rupture d'un équilibre. La relation qui lie la densité de courant J au champ électrique E dépend de la conductivité du milieu : c'est la loi d'Ohm locale ( J = s E ) où entre deux points M1 et M2 : où dl est équivalent à un déplacement dx selon la direction ex entre M1 et M2 et pù n est le vecteur normal au point M1 ici. On connaît plus la loi d'Ohm macroscopique où l'on définit la résistance qui lie la tension et l'intensité. Cette loi s'écrit U = RI mais la valeur de R peut être parfois complexe à calculer. Néanmoins si on considère que le conducteur est un cylindre de section S et de longueur L entre les points M1 et M2, sa formule est assez simple car R = U/I. Donner dans le cas d'un conducteur cylindrique la formule permettant de calculer la résistance en fonction de s, L et S. U = E L ; I = J S et J = s E. Par suite : I = s E S et R = U/I = s L/ ( s  S). s : conductivité ( S m-1) ; L : longueur (m) ; S : section (m2); R résistance (ohm W) Cette formule simple fut utilisée dans la création des premiers fusibles qui étaitent constitués d'un simple fil de cuivre. En utilisant la formule précédente, calculer la résistance d'un fil de 50 cm de long et de 1 mm2 de section, où 1/s = 1,7 10-8 W m. L =0,50 m ; S = 1 10-6 m2 ; R = 1,7 10-8 * 0,50 / 1 10-6 = 8,5 10-3 W. Si on applique une tension de 12 V, calculer le courant qui circule dans le fil.   I = U/R = 12 / 8,5 10-3 =1,4 103 A.  Calculer la puissance thermique dissipée par le fil dans ce cas. La puissance thermique est égale à la puissance dissipée par effet Joule : RI2 = U2/R =122 / 8,5 10-3 =1,7 104 W = 17 kW. Commenter. Le fil n'est pas capable de dissiper une telle puissance dans le milieu extérieur. La température du fil va s'élever jusqu'à atteindre  la fusion du métal. En conséquence le circuit électrique sera ouvert. Ce fil de cuivre joue bien le rôle de fusible. 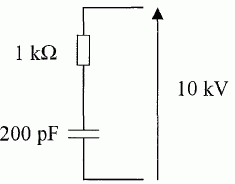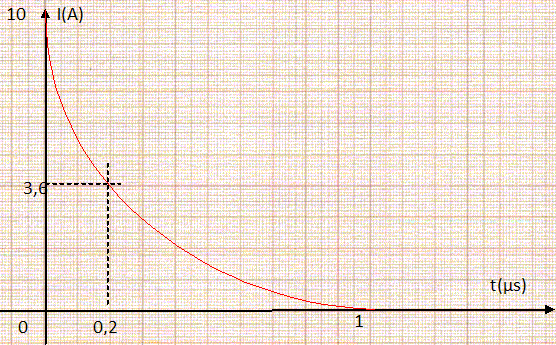Le corps humain simulé par un circuit RC. 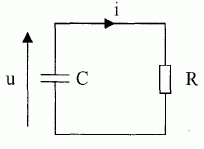Montrer que i(t) satisfait à l'équation différentielle i + RCdi/dt =0. 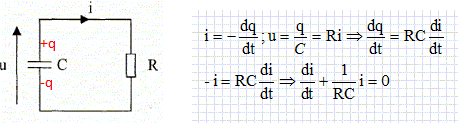Vérifier que i(t) = I0 exp(-t/(RC)) est solution de cette équation différentielle. On note U0 la valeur de la tension à l'instant t=0. di/dt = -1/(RC) I0 exp(-t/(RC)) ; repport dans l'équation différentielle -1/(RC) I0 exp(-t/(RC)) +1/(RC)I0 exp(-t/(RC)) =0  est bien vérifiée quel que soit le temps. Exprimer I0 en fonction de U0. 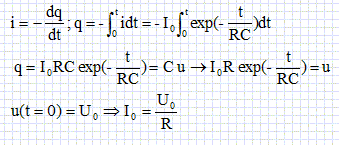Le corps humain est souvent simulé par un circuit RC. Modélisons le corps humain par un condensateur chargé de capacité C = 200 pF en série avec une résistance R = 1 kW tel que : Le corps humain chargé est le siège d'une différence de potentielle proche de 10kV. Calculer le courant maximal pouvant le parcourir dans de telles conditions. L'intensté du courant pase par une valeur extrème au tout début de la décharge du condensateur dans la résistance R. I0 =104 / 103 = 10 A. Calculer la constante de temps en µs. t = RC = 103 *200 10-12 =2 10-7 s = 0,2 µs. Tracer l'allure du courant de décharge et commenter. Les conséquences dues au passage du courant dans le corps humain dépendent de deux facteurs, la valeur de l'intensité maximale et la durée du passage. Dans ce cas, l'intensité s'annule au bout d'une microseconde. Il n'y a donc aucun danger.

menu