|
Charges
d'un condensateur, mouvement sur un plan incliné :
concours Orthoptie Toulouse 2010 |
|||||||
|
|||||||
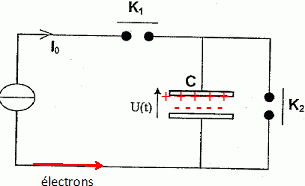
 I0 = 2 µA ; C = 3 mF. A l'instant t=0, on ferme l'interrupteur K1. Indiquer par un schéma simple la nature et le sens du déplacement des porteurs de charge. Préciser la polarité des armatures et la nature des porteurs de charges. Dans les conducteurs métalliques, les électrons se déplacent. Les électrons se déplacent en sens contraire du sens conventionnel du courant.
On note q la charge positive de l'armature supérieure. L'intensité étant constante, q = I0t. De plus U(t) = q / C = I0/C t. Quelle sera la tension théorique U(t) au bout de 2,5 min après fermeture de K1 ? 2,5 min = 150 s ; C = 3 10-3 F ; I0 = 2 10-6 A. U(2,5) = 2 10-6 / 3 10-3 *150 = 2 10-3 *50 = 0,1 V. Quelle serait la forme de U(t) si on le traçait sur un graphique où l'on mettait le temps en abscisse et U(t) en ordonnée ? U(t) = I0/C t = 2 10-6 / 3 10-3 t = 2/3 10-3 t. C'est l'équation d'une droite passant par l'origine. Calculer la puissance instantanée P (2,5 min) reçue pat le condensateur. Puissance = U(t) I0 = I20/C t = (2 10-6)2 / 3 10-3 *150 =2 10-7 W.
Calculer l'énergie emmagasinée par le condensateur, 2,5 min après la fermeture de K1. E = ½CU2(2,5) =0,5 *3 10-3 *0,12 =1,5 10-5 J. 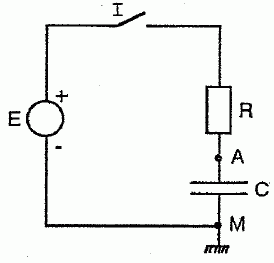 Un dipôle (RC) peut être relié, en fermant l'interrupteur I , à un générateur de tension continue E. On donne R = 3 kW ; C = 10 µF ; E = 5 V. On mesure la différence de potentiel VA-VM entre les points A et M ( masse ). A l'instant t=0, on ferme l'interrupteur. Au bout de combien de temps le condensateur est-il chargé à 99 % ? Au bout d'une durée égale à 5 fois la constante de temps t = RC. t = 5 RC =5 *3 103 *10 10-6 =0,15 s. Représenter sur un graphique, l'allure approximative de VA-VM à partir de t=0. Montrer sur ce même graphique comment l'on peut déterminer la valeur de la constante de temps t. 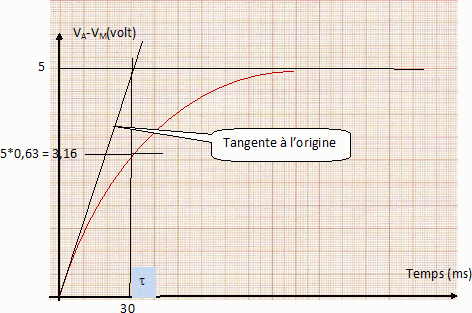
Mouvement sans frottement sur un plan incliné. On donne g = 9,8 m s-2. Sur un plan incliné d'un angle a = 45° par rapport à l'horizontale, on lâche en un point O, sans vitesse initiale, un corps de masse m. Soit A un point tel que L=OA =2,0 m. Ecrire la relation de la dynamique pour le centre d'inertie du corps en explicitant les termes. 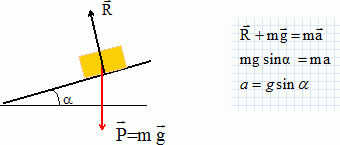 R : action du plan, perpendiculaire au support ; P : poids ( N) ; m : mass (kg) ; a : accélération (m s-2). Ecrire la loi horaire du mouvement. La vitesse est une primitive de l'accélération. Sur un axe parallèle au plan, dirigé vers le bas du plan ( origine de l'axe, la position de départ à t=0 ) : v(t) = g sin a t + Cste. La constante d'intégration est déterminée par les conditions initiales. v(0) = 0 = Cste. La position est une primitive de la vitesse : x = ½g sin a t2 + Cste. La constante d'intégration est déterminée par les conditions initiales. x(0) = 0 = Cste. x = ½g sin a t2 = 0,5 *9,8 sin 45 t2 =3,5 t2.
|
|||||||
| |
|||||||
|
|