Saut à l'élastique : concours Orthoptie Nantes  2010

Un sexagénaire, qui n'a pas froid aux yeux, de masse m, de centre d'inertie G, s'essaie au saut à l'élastique. La longueur de l'élastique est L. Attaché à l'élastique par les pieds ( point M ), debout sur la plateforme, il se laisse tomber sans vitesse initiale et voyage tête en bas. L'élastique non tendu possède une longueur L0. Pour OM < L0, L = L0, l'intensité de la tension de l'élastique est égale à zéro car on néglige la masse de l'élastique. Pour une longueur OM > L0, OM=L, l'élastique tendu est caractérisé par  une constante de raideur k ( Nm-1 ). On admet que le centre de gravité G de la personne a un mouvement vertical d'axe Oz orienté vers le bas. On néglige toutes les forces de frottement. m = 70 kg ; g = 10 m s-2 ; k = 100 N m-1 ; L0 = 18 m ; MG = 1 m. 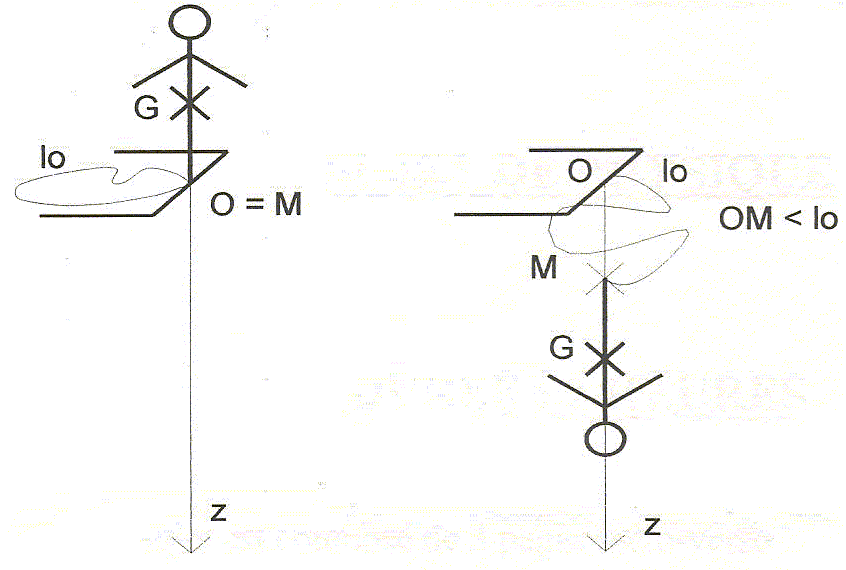OM < L0. Etablir l'équation que doit satisfaire z = OG.En déduire l'évolution temporelle z(t). Le sauteur n'est soumis qu'à son poids : il s'agit d'une chute libre sans vitesse initiale. Ecrire la seconde loi de Newton sur l'axe Oz : g = a. La vitesse est une primitive de l'accélération ; la constante d'intégration est nulle, la vitesse initiale étant nulle. v = gt = 10 t. La position est une primitive de la vitesse : z(t) = ½gt2 + Cste. z(0) = OG = -1 m ; z(t) = ½gt2 -1 ;  z(t) = 5 t2-1.     Exprimer puis calculer le temps t1 au bout duquel l'élastique devient tendu. z(t1) =L0 = 5 t12-1 ; t1 = ( (L0+1) / 5 )½ =(19/5)½ =1,949 ~1,9 s. Quelle est la vitesse du sauteur à cet instant ? v(t1) = 10 t1 = 19 m /s. OM >L0. Déterminer l'équation du mouvement en z. 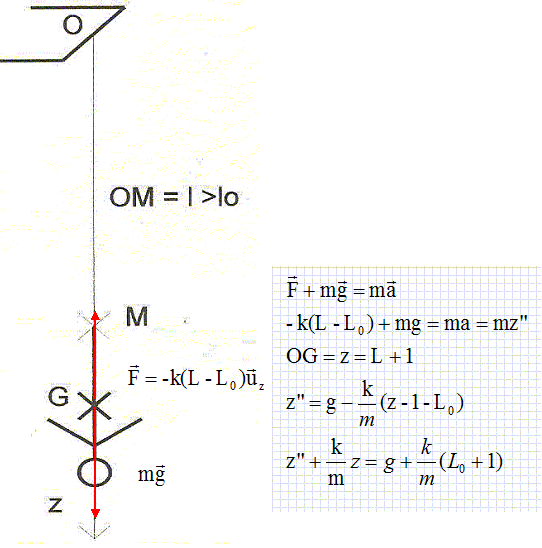Pour quelle valeur de z =z1, la chute commence-t-elle à être freinée ? Exprimer z1 en fonction de m, g, k MG et L0. Calculer z1. z" = 0 ;  z1 = L0+MG +mg / k= 19 +70*10/100 = 26 m. Montrer que z(t) s'écrit z(t) = z1 +z0 (cos( wt+j). Exprimer w en fonction de k et m. Calculer w. Solution générale de z" +k/m z = 0 ; on pose w2 = k/m ; w =(k/m)½ =(100 / 70)½ =1,195 ~1,2 rad/s. z(t) = z0 cos(wt+j) avec z0 et j des constantes. Solution particulière de l'équation différentielle :  z1 = L0+1 +mg/k. Solution générale de l'équation différentielle : z(t) = z0 cos(wt+j) +z1. A t=t1 ; z(t1) = L0+1 = 19= z0 cos(wt1+j) + 26 ; -7 =z0 cos(1,2*1,9+j) ; -7 =z0 cos(2,33+j) ; vitesse z'((t1) =19,49 = -z0w  sin(wt1+j) ; 19,49 = -1,195z0  sin(2,33+j) ; z0 sin(2,33+j) = -16,31. tan (2,33+j) = 16,31 /7 = 2,33 ; 2,33+j =1,165 ; j = -1,165 rad ou + 1,165 rad. La vitesse z'((t1) étant positive, on retient j = -1,165 rad. Par suite z0 = -7 / cos(2,33+j)  = -17,7 m. z(t) = -17,7 cos (1,2 t -1,165 ) +26. Sachant que la nouvelle origine des dates t'=0 est choisie à l'instant t1, donner la relation reliant z0, cos j, m, g et k puis la relation reliant w, z0, sin j, g et t1. z(t1) =L0 +1= z0 cos(wt1+j) +z1 ; or wt1=-2j ;  z0 cos(-j) +z1 ;  z1 = L0+1 +mg/k ;  L0 +1= z0 cos(j) + L0+1 +mg/k ; z0 cos(j) +mg / k =0. Dériver z(t) par rapport au temps : v(t1) = -z0 w sin(wt1+j) ; v(t1) =g t1 = -z0 w sin(-j) ;  g t1 = z0 w sin(j). Exprimer l'énergie mécanique du sauteur à z = z1. En déduire l'expression de la vitesse maximale vmax en fonction de z1, g, GM, k, m et L0. Calculer vmax. EM = Ec + Ep. On choisit l'origine de l'énergie potentielle en z=L0+1. L'énergie mécanique initiale est sous forme potentielle de pesanteur EM(t=0) =  mg(L0+2). L'énergie mécanique  est sous forme cinétique, potentielle de pesanteur et potentielle élastique en z = z1. EM =½mv2 +mg ( -z1+L0+1) +½k( z1-L0-1)2. L'énergie mécanique se conserve en l'absence de frottements : ½mv2 +mg ( z1-L0-1) +½k( z1-L0-1)2 = mg(L0+2). ½mvmax2 = -mg ( -z1+L0+1) -½k( z1-L0-1)2 + mg(L0+2). vmax2 = -2g ( -z1+L0+1) -k / m( z1-L0-1)2 + 2g(L0+2). vmax =[ -2g ( -z1+L0+1) -k / m( z1-L0-1)2 + 2g(L0+2)]½. vmax =[ -20 ( 19-26) -100/70( 26-19)2 + 20(18+2)]½ = (+140 -70 +400)½ =21,7 ~22 m/s. Avec une étude énergétique similaire, établir l'équation du second degré permettant de déterminer zmax ( le calcul de zmax n'est pas demandé ). L'énergie mécanique  est sous forme  potentielle de pesanteur et potentielle élastique en z = zmax. EM = mg ( -zmax+L0+1) +½k( zmax-L0-1)2. L'énergie mécanique se conserve en l'absence de frottements : mg ( -zmax+L0+1) +½k( zmax-L0-1)2 = mg(L0+2). Pour t = t'2, l'élastique n'est plus tendu. Quelle est la nature du mouvement du sauteur ? Le sauteur n'est soumis qu'à son poids, si l'élastique n'est pas tendu. Il s'agit d'une chute libre verticale avec vitesse initiale. A quelle hauteur doit remonter le sauteur dans les hypothèses du texte ? L'énergie mécanique étant constante, le sauteur remonte jusqu'à sa position initiale. En réalité,les frottements ne sont pas négligeables et le sauteur finit par s'immobiliser à la position OG = zfinal.. Déterminer zfinal. Le sauteur immobile est en l'équilibre sous l'action de son poids et de la tension du ressort. mg = k(L-L0) avec zfinal = L+1 ; mg / k = zfinal -1-L0 ; zfinal = mg / k +1+L0 = z1 = 26 m. Qu'elle est l'énergie mécanique perdue lors du saut ? Qu'est-elle devenue ? L'énergie mécanique initiale est sous forme potentielle de pesanteur EM(t=0) =  mg(L0+2). L'énergie mécanique finale est sous forme potentielle de pesanteur et sous forme potentielle élastique :  EM(t=fin) =  mg(-zfinal +1+L0)+ ½l(zfinal -1-L0)2. Diminution d'énergie mécanique : EM(t=fin)- EM(t=0) =mg(-zfinal +1+L0)+ ½l(zfinal -1-L0)2  - mg(L0+2). EM(t=fin)- EM(t=0) =700( -26+19) +50*49 -700*20 = -1,6 104 J. L'énergie mécanique perdue est convertie en énergie thermique..

menu