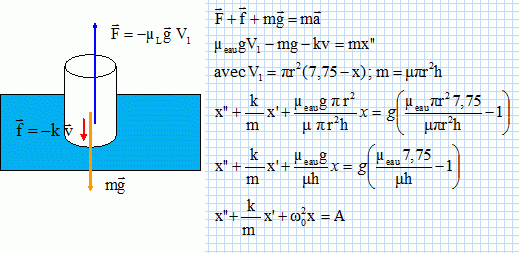|
Radioactivité,
le radon 222 ; oscillations à la surface de l'eau :
concours Orthoptie Rennes 2010 |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
Définir l'isotopie et donner un exemple concret. Deux isotopes ne se différencient que par leurs nombres de neutrons ; ils ont le même numéro atomique Z. 126C ; 136C ; 146C. Donner la composition du noyau de radon 222. Z = 86 ; 86 protons et 222-86 = 136 neutrons. Le radon 222 est issu du noyau de radium 226 Ecrire l'équation de cette désintégration. De quel type de radioactivité s'agit-il ? 22688Ra ---> 22286Rn + 42He, radioactivité de type alpha. Donner les deux autres types de radioactivité en précisant le nom de la particule émise. Radioactivité de type ß- : émission d'un électron. Radioactivité de type ß+ : émission d'un positon. Ecrire l'équation de désintégration du radon 222. 22286Rn ---> 21884Po+ 42He. Au cours de la désintégration du radon 222, on observe l'émission d'un rayonnement g. Définir cette émission. Quel noyau émet ce rayonnement ? Le rayonnement g est un photon, de même nature que la lumière, mais beaucoup plus énergétique. Le noyau fils 21884Po, se trouve souvent dans un état excité : lors du retour à l'état fondamental, il libère son surplus d'énergie sous forme de photon g.
On considère un échantillon
contenant à la date t=0, N0 = 1000 noyaux de radon 222. N = 0,01 N0 = N0 exp(-lt1) avec l = ln2 / 3,8 = 0,1824 jour-1. ln 0,01 = -0,1824 t1 ; t1 = 25,2 ~ 25 jours. Définir l'unité le becquerel, donner son symbol. L'activité, nombre de désintégraions par seconde, s'exprime en becquerel ( Bq). Calculer l'activité de l'échantillon à la date t1. N (t1) = 0,01 N0 = 10 noyaux. A(t1 ) = l N (t1) = 2,1112 10-6* 10 = 2,1 10-5 Bq. En l'absence de ventillation, l'air d'une maison a une concentration constante en radon 222. Expliquer pourquoi, dans certains endroits, la concentration en radon 222 reste constante au cours du temps. Dans un endroit peut ventilé, situé dans une région granitique, le radon 222 se forme par une succession de désintégrations radioactives ; d'autre part le radon est lui même radioactif, il se désintègre en polonium 218. Expliquer le principe de la datation pour une espèce radioactive. De toutes les méthodes radio-chronologiques ( basées sur la loi statistique de Curie-Rutherford-Soddy ou loi de décroissance radioactive), celle de la datation au carbone 14 est la plus connue. Dans la haute atmosphère, soumis au rayonnement cosmique galactique constitué de protons, des neutrons secondaires interagissent avec les noyaux d'azote 14. Cette réaction forme un isotope AZX du carbone : le fameux carbone 14. Immédiatement formé le carbone 14 s'oxyde en se combinant avec l'oxygène pour former du dioxyde de carbone qui se mélange avec le reste de l'atmosphère. Or le carbone 14 est radioactif. La teneur en carbone 14 est constante dans le monde ( dans l'atmosphère comme dans chaque organisme vivant ). Cela est du à un équilibre entre la désintégration et la production de carbone 14. Chaque gramme de carbone contient des atomes de carbone 14. On enregistre en moyenne 13,5 désintégrations par minute et par gramme de carbone. Lorsqu'un arbre, par exemple, est abattu, le bois cesse de vivre, le processus de photosynthèse s'arrête et il n'y a plus d'absorption de dioxyde de carbone. Le carbone 14 est alors libre de se désintégrer sans compensation. On peut donc dater l'âge de la mort de l'organisme ( au moment où cesse tout échange de CO2 avec l'atmosphère). La mesure de la concentration en radon 222 dans l'air des poumons d'une personne décédée dans un tel lieu, permettrait-elle de connaîte précisément la date du décès ? Oui si le décès n'est pas antétieur à 5 demi-vie radioactive du radon 222 ( soit environ 19 jours). Au delà, il reste trop peu de raddon 222 dans les poumons. Calculer en J et en MeV, l'énergie libérée par la désintégration d'un noyau de radon 222. Dm = m(21884Po) + m(42He) - m(22286Rn) = 217,9629 + 4,002 - 221,9704 = -0,0055 u -0,0055 * 1,66054 10-27 = -9,13297 10-30 kg ; E = | Dm|c2 = 9,13297 10-30* (3,00 108 )2 =8,22 10-13 J. 8,22 10-13 / 1,60 10-13 = 5,14 MeV.
Oscillations à la surface de l'eau. On étudie un bouchon de forme cylindrique, de rayon r = 2,00 cm et de hauteur h = 10,0 cm. Le bouchon est homogène de masse volumique µ =750 kg m-3. Dans tout l'exercice on suppose que le bouchon reste vertical. On repère son cente de gravité par l'abscisse x. L'axe Ox étant vertical dirigé vers le haut. On donne g = 9,81 m s-2. Dans cette partie, on place le bouchon dans un liquide de masse volumique µL. Le bouchon est immobile et flotte. Faire un bilan des forces s'exerçant sur le bouchon et les faire figurer sur un schéma sans souci d'échelle. Le bouchon est soumis à son poids , vertical, vers le bas, valeur mg et à la poussée d'Archimède, verticale, vers le haut, égale au poids du volume de liquide déplacé. 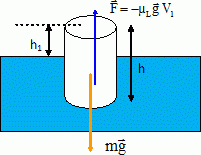 La partie émergée ( hors de l'eau ) du bouchon représente une hauteur h1 = 2,25 cm. Exprimer µL en fonction de µ, h et h1. Calculer µL. V = p r2 h ; m = µV = µp r2 h ; P = mg = µ p r2 hg. V1 = p r2 (h-h1 ); F = µLgV1 = µL p r2 (h-h1 ) g. A l'équilibre, les forces se compensent : µ p r2 hg = µL p r2 (h-h1 ) g. µ h = µL (h-h1 ) ; µL = µ h /(h-h1 ) = 750 *10 / 7,75 = 968 kg m-3. Dans cette partie le bouchon n'est plus immobile. On l'immerge verticalement dans l'eau de masse volumique µeau = 1000 kg m-3. A la date t=0, on l'enfonce de façon à ce qu'il ne reste plus qu'un centimètre hors de l'eau et on le lâche sans vitesse initiale. L'origine de l'axe, x=0, correspond au centre de gravité dans la position d'équilibre. Déterminer la valeur X0 de x à la date t=0. Le bouchon est enfoncé de 1,25 cm : X0 = - 1,25 cm. Pour une position quelconque, déterminer l'expression de la poussée d'Archimède exercée par l'eau sur le bouchon en fonction de x. Hauteur immergée : ½h +2,75 -x = 5+2,75-x = 7,75 - x cm = (7,75-x ) 10-2 m. Volume immergé : p r2 (7,75-x ) 10-2 ; poussée : µeau p r2 (7,75-x ) 10-2 g. On néglige les frottements. Montrer que l'équation différentielle peut se mettre sous la forme x" +w02x = A où w0 et A sont des constantes. Poids mg avec m = µ p r2 h. Ecrire la seconde loi de Newton sur l'axe Ox : -µ p r2 h g +µeau p r2 (7,75-x ) g = m x" = µ p r2 h x". -µ h g +µeau (7,75-x ) g = µ h x". x" + µeau / (µ h) g x =( 7,75 µeau / ( µ h) -1 ) g. On pose w02 =µeau / (µ h) g = 1000 *9,81 / (750*0,1) =130,8 rad2 s-2. On pose A = ( 7,75 µeau / ( µ h) -1 ) g = (7,75*1000/ (750*10)-1)*9,81 =0,327 m s-2.
|
|||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||
|
|
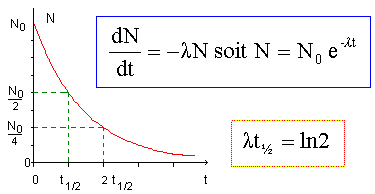
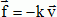d'équilibre