Aurélie 28/11/10
 

 

Charge et décharge d'un condensateur : concours technicien météo 2010



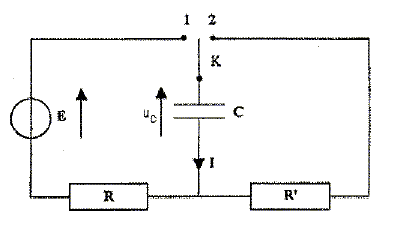On étudie la chare et la décharge d'un condensateur à travers un conducteur ohmique.On réalise le montage suivant :

Le condensateur est initialement déchargé et à la date t=0, on bascule l'interrupteur en position 1.
On donne R= 2,2 kW ; C = 4,7 µF ; R' = 10 kW.
Etablir l'équation différentielle E = RC duc/dt +uc vérifiée par la tension uc aux bornes du condensateur pendant la phase de charge.
Additivité des tensions : E = Ri + uc.
i = dq/dt et q =C uc d'où : i = C duc/dt.
Par suite : E = RC duc/dt +uc.
La solution de cette équation est de la forme : uc(t) = A(1-exp(-at)).
Exprimer A et a en fonction de E, R et C.
Au bout d'un temps assez long, le condensateur est chargé, il se comporte comme un interrupteur ouvert : l'intensité est nulle et la tension aux bornes du condensateur est égale à E.
u( infini) = E = A(1-0) d'où A = E.
i(t) = Cduc/dt =  EC (a) exp(-at).
A l'instant t=0, le condensateur non chargé se comporte comme un interrupteur fermé, uc(0) = 0 ; par suite i(0) = E/R.
i(0) =E/R =  EC (a) d'où a = 1/(RC).
A partir du graphe 1, déterminer la valeur de E.

 

La méthode d'Euler permet de calculer, pas à pas, les valeurs de uc(t) et de duc(t)/dt à intervalles de temps réguliers choisis Dt. Si Dt est choisi suffisamment petit dans le cadre de l'expérience, on peut écrire :
uc(t +Dt) = uc(t) + [duc/dt]t Dt. On choisit Dt = 1 ms.
A l'aide de l'équation différentielle, déterminer la valeur initiale de la dérivée notée [duc/dt]0.
E = RC  [duc/dt]0 +uc(0). Or uc(0) = 0, condensateur non chargé.
[duc/dt]0  = E / (RC) = 5 / (2,2 103 *4,7 10-6) =483,6~4,8 102 V s-1.
En appliquant la méthode d'Euler, compléter le tableau suivant :

t(ms)
 0
 1
 2
 3
uc(t)
 0
 0,48
 0,92
 1,3
[duc/dt]t 4,8 102 4,4 102 3,9 102 3,6 102

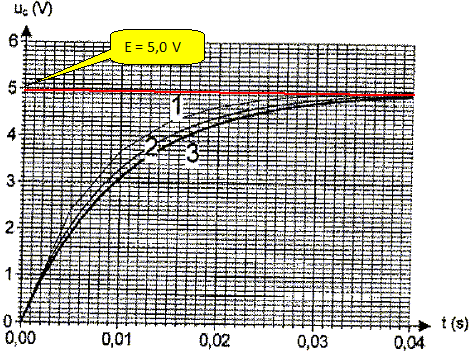
uc(1) = uc(0) + [duc/dt]0 Dt = 0 +483,6*0,001 =0,4836 ~0,48 V.
[duc/dt]1 = (E- uc(1)) / (RC) = (5-0,4836) / (2,2 103 *4,7 10-6) =436,8 V s-1.
uc(2) = uc(1) + [duc/dt]1 Dt = 0,4836 +436,8*0,001 =0,9204 ~0,92 V.
[duc/dt]2 = (E- uc(2)) / (RC) = (5-0,92) / (2,2 103 *4,7 10-6) =394,6 V s-1.
uc(3) = uc(2) + [duc/dt]2 Dt = 0,92 +394,6*0,001 =1,315 ~1,3 V.
[duc/dt]3 = (E- uc(3)) / (RC) = (5-1,315) / (2,2 103 *4,7 10-6) =356,4 V s-1.
Sur le graphe ci-dessus, on a représenté trois courbes :
- courbe n°1 : courbe obtenue par la méthode d'Euler avec un pas Dt = 5 ms.
- courbe n°2 : courbe obtenue par la méthode d'Euler avec un pas Dt = 2 ms.
- courbe n°3 : représentation  de la solution analytique de l'équation différentielle.
Quel est l'influence du pas Dt, utilisé dans la méthode d'Euler ?
Qu'entend-on par " si Dt est considéré comme suffisamment petit dans le cadre de l'expérience" ?
La courbe obtenue par la méthode d'Euler est confondue avec la courbe théorique si le pas est assez petit ( Dt doit être environ égal au dixième de la constante de temps RC  : RC /10 ~ 1 ms. )

Définir la constante de temps du circuit. La déterminer à partir du graphe 1 en explicitant la méthode ; en déduire une valeur expérimentale de C et la comparer à la valeur nominale.
La constante de temps t est la durée au bout de laquelle la tension uc(t) est égale à 63 % de sa valeur finale E.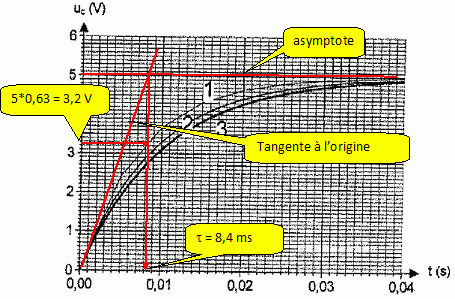

t = RC ; C = t / R = 8,4 10-3 / 2,2 103 = 3,8 10-6 F = 3,8 µF.
Ecart relatif : (4,7-3,8 ) / 4,7 = 0,19 ( 19 %).
Un travail identique à partir de la courbe 3 théorique donnerait de bien meilleur résultat.






On bascule l'interrupteur en position 2 lorsque le condensateur est chargé.
Exprimer, puis calculer la constante de temps t' du circuit lors de la décharge.
t'=R'C = 10 104 * 4,7 10-6 = 0,47 s.
Dessiner l'allure uc(t) lors de la décharge en indiquant sur le graphe les grandeurs caractéristiques : uc( début de décharge), uc( fin de décharge) et t'.





 





menu