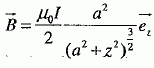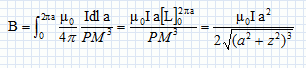Concours ITPE 2011 : Force centrale, gravimètre supraconducteur.

Que se passerait-il pour l'exploration spatiale si la force d'attraction entre deux corps était inversement proportionnelle à la distance entre eux ? Pour répondre à cette question, on étudie le mouvement d'un point matériel de masse m soumis de la part d'un point fixe O à la seule force attractive : 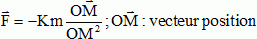; K désigne une constante positive.    Par application du théorème du moment cinétique, montrer que le mouvement du point M est plan.champ magnétique spire ligne de champ Le référentiel d'étude étant galiléen : La dérivée par rapport au temps du moment cinétique du point matériel M par rapport au point fixe O est égal au moment, par rapport à ce point, de la somme vectorielle des forces agissant sur le point matériel M . 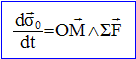Or les vecteurs force et position sont colinéaires, la dérivée du moment cinétique par rapport au temps est donc nulle : le moment cinétique est un vecteur constant. Le moment cinétique étant un vecteur constant, la trajectoire est plane, contenue dans un plan perpendiculaire au vecteur moment cinétique. En déduire une constante du mouvement sous la forme C = r2q' dans le système de coordonnées polaires. 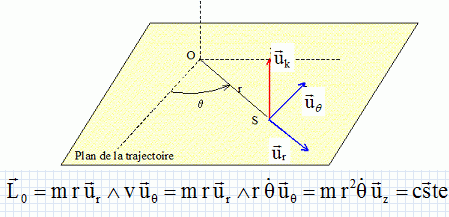Exprimer l'énergie mécanique du système. Montrer qu'elle constitue une constante du mouvement. L'énergie mécanique E est la somme de l'énergie cinétique et de l'énergie potentielle. 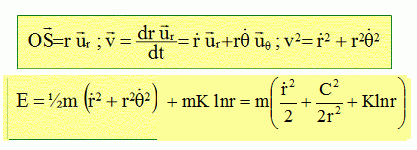Le point matériel est soumis à une force centrale conservative : cette force dérive de l'énergie potentielle K ln r. En conséquence l'énergie mécanique est constante. Montrer comment une étude graphique mettant en jeu la fonction f(r) = C2/(2r2) +K ln r permet de répondre à la question posée dans le titre de l'exercice. Le terme ½mr'² représente l'énergie cinétique d'une particule de masse m effectuant un mouvement suivant r : énergie cinétique radiale. Le terme f(r) = C2/(2r2) +K ln r est le terme d'énergie potentielle effective. Si r tend vers zéro, le terme C2/r2 croît plus vite que le terme K ln r décroît : f(r) tend vers l'infini. Si r tend vers l'infini, f(r) tend vers l'infini. f '(r) = -C2r'/r3 +Kr'/r =0 si r =C/ K½ : il s'agit d'un minimum. f(C/ K½) = ½K +K ln(C/ K½), peut être négatif si C2/K < 0,36. 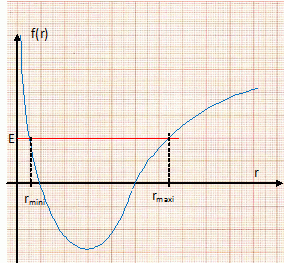Dans le puits de potentiel les états sont liés. La trajectoire est elliptique entre deux valeurs rmini et rmaxi. Si rmini = rmaxi , la trajectoire est un cercle. On pose u = 1/r. 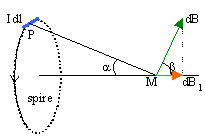Déterminer l'équation différentielle vérifiée par u(q). Dériver E par rapport au temps. L'énergie mécanique E étant constante, sa dérivée est nulle. r' r" -C2 r' / r3 + Kr'/r=0 ;  r" -C2 / r3 + K/r = 0 ; u = 1/r ; u' = - r' / r2 ; u" = -r" / r2 + 2r'2 / r3 d'où : r" =- u"r2+2r'2/r = -u"/u2 -2 u'2 / u3. -u"/u2 -2 u'2 / u3 -C2  u3 + Ku = 0 ; ......................................   Montrer qu'une orbite circulaire est possible et déterminer sa période en fonction de K et C. f '(r) = -C2r'/r3 +Kr'/r =0 si r =C/ K½ : il s'agit d'un minimum. L'orbite est circulaire. ............................................. Champ magnétique au voisinage d'un axe de révolution. On considère une spire conductrice (S), de rayon a et d'axe Oz, parcourue par un courant d'intensité I constante. On cherche à déterminer le champ magnétique créé par (S) en un point M de l'axe Oz, de côte z. Justifier précisément la direction du champ magnétique. L'élément de courant Idl crée en M , le champ élémentaire dB, perpendiculaire à PM, de module : Idl et PM étant perpendiculaire sin(q)=1. La régle de l'observateur d'Ampère donne la direction et le sens du champ. Par raison de symétrie le champ résultant sera porté par l'axe horizontal. La composante utile sera dBcos(b) = dBsin(a). Montrer que : Pour tous les éléments Idl, l'angle a et PM sont les mêmes. L'intégration de dB sur toute la spire donne le module du champ résultant ( sin a = rayon a / PM ). Représenter les lignes de champ magnétique dans un plan contenant l'axe Oz. Le champ magnétique est tangent en chaque points d'une ligne de champ. Les lignes de champ électromagnétique tournent autour des courants. 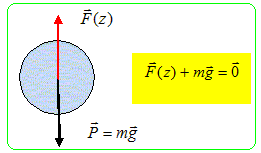Lévitation d'une sphère supraconductrice. On étudie, en régime permanent, l'action d'une bobine sur une sphère supraconductrice M, de masse m de rayon R. 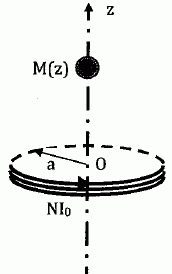La bobine est constituée de N spires circulaires, de rayon a, parcourue par un courant d'intensité I0 constante. Les spires sont très resserrées de sorte que le résultat obtenu ci-dessus reste valable en remplaçant I par NI0. On suppose que la sphère supraconductrice se situe sur l'axe de la bobine. On admet que l'énergie potentielle de la sphère, plongée dans le champ magnétique créé par la bobine est  donnée par : 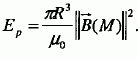Montrer que la force à laquelle est soumise la sphère se met sous la forme :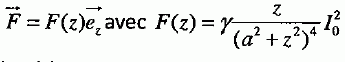et exprimer g . La force de « lévitation magnétique » résulte de l’action du champ magnétique, créé par la bobine parcourue par un courant permanent, sur les courants qui parcourent la sphère. La force F et le champ magnétique B ont la même symétrie. La force F dérive de l'énergie potentielle. 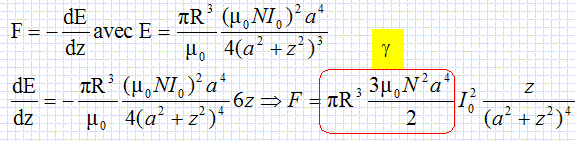Tracer l'allure de F(z) pour z >0. Ecrire la condition d'équilibre de la sphère. Montrer qualitativement qu'il existe une masse critique au delà de laquelle cette condition d'équilibre n'est pas satisfaite. Discuter  la stabilité des conditions d'équilibre. Stabilité des positions d’équilibre. On choisit un courant I0= 14 A. La figure suivante représente la fonction F(z) en fonction de z pour z variant de 0 à 10 cm. mg = 0,005*9,8 = 0,049 N position d’équilibre z1 : si z augmente à partir de z1, l’intensité de la force de lévitation dirigée vers le haut augmente ; or le poids dirigé vers le bas reste constant. La résultante des forces est dirigée vers le haut et tend à écarter la sphère de sa position d’équilibre z1. Cette position d’équilibre est instable. position d’équilibre z2 : si z augmente à partir de z2, l’intensité de la force de lévitation dirigée vers le haut diminue ; or le poids dirigé vers le bas reste constant. La résultante des forces est dirigée vers le bas et tend à ramener la sphère de sa position d’équilibre z2. Cette position d’équilibre est stable. .

menu