|
Concours
ITPE 2011 : thermodynamique du moteur Diesel. |
|||||||
|
|||||||
|
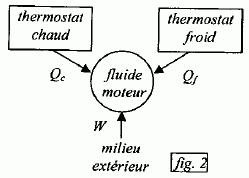
On considère un système matériel quelconque, pouvant échanger avec l'extérieur du travail W et de la chaleur Q. Rappeler la relation générale qui découle du premier principe de la thermodynamique reliant W et Q. La variation d'énergie interne est égale à : DU=W+Q. Cette variation est nulle si la machine effectue un cycle. Quelle inégalité déduit-on du second principe de la thermodynamique pour la variation DS de l'entropie d'un système mis en contact successifs avec différents thermostats de températures différentes Ti avec lesquels il échange des chaleurs Qi ? Que devient-elle si le système effectue un cycle ? 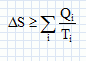 l'entropie est une fonction d'état, sa variation d'entropie est nulle sur un cycle. l'entropie est une fonction d'état, sa variation d'entropie est nulle sur un cycle.Soit g = Cpm / Cvm le rapport des capacités thermiques molaires d'un gaz parfait de pression P, de volume V et de température T. Ecrire la relation entre P et V lors d'une transformation adiabatique quasistatique ou réversible d'un gaz parfait, puis celle reliant T et V, et enfin entre P et T. 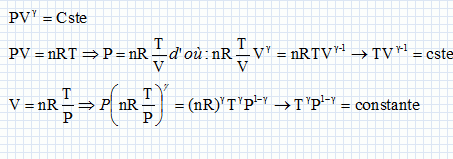 Quelle est la variation d'entropie du gaz lors de cette transformation ? L'entropie du gaz parfait ne varie pas lors d'une transformation adiabatique réversible. Cycle moteur ditherme théorique. On considère un système thermodynamique ( par exemple une masse donnée de fluide ) subissant un cycle moteur constituée de transformations successives quelconques au cours duquel il n'échange de la chaleur qu'avec deux thermostats ( chaleur Qf avec le thermostat froid à la température Tf ; chaleur Qc avec le thermostat chaud à la température Tc ) et du travail W avec le milieu extérieur. Conventionnellement, la chaleur et le travail échangés sont positifs s'ils sont absorbés par le système, et négatifs s'ils sont fournis par lui.
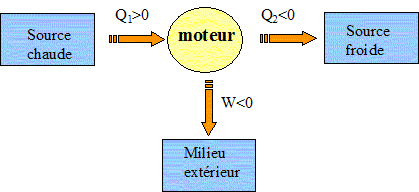
Le moteur fourni du travail W au milieu extérieur : W <0. Il reçoit de l'énergie à la source chaude Qc >0 ; il cède de l'énergie à la source froide : Qf <0 Rendement = énergie utile / énergie dépensée = |W| / Qc.
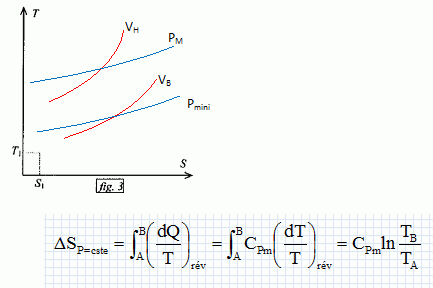
Exprimer h en fonction exclusive de Qf et Qc . Premier principe : W+Qf+Qc=0 soit W= -(Qf + Qc) h =| -(Qf + Qc)| / Qc = | -(Qf / Qc +1)| / Qc = 1+ Qf / Qc = 1- |Qf |/ Qc =avec Qf négatif. Montrer que h est toujours inférieur à une valeur limite que l'on déterminera en fonction des température Tf et Tc· Second principe : sur le cycle. 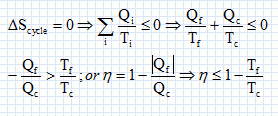 Le rendement est maximal dans le cas de la réversibilité et vaut h = 1-Tf/Tc. Modélisation du cycle moteur réel. On considère dans cette question un diagramme représentant la température ( ordonnée ) en fonction de l'entropie S ( abscisse ). Le moteur Diesel est construit d'après les contraintes mécaniques suivantes : - volume minimum de la chambre de combustion VH ; volume maximum de la chambre de combustion VB ; pression maximale tolérée PM ; température maximale tolérée TM. Le système thermodynamique subissant le cycle moteur est constitué du mélange { air, d'esence et produits de combustion } considéré comme un gaz parfait dont on supposera la quantité de matière n et les caractéristiques moyennes ( Cpm, Cvm, g ) constants par souci de simplicité. De même on néglige l'influence des phases { aspiration de l'air frais, refoulement des gaz d'échappement }. Sur un diagramme ( T, S), tracer qualitativement les deux courbes isochores V = VH et V = VB ( on justifiera brièvement leur allure ). Même question pour les isobares. Dans le cas d'un gaz parfait, pour une évolution réversible à volume constant : dQ=Cvm dT. 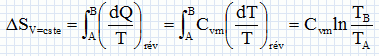
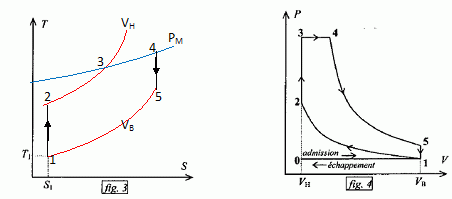 Expliquer pourquoi le diagramme ( T, S ) permet de visualiser directement le rendement du cycle dans le cas d'un fonctionnement réversible du moteur. Le diagramme (T, S) donne les valeurs de Tf et Tc, et par suite permet le calcul du rendement.
Paramètrage du cycle. Soient a = VB/VH le rapport volumétrique ; b = P3/P2, la surpression et r = V4/VH le rapport de surchauffe. Exprimer les chaleurs Q23 et Q34 fournies par la combustion du carburant en fonction de n, R, g, T2, T3 et T4. 1- 2 : compression adiabatique réversible donc Q12=0. 2- 3 : isochore : le travail échangé est nul ; la variation d'énergie interne du gaz est égal à Q23. L'énergie interne d'un gaz parfait ne dépend que de la température d'où Q23 = nCv,m (T3-T2) avec Cvm = R / (g-1). 3-4 : isobare réversible : la variation d'enthalpie est égale à Q34. Q34 = n Cp,m( T4-T3) avec Cpm = R g/ (g-1). 4-5 : détente adiabatique réversible donc Q45=0. 5-1 : détente isochore : le travail échangé est nul ; la variation d'énergie interne du gaz est égal à Q51. L'énergie interne d'un gaz parfait ne dépend que de la température d'où Q51 = nCv,m (T1-T5). Exprimer le rendement h en fonction uniquement des chaleurs des phases utiles du cycle. Travail fourni au cours du cycle : W énergie mise en jeu au cours du cycle : Q23 + Q34 + Q51. La variation d'énergie interne est nulle sur le cycle : W+Q23 + Q34 + Q51=0 -W = Q23 + Q34 + Q51 h= [Q23 + Q34 + Q51] / [Q23 + Q34] = 1+Q51 / [Q23 + Q34] Exprimer le rendement en fonction de g et des cinq températures T1 à T5 exclusivement. 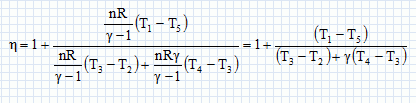 Exprimer T2 et P2 en fonction de P1 et T1 respectivement, et de a et g. La transformation 1-2 est adiabatique réversible. V1 = VB et V2 = VH. 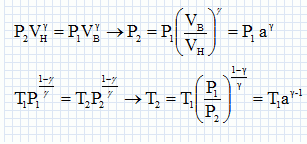 Exprimer T3 et T4 en fonction de T1, a, b, r et g. La transformation 2-3 est isochore d'où : P3/T3 =P2 / T2 soit P3/P2=T3/T2 =b. T3= bT2 = bT1 ag-1. La transformation 3-4 est isobare d'où : V3/T3=V4/T4 soit V4/V3=T4/T3 =T4/TH = r. T4= rT3 = rbT1 ag-1. Exprimer T5 en fonction de T1, b, r et g. La transformation 4-5 est adiabatique réversible : T5 V5g-1 = T4 V4g-1. La transformation 5-1 est isochore : V5 = V1 = VB soit T5 VBg-1 = T4 V4g-1. T5 = T4 [V4 /VB ]g-1. Or a = VB /VH ; r = V4 /VH d'où V4 /VB = r / b ; par suite : T5 = T4 [ r / a ]g-1 = rgbT1. En déduire l'expression du rendement : 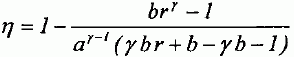 T1-T5 = T1[ 1-rgb] T3-T2 = bT1 ag-1-T1 ag-1 = T1[ b -1]ag-1. T4-T3 = rbT1 ag-1- bT1 ag-1 =T1[ r -1]bag-1. g(T4-T3) =T1[ r -1]gbag-1.
|
|||||||
| |
|||||||
|
|