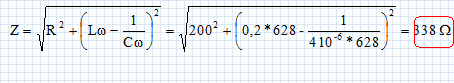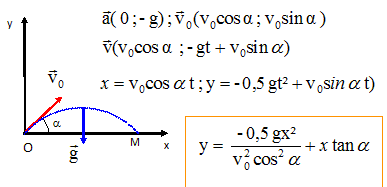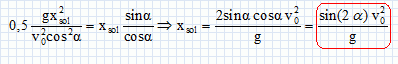Electricité, hydraulique, mécanique : concours ingénieur territorial 2011.

Circuit en régime sinuqoïdal et compensation. Une tension sinusoïdale de valeur efficace U = 20 V et de fréquence f = 100 Hz alimente un circuit RLC série ( R = 200 ohms ; L = 0,2 H ; C = 4 µF). Calculer l'impédance du circuit ainsi que le facteur de puissance. w = 2 p f = 2*3,14*100 = 628 rad/s. Facteur de puissance cos f = R/Z = 200 / 338 = 0,59. Danger!!!! .... deux solutions pour j +53,7 ou -53,7 1/Cw est supérieur à Lw donc j =-53,7. Calculer les puissances active, réactive et apparente. I = U / Z = 20 / 338 = 5,917 10-2 A. composant P : puissance active (W) Q : puissance réactive (var) R RI2 = 0,70 0 L 0 LwI²  =0,44 C 0 -I²/(Cw) = -1,39 total 0,70 -0,95 Autre méthode : P = UI cos f =20*0,05917*0,59 = 0,70 W. Q = UI sin f =20*0,05917*(-0,806) = -0,95 var. ( la tension est en retard sur l'intensité ). S = (P2+Q2)½ = 1,18 VA. On désire diminuer la puissance réactive consommée par le circuit par l'ajout d'un condensateur C'. Comment doit-on brancher C' ? Calculer la capacité C' pour une diminution de moitié de la puissance réactive. Il est parfois nécessaire d'augmenter le facteur de puissance cosj = P / S (donc diminuer j). Pour cela on branche généralement en dérivation un condensateur C' aux bornes du dipôle. La puissance active n'est pas modifiée par le branchement , en revanche la puissance réactive diminue de la quantité U²C'w. 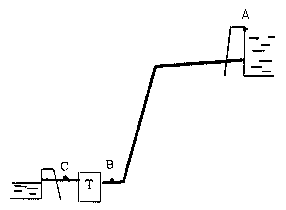La puissance réactive doit diminuer de ½Qinitial = 0,477 var. C' =½Q / (U2w) =0,477 / (202*628) =1,9 10-6 F = 1,9 µF. Hydraulique : étude du rendement d'un barrage. L'une des conduites forcées d'un barrage hydraulique, de diamètre d = 2 m, est reliée à une turbine Pelton. Le point haut du barrage est à une altitude h1 = 1450 m à la pression atmosphérique. L'entrée de la turbine est à l'altitude h2 = 632 m et à la pression P2. On négligera les pertes de charges. On donne : g = 9,81 m s-2 ; µeau = 1000 kg m-3 ; patm = 105 Pa ; débit volumique en B ( entrée turbine )  : 10 000 L/s. Déterminer la vitesse d'écoulement à l'entrée de la turbine. Section de la conduite S = p d2/4 = 3,14 m2. vitesse ( m/s) = débit ( m3/s ) / section ( m2) = 10 / 3,14 = 3,18 m/s. Calculer la pression à l'entrée de la turbine. Expression simplifiée de Bernoulli entre A(1) et B(2), (E21= 0) : ½ m (v12-v22) + m/r (p1-p2) + mg (z1-z2) = E21 s'écrit : ½ (v12-v22) + 1/r (p1-p2) + g (z1-z2) = 0. 1/r (p1-p2) = -[ ½ (v12-v22) + g (z1-z2)]. La surface du lac étant très grande, la vitesse de l'eau en A ( en 1) est négligeable. 1/r (p1-p2) = -[0,5(0-3,182) +9,81(1450-632)] = -[-5,07+8024,58]=-8065. p1-p2 = -1000*(-8065). p2 = p1+8,065 106 = 105 + 80,65 105 = 81,65 105 Pa ~ 82 bars. A la sortie de la turbine la vitesse de l'eau est négligeable et sa pression est égale à la pression atmosphérique. Calculer l'énergie fournie à la turbine pour chaque kilogramme d'eau.  ½ m (vB2-vC2) + m/r (pB-pC) + mg (zB-zC) = ECB masse m =1 kg ; zB=zC ; pC=105 Pa ; pB=81,65 105 Pa ; vB=3,18 m/s ; vC =0. 0,5*3,182+ 1/1000 *(81,65-1) 105 +0=EBC. EBC= 5,066+8065 = 8070 J /kg. En déduire la puissance fournie à la turbine. Débit massique (kg /s ) fois EBC (J/kg) = débit volumique (m3/s) * masse volumique ( kg /m3 ) *EBC (J/kg) P =10 000* 8070 = 8,07 107 W ~ 81 MW. La turbine a un rendement rturbine = 0,7. Elle est reliée au réseau électrique apr le biais d'un altrenateur de rendement ralternateur =0,92 et d'un transformateur de rendement rtransformateur = 0,95. Calculer la puissance électrique injectée sur le réseau électrique par le barrage. P rturbine ralternateur rtransformateur =8,07 107 *0,7*0,92*0,95 =4,94 107 W ~49 MW. Trajectoire d'une balle de golf. Un golfeur frappe une balle de golf de masse m, assimilée à une sphère de rayon r, lui communiquant une vitesse initiale v0 dans une direction qui fait un angle alpha avec l'horizontale. Déterminer la forme de la trajectoire du centre d'inertie de la balle. (l'action de l'air est négligeable). La balle soumise uniquement à son poids est en chute libre. Ecrire la seconde loi de Newton sur un axe verticale.   La trajectoire est une  parabole. Déterminer la distance entre le golfeur et le point d'impact de la balle. ( on considèrera que le golfeur est au niveau de la balle au moment de l'impact ). Au sol, y=0 : A.N : alpha = 40° ; v0 = 40 m/s ; g = 9,8 m s-2. xsol =sin 80 /9,8 * 402 ~161 m. Dans une seconde partie, le golfeur ne maitrise pas son geste et envoie la balle dans un étang. La balle de golf descend alors verticalement pour atteindre le fond de l'eau. On considèrera que l'eau exerce une force de frottement de sens opposé à celui de la vitesse et de valeur kf. Déterminer l'équation vérifiée par la vitesse de la balle. La balle est soumise à son poids, à la pousée d'Archimède et à une force de frottement. On note V le volume de la balle : m = reau V. Préciser l'expression de v(t), équation horaire de la vitesse de la balle. On donne r = 2 cm ; m = 50 g et k = 0,07 SI.  k/m =0,07 / 0,05 = 1,4 s-1. V = 4/3*3,14 0,023 =3,35 10-5 m3 ; rballe =m /V =0,05 / 3,35 10-5  =1492 kg m-3 ; 1-reau / rballe= 1-1 / 1,492 = 0,33. par suite dv/dt +1,4 v = 9,8*0,33 =3,24. (1) Solution particulière de (1) : vlimite = mg(1-reau / rballe) / k = 3,24 / 1,4 =2,3 m/s. Solution générale de dv/dt + k/m v = 0 : v(t) = A exp(-k/m t ) avec A une constante. Solution générale de (1) : v(t) =A exp(-k/m t ) + vlimite . La constante A est déterminée par la condition initiale, au moment où la balle arrive à la surface de l'eau. Cet instant est choisi comme origine des date. A + vlimite  = v(t=0). Lors de son parcours dans l'air, la balle n'est soumise qu'à son poids ; si on suppose que le point de départ de la balle est à la même altitude que la surface de l'eau, le théorème de l'énergie cinétique conduit à v(t=0) = v0. v(t=0) est inclinée d'un angle ß  = -a par rapport à l'orizontale. La valeur de la vitesse sur un axe vertical est alors : A =v0 sin a.

menu