|
Mesures de masse volumique : concours général 2011. |
||||||
|
||||||
|
Les atomes J. Perrin 1ère édition en 1913. .... comme pour une poudre insoluble ordinaire : on mesure les masses d'eau et d'émulsion qui remplissent un même flacon, puis, par dessication à l'étuve, la masse de résine suspendue dans l'émulsion. Cette dessication à 110 °C donne un liquide visqueux, qui ne perd plus de poids dans l'étuve et qui se solidifie à la tempérrature ordinaire en un verre transparent jaune. Donner un synonyme de dessication. Déshydratation. Comment ces mesures permettent-elles d'accéder à la densité de la matière qui forme les grains ? Densité par rapport à l'eau = masse d'un certain volume de résine / masse du même volume d'eau. Les mesures des masses d'eau et d'émulsion occupant le même volume donne la densité de l'émulsion. La densité par rapport à l'eau a même valeur que la masse volumique exprimée en g cm-3, des grains. Après dessication , on mesure la masse de résine ; on mesure également le volume de la résine : puis diviser la masse exprimée en gramme par le volume exprimé en mL. En quoi est-il essentiel que le liquide visqueux ne perdent plus de poids dans l'étuve ? Comment le vérifier ? Tant qu'il reste de l'eau ( déshydratation incomplète) le liquide visqueux perd du poids : effectuer des pesées régulières. On trouve dans un article des compte rendus de l'académie des Sciences ( 1908, tome CXLVI n°19 ) les données suivantes : "49,586 mL de cette émulsion contenait 49,373 g d'eau et 0,287 g de gomme-gutte". En ne supposant aucune contraction de volume lors de l'ajout, quel volume occupait l'eau contenue dans l'émulsion ? La masse volumique de l'eau étant 1,00 g / mL, le volume d'eau est égal à : 49,373 ~ 49,4 mL. En déduire la masse volumique µ de la gomme-gutte utilisée. Volume de la gomme-gutte = 49,586 -49,373 = 0,213 mL µ = 0,287 / 0,213 = 1,34742 ~1,35 g cm-3. Quelques mois plus tard et à l'occasion de son livre Les atomes, Jean Perrin donne, pour cette même masse volumique la valeur µ' = 1,1942 g cm-3. Proposer une explication pour cette différence. En quelques mois la gomme-gutte déshydratée a fixée la vapeur d'eau atmosphérique et forme une émulsion. Si on admet que le volume occupé par le liquide visqueux est inchangé, quelles modifications de la citation proposeriez-vous ? Justifier par un calcul. Volume du liquide visqueux inchangé : 0,213 mL ; masse de gomme-gutte inchangée : 0,287 g. Masse émulsion : (meau +0,287) ; volume émulsion : Veau + 0,213 mL =(meau +0,287) /1,1942 avec meau = Veau. Par suite : Veau + 0,213 = (Veau +0,287) /1,1942 d'où Veau = 0,172 mL et volume de l'émulsion = 0,213 +0,172 =0,385 mL "0,385 mL de cette émulsion contenait 0,172 g d'eau et 0,287 g de gomme-gutte".
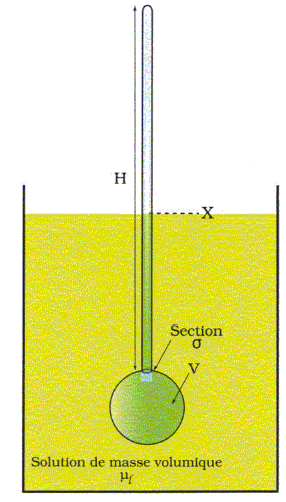
Le flotteur est en équilibre sous l'action de son poids ( valeur Mg ) et de la poussée d'Archimède ( valeur : (V+sX)µl g ). (V+sX)µl g = Mg ; (V+sX)µl = M ; V+sX = M /µl ; X = ( M /µl -V) / s . Rappeler la définition de la densité dl d'un liquide. Montrer qu'à l'équilibre, la lecture de la hauteur X donne accès à la densité. La densité d'un liquide par rapport à l'eau est égale à la masse d'un volume V du liquide divisée par la masse du même volume d'eau. La densité est encore égale à la masse volumique du liquide divisée par celle de l'eau. µl = M / (V+sX) ; dl = µl /µeau = M / (µeau (V+sX)). dl =M / (µeau V(1+sX/ V)). On pose e = sX/ V. dl =M / (µeau V (1+e)). Si e < 0,01 on suppose qu'il est possible d'effectuer l'approximation affine 1/(1+e) ~1-e. sX/ V < 0,01 ; s / V < 0,01 / X ; la plus grande valeur de X est 0,10 m : s / V < 0,1. On pose k = M / (µeau V) = constante. dl ~k ( 1-e ) =k - ksX/ V. La lecture de X peut donc donner la densité du liquide. On suppose qu'on peut graduer la hauteur H par demi-millimètre ( 0,5 mm ). Quelle précision sur la densité dl peut-on espérer sur cet appareil ? 200 graduations figurent sur la tige de hauteur H = 10 cm. 10/ 200 =0,05 pour chaque graduation. Proposer une manière de lester le flotteur. Utiliser un métal assez dense : par exemple mettre quelques billes de plomb dans le fond du flotteur. Un flotteur unique permet-il de mesurer toute densité avec une grande précision ? Justifier en donnant une condition pratique d'utilisation du flotteur. Dans le cas de liquides dont les densités s'étalent par exemple de 1 à 2 avec H = 10 cm et une graduation tous les 0,5 mm : 200 graduations correspondent à 1 ; une graduation correspond à 0,05. Graduation n°1 : d=1,00 ; graduation n°2 : d = 1,05 ; graduation n°3 : d = 1,10. La précision sur la densité est faible et il faudra utiliser différents types de flotteurs.
Méthode chimique : La masse de bromure de potassium (KBr) solide ajoutée est ms =28,135 g pour V0 = 100 mL de solution S finale. On donne M(KBr) =119 g/mol ; µKBr = 2,32 g cm-3. Exprimer puis calculer le volume Vs de KBr correspondant. Vs = ms / µKBr =28,135 / 2,32 =12,127 ~12,1 mL. Quelle réaction chimique est associée à cette mise en solution ? Ecrire l'équation chimique associée. Dissolution d'un solide ionique dans l'eau : destruction de l'édifice cristallin et hydratation des ions qui se dispersent en solution. KBr(s) = K+aq +Br-aq. Donner l'expression de la concentration molaire C de la solution S. faire l'application numérique. C = n(KBr) / V0 avec n(KBr) = ms / M(KBr) ; C =ms / ( M(KBr) V0 ). C = 28,135 / (119*0,100) =2,36 mol/L. On donne la courbe donnant la masse volumique d'une solution de bromure de potassium en fonction de la concentration à 20°C. Déterminer graphiquement la masse volumique µS de la solution S. 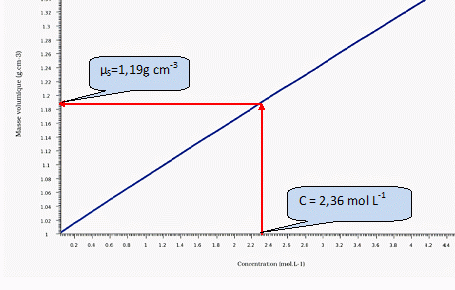
|
||||||
|
|