Dipole RL : concours Geipi 2011.

Afin de déterminer la résistance d’une bobine, on réalise un circuit série comprenant : • un générateur de tension continue E = 4,50 V et de résistance interne négligeable, • la bobine d’inductance L = 150 mH de résistance r inconnue, • une résistance étalonnée R de 10,0 Ω , • un interrupteur K. On branche aux bornes de la résistance R une carte d’acquisition informatisée permettant de visualiser les variations de la tension uR(t) après la fermeture de l’interrupteur K à t = 0. 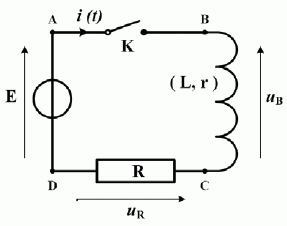Indiquer les points où doivent être branchés la masse M et la voie d’entrée Y de la carte d’acquisition. Pour visualiser la la tension uR(t) = uCD, le point D est relié à la masse et le point C est relié  à la voie d'entrée Y. Donner l'expression de la tension aux bornes de la bobine uB(t) en fonction de i(t). uB(t) = Ldi/dt + ri. Justifier qu’en introduisant la tension uR(t) aux bornes du résistor R, l’équation différentielle suivie par uR(t) s’écrit sous la forme : E = (1+r/R) uR +L/RduR/dt. Additivité des tensions : E = uR + uB ; de plus uR = Ri ; di/dt = 1/R duR/dt. E = uR + L/R duR/dt + r/R uR ; d'où : E = (1+r/R) uR +L/RduR/dt. (1) La solution de cette équation différentielle est de la forme : uR(t) = A + B exp (-t / τ). Donner les expressions de A et τ en fonction des éléments du circuit. duR/dt= -B/t exp (-t / τ). Repport dans (1) : E = (1+r/R)A + B (1+r/R) exp (-t / τ) - L/R B/t exp (-t / τ). On identifie : E = (1+r/R)A soit A = E / (1+r/R). B (1+r/R) exp (-t / τ) - L/R B/t exp (-t / τ)=0 ; (1+r/R) = L/(R t) soit t =L /  (R+r). Déterminer l’expression de B à partir de la condition initiale sur la valeur de uR à la fermeture de l’interrupteur K. La bobine introduit un retard à l'établissement du courant, i(0+) = 0 et uR(0+) = Ri(0+) =0. uR(0+) = A + B exp (0) = A+B = 0 soit B = -A = -E / (1+r/R). A partir de l’enregistrement de uR(t), déterminer, en indiquant précisément la méthode utilisée, la valeur numérique de τ. En déduire la valeur de la résistance r de la bobine. 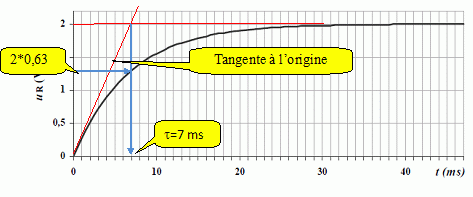R+r = L/t ; r = L/t -R = 0,150 / 7 10-3 -10,0 =11,4 ohms. Après un temps suffisamment long Δt, le régime permanent est atteint et on branche aux bornes B et C de la bobine un voltmètre numérique qui indique 2,494 V pour la tension uB. Calculer l’ordre de grandeur de la valeur minimale de Δt. Δt est de l'orre de 5 fois la consante de temps t : Δt ~ 5*7 = 35 ms. Donner l’expression de la tension uB en régime permanent. L'intensité, notée I, est constante en régime permanent : dI /dt = 0 et uB = rI. Additivité des tensions : E = uR + uB = RI + rI ; I = E/(R+r). uB =E r /(R+r). Donner l’expression et calculer la valeur de r à partir de la valeur de la tension lue sur le voltmètre. uB =E r /(R+r) ; uB(R+r) = E r ; R uB =r(E- uB) r =R uB / (E- uB) r = 10,0 *2,494 / (4,50-2,494) =12,4 ohms. Donner l’expression et calculer l’énergie WB emmagasinée dans la bobine. WB = ½LI2 avec I = E/(R+r).  WB = ½L E2/(R+r)2. WB = ½*0,150*4,52/(10,0+12,4)2=3,0 10-3 J.

menu