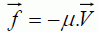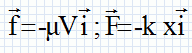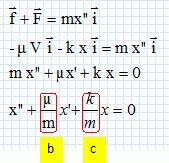Concours ESSA Lyon 2010 : réactions nucléaires, oscillateurs mécaniques.

QCM Ondes : Une onde sonore : a) Véhicule de la matière. ( faux ) b) Véhicule de l’information et de l’énergie ( vrai ) c) Est qualifiée d’onde mécanique transversale. ( faux ) Onde longitudinale. d) Se propage avec une célérité de 3.108 m/s dans le vide. ( faux ) ne se propage pas dans le vide. e) Voit sa fréquence inchangée dans les milieux dispersifs. ( faux ).  Une onde lumineuse se propage dans le vide avec une fréquence f0 et une longueur d’onde λ0. a) A un instant donné, les points de même état vibratoire sont distants de p.λ0 (p entier). ( vrai ) b) Dans un verre d’indice de réfraction n, la fréquence de l’onde est f0/n ( faux ) la fréquence reste constante quel que soit le milieu. c) Dans un verre d’indice de réfraction n, la fréquence de l’onde est n f0 ( faux ) d) Dans un verre d’indice de réfraction n, la longueur d’onde est λ0/n  ( vrai ). Applications thérapeutiques des rayonnements ionisants. L’iode-131 est un élément radioactif qui peut être volontairement administré à l’homme pour le traitement de maladies de la glande thyroïde ; est un émetteur β- de demi-vie T = 8 jours. Masse molaire (13153I = 131 g/mol; NA = 6 1023 mol-1 ; ln 2 ~0,7. 51Sb ( antimoine ) ; 52Te ( tellure ; 54Xe ( xénon ) ; 55Cs ( césium).   Donner la composition d'un noyau d'iode-131. Préciser ce qui le distingue de ses éventuels isotopes. 53 protons et 131-53 = 78 neutrons. Des isotopes ne diffèrent que par leur nombre de neutrons. Ecrire l'équation de désintégration de l’iode-131 en précisant les lois de conservation utilisées (on admettra que le noyau fils produit n'est pas obtenu dans un état excité). 13153I --> AZX  +0-1e Conservation de la charge : 53 = Z -1 d'où Z = 54 ( élément Xe ). Conservation du nombre de nucléons : 131 =A+0. 13153I --> 13154Xe  +0-1e. D'où provient la particule émise par 131I lors de sa désintégration ? Quelle différence fondamentale existe-t-il entre cette particule et celle mise en jeu lors des réactions chimiques d'oxydo-réduction ? Un neutron du noyau se transforme en proton : 10n -->11p +0-1e. Cet électron émis lors d'une réaction nucléaire possède une énergie très supérieure à celle d'un électron mis en jeu au cours d'une réaction d'oxydo-réduction ( réaction chimique ). Soit un échantillon contenant une masse m0 gramme d’iode-131, d’activité initiale A0 Bq. Etablir l’expression de la masse m0 en fonction de A0, T et NA. Nombre de noyaux d'iode 131 : N0 = m0/M NA. Loi de décroissance radioactive : N(t) = N0 exp (-lt) avec l = ln2/T. A(t) = -dN(t) / dt = N0 l exp (-lt)= A0 exp (-lt) d'où : A0 = l N0 = ln2 / T N0 = ln2 / T m0 / M NA. m0 =A0 T M / ( NA ln2). Quelle est la valeur de m0 si A0 = 70 MBq ? m0 =70 106 *8*24*3600* 0,131 / ( 6 1023 *0,7). m0 = 108 *8*24*3600* 0,131 / ( 6 1023 ) =108 *8*24*600* 0,131 /  1023 =8*24*6* 0,131 /  10-13 =1,5 10-11 kg =1,5 10-8 g = 15 ng. On administre 80 MBq à un patient et on suppose que tous les noyaux d’iode-131 injectés se fixent sur la thyroïde. Quelle sera l'activité résiduelle (en MBq) 32 jours après cette injection ? 32 jours = 4*8 = 4 T. A(t=32) = A0 / 24 =80/16 = 5,0 MBq. 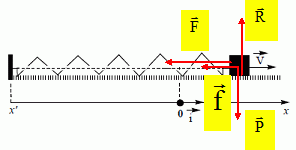Modélisation biomécanique du corps humain pour les mouvements de vibration. Les troubles musculo-squelettiques présentés par certains sujets soumis à des vibrations durant leur activité professionnelle s’expliquent par une mise en résonnance du système (thorax-bassin). En biomécanique, ce système est modélisé par un mobile de masse m fixé à un ressort de masse négligeable et de raideur k. Le mobile oscille sur un plan horizontal et au repos, son centre d’inertie coïncide avec l’origine O d’un axe x’Ox orienté de gauche à droite (voir schéma ci-dessous). 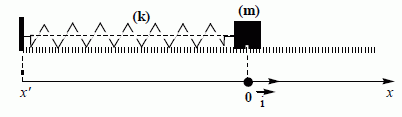Modélisation idéale du système thorax-bassin. Donner les propriétés d'une solution tampon. Dans ce modèle, on néglige les forces de frottement ; le mobile oscille alors périodiquement autour de sa position d’équilibre O avec une fréquence propre de 5 Hz. Si le mobile est en sa position d’équilibre, exprimer, en fonction de T0, la durée nécessaire pour observer un nouveau passage par cette position d’équilibre. Justifier. Toutes les demi-périodes, ½T0, le mobile passe par la position d'équilibre, en sens contraire du passage précédent. x(t) = Xm sin( 2pt / T0 ) = 0 soit  : sin( 2pt / T0) =0 ou 2p t / T0 =  2k p ; t = kT0. et sin( 2pt / T0) =0 ou 2p t / T0 = p- 2k p ; t = |k-0,5|T0. ( k entier ). La solution de l’équation différentielle du mouvement du mobile est du type : x(t) = Xm cos( 2pt / T0 + J0). Exprimer T0 en fonction de k et de m. T0 = 2 p (m/k)½. Définir les constantes Xm et ϕ0 et préciser leur unité dans le système international. Xm : amplitude positive en mètre ; J0 : phase à l'origine en radian. A t = 0, on lâche le mobile sans vitesse d’une position x0 = - 5 cm ; la raideur est 20 000 N.m-1 . Si l’énergie potentielle de pesanteur est nulle sur le plan, que vaut (en J) l’énergie mécanique du mobile : A l’instant initial ? Justifier. L'énergie cinétique initiale est nulle ( vitesse initiale nulle ). L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. L'énergie potentielle initiale  est égale à l'énergie mécanique et vaut ½lx02 =0,5 *20 000 *(5 10-2)2 =0,5*2*25 =25 J. A l’instant où le mobile repasse pour la première fois par sa position d’équilibre ? Justifier. En absence de frottement, l'énergie mécanique se conserve. Au passage à la position d'équilibre, x=0, l'énergie potentielle est nulle. L'énergie cinétique est maximale, égale à l'énergie mécanique. Modélisation amortie du système thorax-bassin. Dans ce modèle, les forces de frottement subies par le mobile sont équivalentes à une force unique proportionnelle à sa vitesse où μ est une constante positive. On se place à un instant où le mobile est à droite du point O (entre sa position d’équilibre et sa position d’écartement maximum) avec un déplacement de gauche à droite (voir schéma ci-dessous). Pour cet instant, représenter et nommer les forces extérieures exercées sur le mobile. Le mobile est soumis à son poids P, verticale, vers le bas, valeur mg, à l'action du plan, opposée au poids, à la force de frottement et à une force de rappel F exercée par le ressort. Pour cet instant, donner l’expression des forces de rappel F et de frottement f en fonction de x, V, k, μ et du vecteur unitaire i. Préciser, en le justifiant, les signes de x et V. L'abscisse x est positive et le vecteur vitesse a le sens du vecteur unitaire. V est donc positif. L’équation différentielle du mouvement du mobile est de type : x" +b x' + c x 0 où b et c sont des constantes. Etablir l’expression des constantes b et c en fonction de μ, m et k Ecrire la seconde loi de Newton sur l'axe x'Ox. Application pratique de la modélisation du système (thorax-bassin) : On considère une voiture transmettant intégralement les vibrations de la route à ses passagers. Elle roule à la vitesse V0 = 72 km/h sur une route bosselée où les bosses sont distantes de L. On s’intéresse aux effets de cette route sur le système (thorax-bassin) modélisé en (II) et de fréquence propre 5 Hz. Dans ces conditions d’oscillations : Quel est le qualificatif utilisé pour nommer les oscillations du système (thorax-bassin) ? Ce sont des oscillations forcées. Quel est le qualificatif utilisé pour la route bosselée ? Pour le système (thorax-bassin) ? La route bosselée joue le rôle d'excitateur ; le système bassin-thorax joue le rôle de résonateur. Exprimer la fréquence de répétition (FRep) des bosses rencontrées en fonction de L et de V0. V0 / 3,6 = 72 / 3,6 = 20 m/s ; durée pour parcourir la distance L : T = L / (V0 / 3,6 ) = 3,6 L / V0. FRep = 1/T = V0/ (3,6 L) On s’intéresse à la mise en résonance du système (thorax-bassin) par la route bosselée. Définir le phénomène de résonance et la condition pour laquelle il est observé. Pour une fréquence FRep ~ f0 ( fréquence propre du système thorax-bassin) , l'amplitude des oscillations passe par une valeur maximale. Quelle doit être, en mètre, la distance L séparant deux bosses pour observer la résonance ? L = V0/ (3,6 f0) =72 / (3,6*5) =20 / 5 = 4 m.

menu