|
QCM
physique :
concours ergothérapeute Berck 2010 |
|||||||||||
|
|||||||||||
|
On donne le graphe représentant l'évolution de la vitesse au cours du temps. 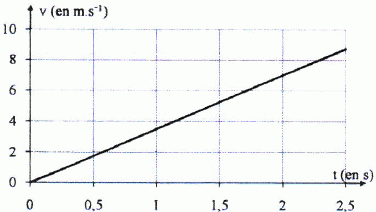 On donne g = 10 m s-2 et sin 30 = 0,5. Calculer la valeur de f (N). (0,20 ; 0,30 ; 0,40 ; 0,50 ; 0,60 ; aucune réponse exacte ). Le coefficient directeur de la droite représente l'accélération : Dv/Dt = 8 / 2,3 ~3,5 m s-2. Le solide est soumis à son poids ( verticale vers le bas, valeur mg ) , à l'action du plan ( perpendiculaire au plan ) et à la force de frottement. Ecrire la seconde loi de Nexton sur un axe parallèle au plan, dirigé vers le bas. 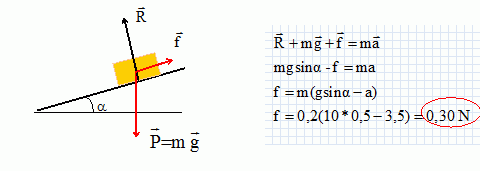
Déterminer la valeur de la vitesse du satellite ( km/h ) dans le référentiel géocentrique. Un oscillateur est constitué par un solide de masse m = 200 g
accroché à l'extrémité d'un ressort à spires non jointives, de masse
négligeable et de constante de raideur k. Le solide S oscille sans
frottement suivant un plan horizontal. On repère la position, à
l'instant t, du centre d'inertie G de S par l'abscisse x, sur un axe
horizontal dont l'origine correspond à la position du centre d'inertie
au repos. l'équation du mouvement de G, exprimée en unités du système
international, s'écrit : x(t) = 4,0 10-2 cos( 2pt / 1,6). On donne p2 ~ 10. Déterminer la valeur de la force ( mN) exercée par le ressort sur le solide à l'élongation maximale.
Un courant d'intensité I0 = 4,0 A circule dans un solénoïde de longueur L = 50 cm et comportant un nombre N inconnu de spires. On mesure à l'aide d'un teslamètre la valeur du champ magnétique au centre du solénoïde et on trouve B0 = 5,0 mT. On fait ensuite circuler un courant I1 = 7,2 A et on mesure la nouvelle valeur B1 du champ magnétique au centre du solénoïde. On donne µ0 = 4 p 10-7 SI. Calculer la valeur de B1 ( mT). 2,7 ; 5,0 ; 6,2 ; 7,2 ; 9,0 ; aucune réponse exacte. B0 = µ0 N I0/L = k I0 ; B1 = µ0 N I1/L = k I1 avec k une constante. B1 = B0 I1 /I0 = 5,0 *7,2 / 4 = 5,0 *1,8 = 9,0 mT. On considère la réaction de fusion suivante : 21H + 31H --> 42He + 10n. On donne : m(21H) = 2,014 u ; m(31H) = 3,016 u ; m(42He) = 4,002 u ; m(10n) = 1,008 u. 1 u ~ 1,6 10-27 kg ; 1 eV = 1,6 10-19 J ; c = 3,0 108 m/s. Calculer la valeur de l'énergie ( MeV) libérée par cette réaction de fusion. Dm =m(10n) + m(42He) -m(31H) -m(21H) = 1,008 + 4,002 -2,014 -3,016 = 5,01 -5,03 = -0,02 u . 0,02 *1,6 10-27 = 3,2 10-29 kg. Energie libérée E = |Dm |c2 = 3,2 10-29 *9 1016 = 3,2 * 9 10-13 J. 3,2 * 9 10-13 / 1,6 10-13 =2*9 = 18 MeV.
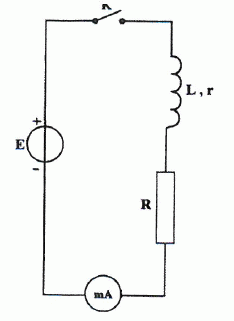
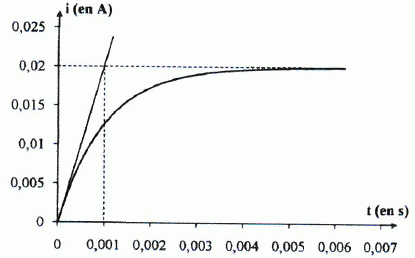
- L'inductance de la bobine vaut L = 300 mH. Vrai. Intensité en régime permanent I = E / (R+r)= 0,02 A d'où R+r = E/I = 6,0 / 0,02 = 300 ohms Constante de temps t = L/(R+r) = 0,001 s. L = t(R+r) =0,001 *300 = 300 mH. - La résistance r vaut 80 ohms. Vrai. - La constante du circuit vaut t = 1,0 10-2 s. Faux. - La tension aux bornes de la bobine en régime permanent est de 1,6 V. Vrai. rI = 80 *0,02 = 1,6 V. - L'énergie stockée dans la bobine est de 60 µJ en régime permanent. Vrai. ½L I2 = 0,5*0,3 *0,022 = 6,0 10-5 J = 60 µJ.
|
|||||||||||
| |
|||||||||||
|
|