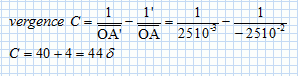Comment peut-on adapter sa vision ? Oeil, loupe, microscope : concours interne CAPLP maths sciences 2011

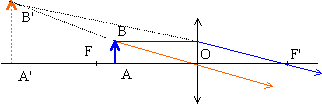
Comment peut-on adapter sa vision ? Généralités. En optique qu'appelle t-on lentille ? Une lentille est un dispositif homogène, isotrope (  invariance des propriétés du milieu en fonction  de la direction de propagation de la lumière ), transparent, bien souvent réalisé en verre.L’une des faces n’est pas plane. Une lentille fait converger ou diverger la lumière. Dans la suite de l'exercice, nous nous limiterons aux lentilles minces. Comment définit-on une lentille mince ? Une lentille mince est une lentille dont l'épaisseur est faible devant les rayons de courbure de ses faces. La figure suivante représente la coupe d'une lentille convergente biconvexe. Modéliser cette lentille par un schéma en précisant le sens de propagation de la lumière. 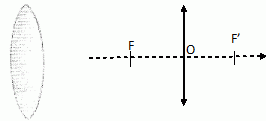Sur une lentille on lit l'information suivante : - 2 d. Que signifie cette information ? Comment expliquer le signe négatif du nombre ? La vergence de cette lentille est égale à - 2 dioptries. La lentille est divergente. Un système est composé de deux lentilles minces accolées, de vergences respectives C1 = 5 d et C2 = -3 d. Déterminer la vergence de l'association ainsi que la distance focale image de la lentille équivalente. C = C1+C2 = 5-3 = 2 dioptries ; distance focale image f ' = 1/C = 1/2 = 0,50 m. Pour obtenir des images de qualité avec des lentilles, on doit se placer dans les conditions de Gauss. Quelles sont ces conditions ? L'objet doit être de petites dimensions et placé au voisinage de l'axe optique principal du système optique. On élimine ainsi les rayons lumineux trop inclinés sur l'axe optique. L'oeil modélisé. La partie transparente de l'oeil ( humeur aqueuse, cristallin, cornée ...) peut être modélisée par une lentille mince convergente. Les images des objets observés se forment sur la rétine ( qui joue le rôle d'un écran que l'on supposera plan dans la zone où se forme l'image ). La distance rétine-lentille est égale à 25 mm. Pour observer la tache du patient, le médecin regarde à l'oeil nu. Pour modéliser cette situation, on a placé un objet à 25 cm devant l'oeil. Reproduire le schéma, construire l'image de l'objet AB et préciser la position du foyer image en justifiant. 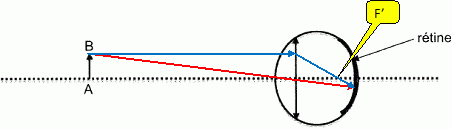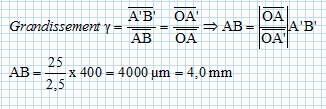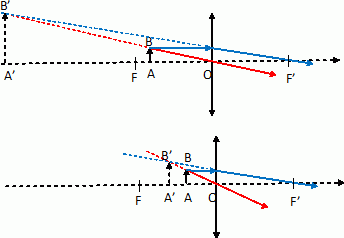La taille de l'image sur la rétine est de 400 µm. Calculer la taille de l'objet AB. Calculer la vergence de l'oeil dans cette situation.   La loupe : La vision à l'oeil nu n'étant pas assez précise, le médecin décide d'utiliser une loupe pour mieux observer la tache du patient. On utilise une même loupe, à des distances différentes, d'un même objet fixe. Justifier à l'aide de schémas légendés, les réponses aux questions suivantes : Quel est le rôle d'une loupe ? L'image est virtuelle, plus grande que l'objet observé et de même sens que l'objet. Où placer l'objet pour utiliser  la loupe au maximum de ses possibilités ? L'objet doit être compris entre O et le foyer objet F et le plus près possible de F. Proposer un protocole expérimental à destination des élèves de baccalauréat permettant de réaliser des mesures et de les exploiter à l'aide d'un tableur pour établir les relations de conjugaison et de grandissement d'une lentille et pour déterminer graphiquement la vergence de cette lentille. On réalise l'expérience suivante sur le banc d'optique : On dispose une plaque métallique (M), dans laquelle est découpée une lettre, devant une lampe allumée. A une distance  D = 2,0 m, de la plaque (M) on fixe un écran (E) parallèlement à la plaque. On interpose entre la plaque et l'écran une lentille convergente (L). On déplace celle-ci à partir de la plaque (M) afin d'obtenir sur l'écran une image nette de la lettre découpée. On mesure la distance entre la plaque (M) et la lentille (L), la distance lentille-écran, la hauteur de l'objet et la grandeur de l'image. On procède de même pour différentes positions de la lentille et de l'écran. On note à chaque fois les distances lentille-objet, lentille-image ( écran) et la grandeur de l'image. On note : p = - distance lentille-objet ( mètre ) ; p' = distance lentille-image ( mètre) ; AB : hauteur de l'objet ( mètre) ; A'B' = - grandeur de l'image ( mètre) Regrouper les résultats dans un tableau : p p' AB A'B' A'B' / AB p' / p 1 / p 1 / p' Construire le graphe d'équation : 1 / p' en fonction de 1/p. On obtient une droite ; l'ordonnée à l'origine donne la vergence de la lentille. Le microscope. Pour affirmer son diagnostic, le médecin prélève un échantillon de la tache afin de l'observer au microscope. Un microscope est un instrument qui comprend deux systèmes optiques convergents, que l'on suppose réduits chacun à une lentille mince : - l'objectif L1 de centre optique O1 devant lequel est situé l'objet - l'oculaire L2 de centre optique O2 placé devant l'oeil de l'observateur. Les deux systèmes ont le même axe optique. Faire un schéma expliquant le principe du microscope. On précisera en particulier le rôle de l'oculaire. 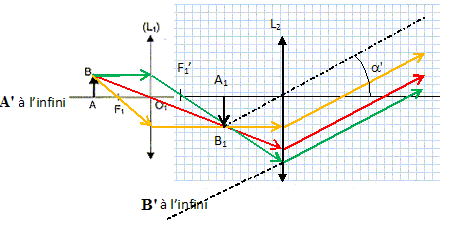L'oculaire fonctionne en loupe. On donne pour un microscope : O1O2 = 12 cm ; distance focale de L1 : f1= 2 mm , distance focale de L2 : f2= 2 cm ; hauteur de l'objet AB = 1 µm ; distance objet-L1 =2,04 mm. Calculer la position et la taille de l'image intermédiaire A1B1. 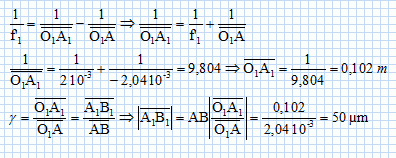Déterminer le diamètre apparent a' de l'image de A1B1 par L2. tan a' = A1B1 /O2A1. O2A1 = O1O2-O1A1 = 0,12 -0,102 =1,8 10-2 m tan a' =50 10-6 / 1,8 10-2 =2,78 10-3. a' =2,8 10-3 rad. Déterminer le diamètre apparent a de l'objet observé à l'oeil nu, à la distance de 25 cm. tan a = AB /0,25 = 10-6 / 0,25 = 4,0 10-6 ; a =4,0 10-6 rad. Calculer le grossissement G = a'/a du microscope. G = 2,8 10-3 / 4,0 10-6 = 700. La résolution du microscope optique est sa capacité à séparer des objets très proches. On admet que la limite de résolution d représentant la plus petite distance en dessous de laquelle deux objets voisins ne seront plus distingués est donnée par la relation :d = l / ( 2n sin a) où l est la longueur d'onde d'éclairage, n l'indice de réfraction du milieu et n sin a l'ouverture numérique. Dans l'air, calculer d pour une longueur d'onde de 650 nm et une ouverture numérique de 0,25. d = 650 10-9/(2*0,25) = 1,3 10-6 m = 1,3 µm. En restant dans le domaine du spectre visible, quelle est la longueur d'onde qui permettra d'avoir la résolution la plus grande ? Le spectre visible s'étend de 400 nm à 800 nm : donc 800 nm. La luminothérapie. L'examen au microscope permet au médecin de proposer un traitement médical appelé luminothérapie. Ce traitement consiste en une exposition quotidienne face à une lampe de luminothérapie médicale recréant une lumière solaire artificielle dépourvue de rayons ultraviolet et infrarouge. Sur un axe gradué en nm, positionner les rayonnements ultrat violet et infrarouge ainsi que le spectre visible par l'homme. Un patient achète une lampe de luminothérapie médicale d'intensité 10 000 lux. Cette lampe doit être utilisée à une distance minimum de 60 cm. Le traitement du patient consiste en une exposition de 5 000 lux et celui-ci annonce qu'il peut utiliser la lampe achetée mais en doublant la distance ce qui divisera par deux l'intensité. Proposer une expérience permettant de valider ou d'invalider le raisonnement fait par le patient. L'éclairement, à la verticale de la source, est inversement proportionnel au carré de la distance. Placer, à la verticale de la source, un luxmètre à une distance de 50 cm et noter l'éclairement. Refaire la même expérience à la distance de 1 m à la verticale de la source.

menu