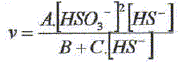Cinétique d'une réaction d'oxydation de HS- par HSO3- : concours Caplp maths sciences 2011

Aurélie 19/12/10

Cinétique d'une réaction d'oxydation de HS^- par HSO₃^- : concours Caplp maths sciences 2011

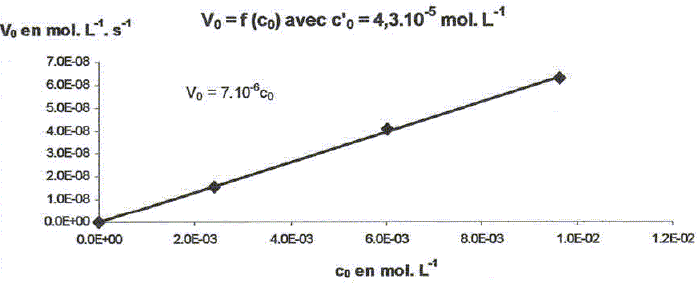
On étudie la cinétique de la réaction suivante :
2HS^-aq + 4HSO₃^-aq = 3S₂O₃^2-aq + 3H₂O(l).
On détermine la vitesse de formation initiale v₀ à 20°C des ions thiosulfate pour différentes concentrations molaires initiales de HS^-aq notée c₀ et HSO₃^-aq notée c'₀. On donne les résultats expérimentaux.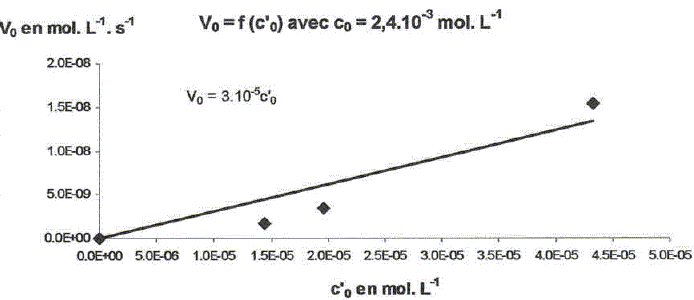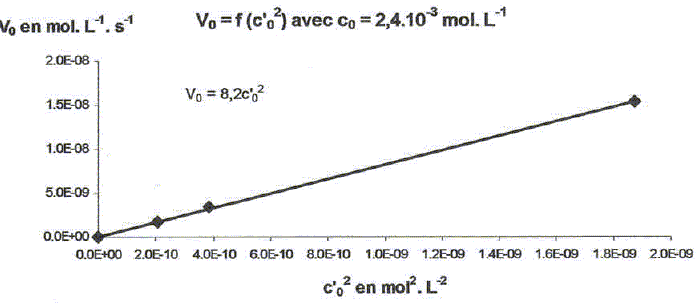

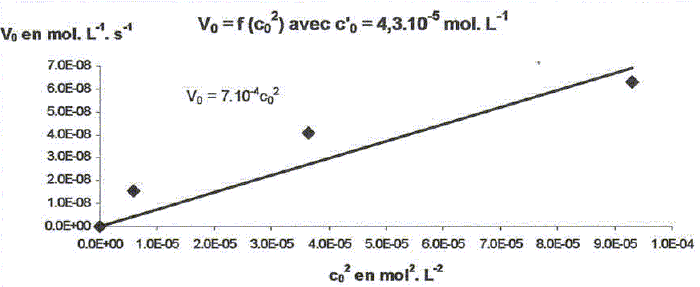Définir la vitesse volumique v de formation des ions thiosulfate S₂O₃^2-aq.
Vitesse de la réaction : v = 1/V dx/dt avec V : volume de la solution et x : avancement (mol).
état avancement (mol) 2HS^-aq + 4HSO₃^-aq = 3S₂O₃^2-aq + 3H₂O(l).
initial 0 c₀V c'₀V 0 solvant
en cours x c₀V-2x c'₀V-4x 3x solvant
[S₂O₃^2-aq]=3x/ V ; vitesse de formation des ions thiosulfate d[S₂O₃^2-aq] /dt = 3/V dx/dt = 3 v.
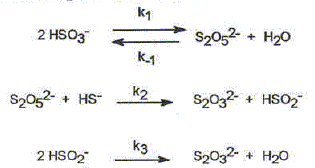
Décrire une méthode permettant la détermination de la vitesse initiale v₀ de formation des ions thiosulfate.
Déterminer l'avancement x de la réaction pour différentes valeurs du temps et tracer la courbe x = f(t).
Le coefficient directeur de la tangente à l'origine de cette courbe est proportionnel à la vitesse initiale de la réaction au facteur V près.
On note a l'ordre partiel par rapport à HS^-aq, ß l'ordre partiel par rapport à HSO₃^-aq et k la constante de vitesse.
Montrer que v₀ = kc₀^a c'₀^ß.
[ d[S₂O₃^2-aq] /dt]₀ = 3v₀ = 3kc₀^a c'₀^ß.
Déterminer a et ß ainsi que l'ordre global de la réaction.
c₀ étant constante, c'₀ varie : [ d[S₂O₃^2-aq] /dt]₀ =K'c'₀^ß . avec K' =3kc₀^a = constante.
Le premier graphe d'équation v₀ = f(c'₀) n'est pas une droite : a est différent de 1.
Le second graphe d'équation v₀ = f(c'²₀) est une droite : a est égal à 2 et K' = 8,2 avec c₀ = 2,4 10^-3 mol/L.
c_'0 étant constante, c₀ varie : [ d[S₂O₃^2-aq] /dt]₀ =K''c₀^a . avec K'' =3kc'₀^ß = constante.
Le 3è graphe d'équation v₀ = f(c₀) est une droite : ß est égal à 1 et K'' = 7 10^-6 avec c'₀ = 4,3 10^-5 mol/L.
D'où : 8,2 = 3k c₀ = 3* 2,4 10^-3 k ; k = 1,14 10³ ~1,1 10³ L²mol^-2 s^-1.
et 3kc'₀² = 7 10^-6 = 3k (4,3 10^-5)² ; k = 1,26 10³ ~1,2 10³ L²mol^-2 s^-1.
On retient k ~ 1 x10³ L²mol^-2 s^-1 et a = 2 et ß = 1. L'ordre global est égal à 3.

La constante de vitesse k a été déterminée à différentes températures :
T(K) 273 283 293 303 313
k 303 613 1 x 10³ 2033 4667
ln k 5,71 6,42 6,9 7,62 8,45
1 / T 3,66 10^-3 3,53 10^-3 3,41 10^-3 3,30 10^-3 3,19 10^-3

Rappeler la loi d'Arrhénius puis déterminer l'énergie d'activation de la réaction.
k = pZ exp(-E_a/(RT)) avec p : facteur stérique ; Z : facteur de fréquence et E_a : énergie d'activation positive.
ln k = ln(pZ) -E_a/(RT). On trace la droite d'équation ln k = f(1/T ) ; son coefficient directeur vaut -E_a/R avec R = 8,31 J mol^-1 K^-1.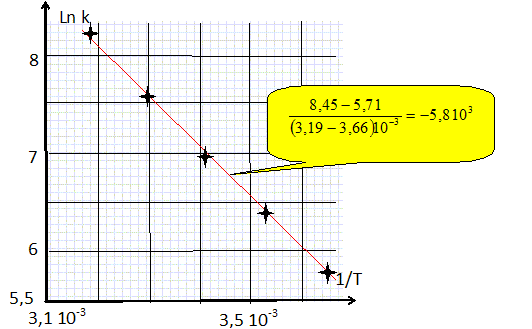

E_a= 5,8 10³ *8,31 ~ 48 kJ /mol.

On propose le mécanisme suivant pour cette réaction :

En utilisant l'approximation des états quasi-stationnaires pour les espèces S₂O₅^2- et HSO₂^-, montrer que la vitesse de formation du thosulfate peut s'écrire :

d[S₂O₅²^-] /dt = 0 = k₁[HSO₃^-]²-k_-1[S₂O₅²^-]-k₂[S₂O₅²^-][HS^-] (1)
d[HSO₂^-] /dt =0 = k₂[S₂O₅²^-][HS^-]-k₃[HSO₂^-]². (2)
d[S₂O₃^2-]/dt = k₂[S₂O₅²^-][HS^-] +k₃[HSO₂^-]². (3)
(1) donne : [S₂O₅²^-] =k₁[HSO₃^-]² / (k_-1+k₂[HS^-]) (4)
(2) donne : k₃[HSO₂^-]² = k₂[S₂O₅²^-][HS^-]
tenir compte de (4) : k₃[HSO₂^-]² = k₂k₁[HSO₃^-]² [HS^-] / (k_-1+k₂[HS^-]).
Repport dans (3) :
d[S₂O₃^2-]/dt = k₂k₁[HSO₃^-]² [HS^-]/ (k_-1+k₂[HS^-]) + k₂k₁[HSO₃^-]² [HS^-] / (k_-1+k₂[HS^-])
d[S₂O₃^2-]/dt =k₂k₁[HSO₃^-]² [HS^-] / (k_-1+k₂[HS^-].
On identifie A à k₂k₁ , B à k_-1 et C à k₂.
Quelle hypothèse doit-on faire pour retrouver l'expression de la vitesse déterminée expérimentalement ? k_-1>>k₂[HS^-] ; le premier équilibre est rapide ; la seconde étapeest lente.

menu