Questions de culture générale. Répondre brièvement aux questions :
Parmi les moteurs électriques alimentés en courant alternatif, on distingue les machines synchrones et asynchrones
Avec
quelle grandeur la fréquence de rotation doit-elle être comparée pour
définir si le fonctionnement est synchrone ou asynchrone ?
La vitesse de rotation des machines synchrones est toujours proportionnelle à la fréquence des courants qui les
traversent. ce n'est pas forcément le cas pour les machines asynchrones.
Un moteur électrique peut-il être utilisé comme générateur d'énergie électrique ?
Une machine synchrone est souvent utilisée comme alternateur.
Les carcasses des moteurs électriques sont réalisées en alliage à base de fer.
Pourquoi n'utilise t-on pas l'aluminium ?
L'aluminium ne possède aucune propriété ferromagnétique. Le stator du moteur doit crée le champ magnétique.
Les matériaux ferromagnétiques.
Les aimants les plus puissants actuellement contiennent des "terres rares".
A quoi correspond cette dénomination ?
Famille des lanthanides.
En
dehors du fer, deux autres métaux de transition ayant des propriétés
ferromagnétiques sont souvent utilisés en électromécanique.
Lesquels ?
Cobalt et nickel.
Définir le sens des termes suivants utilisés pour caractériser des aimants.
Température de Curie : température pour laquelle le matériau perd son aimantation, de façon réversible.
Champ permanent : un aimant permanent est constitué de matériaux ferromagnétique à large
cycle d’hystérésis il conserve son magnétisme
entièrement ou en partie après une magnétisation précédente.
Excitation de désaimantation : Pour annuler ou inverser l'aimantation, il est nécessaire
de fournir une excitation magnétique.
Les conducteurs électriques.
Classer les trois métaux suivants par ordre de résistivité croissante à température ambiante : aluminium, argent et cuivre.
Aluminium, cuivre, argent.
Donner la place de l'or dans ce classement.
Aluminium, or, cuivre, argent.
Quelle est l'unité de la résistivité dans le système SI ? ohm mètre W m.
Equations électromécaniques d'une machine à courant continu.
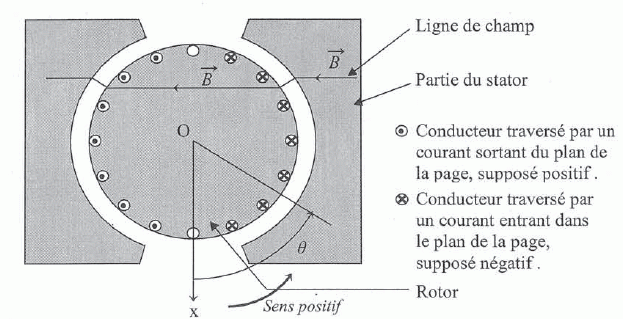
Le schéma ci-dessous représente le rotor et une partie du stator d'une machine à courant continu.
Le rotor comporte NE encoches ; chaque encoche contient NC
conducteurs. La distance entre les conducteurs et le centre O du rotor
est notée r. La longueur des conducteurs placés dans le rotor est notée
l. Le champ magnétique
dans l'entrefer ainsi que dans les encoches contenant les conducteurs
est supposé parfaitement radial. On supposera que le champ magnétique
interagit avec le courant circulant dans les conducteurs.
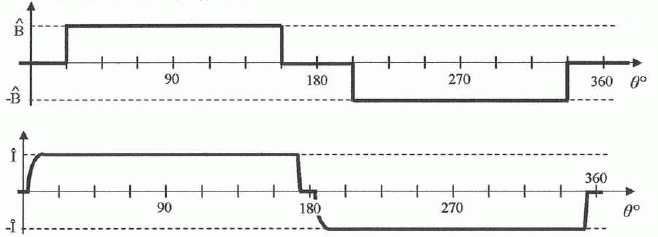
L'allure de la répartition du champ magnétique dans l'entrefer en fonction de l'angle q
repéré à partir de l'axe Ox est donné. Il est considéré comme positif
quand le champ va du stator vers le rotor et négatif dans le cas
contraire.
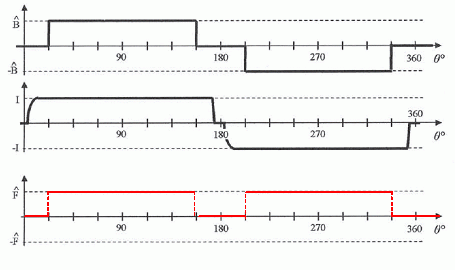
L'intensité du courant traversant les conducteurs d'une encoche en fonction de la position q de l'encoche est donnée.
Représenter l'allure du module FT de la force tangentielle agissant sur l'ensemble des NC conducteur d'une encoche en fonction de sa position angulaire q.
Elle sera considérée comme positive quand elle aura pour effet d'entraîner le rotor dans le sens positif.
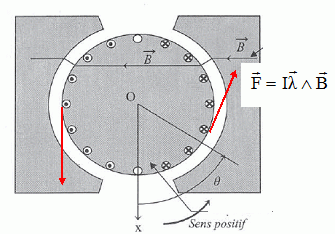
Pour q =
90 °, donner l'expression de la valeur du module de la force
tangentielle agissant sur l'un des conducteurs logés dans une encoche.
FT90 = I l B. Soit pour NC conducteurs : FT90 =NC I l B.
Donner en fonction de FT90, l'expression de la valeur moyenne calculée sur un tour du module de la force qui agit sur l'ensemble des conducteurs contenus dans une encoche du rotor.
FT90 = 0 entre 0 et 22,5°, 157,5 et 202,5° et entre 337,5 et 360° soit pendant 90°. Dans les autres intervalles, elle vaut NC I l B pendant 270°.
Par suite la valeur moyenne est : 0,75 NC I l B = 0,75 FT90.
En déduire
l'expression de T, le moment du couple qui agit sur le rotor ; mettre
ce dernier sous la forme KI et donner l'expression de K en fonction de
B, l, r, NC et NE.
T = NE r 0,75 FT90 = NE r 0,75 NC I l B.
On pose K = NE r 0,75 NC l B.
Calculer K.
B = 0,34 T ; l = 12 cm ; r = 4,2 cm ; NE = 24 ; NC = 40.
K = 24*40*0,042*0,75*0,12 *0,34 =1,23 ~1,2 N m A-1.
Ce couple moteur entraîne le moteur dans le sens positif.
Donner l'expression de la vitesse tangentielle, notée vT, d'une encoche en fonction de r et de W, la fréquence de rotation en rad/s.
vT = W r.
Donner l'expression de la fem e induite dans un conducteur contenu dans une encoche en fonction de B, l, r et W. Pour q = 90°.
e = B l vT = B l W r.
Donner les expressions des produits eNCI et FT90 vT en fonction de B, l, r, W et I.
eNC I = B l W r NC I ; FT90 vT = NC I l B W r.
Ces deux produits correspondent à une puissance et s'expriment en watt.
Etude du fonctionnement en moteur.
Le moteur étudié est utilisé pour motoriser un tour qui permet de travailler des pièces en bois.
C'est un moteur à aimant permanent parfaitement compensé. Il fonctionne
donc à flux constant. Dans ces conditions, la force électromotrice E
peut s'exprimer sous la forme E = kn, relation dans laquelle n désigne
la vitesse de rotation exprimée en tr min-1 ; on donne k = 0,13 V min tr-1. La résistance de l'induit, mesurée à la température de fonctionnement, est R = 2,7 W.
Dans la suite du problème, on considèrer que la machine peut être
modélisée par un circuit électrique constitué par une fem E en série
avec la résistance R.
Détermination de quelques caractéristiques de la machine.
Le moteur, alimenté sous tension nominale Un = 210 V, développe un couple égal au couple nominal et absorbe un courant d'intensité In = 5,6 A. On note W la vitesse angulaire mesurée en rad s-1.
Montrer que E = KW et calculer K.
n tr min-1 = 2 p n / 60 rad s-1 ; W =2 p n / 60 rad s-1 d'où n = 60 W / (2p).
E = k n =k 60 W / (2p) = K W avec K =60k / (2p) = 60*0,13 / 6,28 =1,242 ~ 1,2 V s rad-1.
Si on néglige les pertes autres que par effet Joule, on peut admettre que la puissance électromagnétique Pem = EI est égale à la puissance mécanique utile T W où T est le moment du couple utile.
Montrer que T peut se mettre sous la forme T = KI.
Pem = E I = T W ; de plus E = K W d'où : T = K I.
Calculer
la valeur du couple nominal Tn.
Tn = K In = 1,242 *5,6 = 6,955 ~7,0 N m.
Montrer que la vitesse de rotation nominale est nn = 1500 tr /min.
Un = E + RIn soit E = 210-2,7*5,6 =194,88 V.
E I = T W d'où W = E I / T = 194,88 *5,6 / 6,955 = 156,91 rad/s
nn=156,91 / 6,28 *60 =1499,16 ~1,5 103 tr min-1.
Mise en vitesse de la machine.
Dans
cette partie, on supposera que le moment du couple moteur de la machine
peut se mettre sous la forme T = KI avec K = 1,2 N m A-1.
Le rotor et la pièce de bois entraînée présentent un moment d'inertie J par rapport à l'axe de rotation. J = 4,5 10-3 kg m2.
Le moteur est alimenté par une alimentation électrique qui permet le contrôle des tensions et des courants délivrées.
Alimentation à courant constant.
Le générateur impose un courant constant ( et donc un couple constant ) égal au courant nominal In = 5,6 A jusqu'à ce que la tension soit égale à la tension nominale Un.
En première approximation, il est possible de négliger les pertes mécaniques.
Donner l'expression de l'équation différentielle qui régit les variations de W au cours du temps en fonction de J et Tn.
Appliquons la relation fondamentale de la dynamique au rotor du moteur
; le seul couple appliqué est le couple moteur ( le moteur est à
vide ) : Tn = J dW / dt.
Or le couple Tn est lié au courant par la relation : Tn = KI = constante.
Déterminer la durée nécessaire au moteur pour, partant de l'arrêt, atteindre la vitesse nominale nn = 1500 tr/min.
W = Tn / J t + constante ; à t = 0, W=0, la constante d'intégration est donc nulle.
W = Tn / J t ; t = W J / Tn =156,91 *4,5 10-3 / (1,2*5,6) =0,10506 ~0,11 s.
Alimentation à puissance constante.
Le générateur délivre un courant et une tension de telle manière que la
puissance électrique fournie soit constante et égale à la puissance
nominale d'alimentation du moteur notée Pn et supposée égale à 1100 W.
Montrer qu'à l'instant du démarrage au cours duquel le moteur ne tourne pas encore, le courant est proche de 20 A.
U = E + R I avec E = 0 à l'instant du démarrage ( rotor à l'arrêt ).
Pn = U I = RI2 ; I = (P / R)½ =(1100 / 2,7)½= 20 A.
Expliquer qualitativement pourquoi le démarrage est plus rapide que dans le cas où l'alimentation fonctionne à courant constant.
L'intensité du courant est bien plus grande qu'à courant constant d'intensité In. Or le couple moteur est proportionnel à l'intensité.
Alimentation à tension constante.
Le générateur délivre une tension constante et égale à la tension Un = 210 V.
Avec ce procédé, la mise en route est très brutale. Montrer que l'intensité du courant de démarrage est supérieure à 75 A.
E + R I avec E = 0 à l'instant du démarrage ( rotor à l'arrêt ).
Un =RI ; I =Un /R = 210 /2,7 ~78 A.
Déterminer l'expression du moment du couple moteur en fonction de la vitesse du rotor.
Tn = J dW / dt.
U = e + Ri donne i = (U-e) / R avec e = KW d'où i = (U-KW) / R.
Par suite : K U/R -K2W/R =J dW / dt.
J dW / dt + K2/R W = K U/R.
J R / K2 dW / dt + W = U / K. ( vitesse en régime permanent à vide U / K)
4,5 10-3 *2,7 / 1,22dW / dt + W =210 / 1,2 ; 8,44 10-3 dW / dt + W =175 ; dW / dt + 118,5 W =2,07 104.
Solution générale de cette équation : W = A exp(-118,5 t ) + 175 avec A une constante.
A t = 0; W =0 = A +175 d'où A = -175.
W = 175( 1-exp(-118,5 t)).
En
négligeant les pertes mécaniques, donner l'expression puis calculer la
vitesse maximale que peut atteindre la machine en fonctionnement moteur.
J R / K2 dW / dt + W = U / K. ( vitesse en régime permanent à vide U / K)
U/K = 210 / 1,2 = 175 rad/s.
|
Etude d'un variateur de tension.
Le
moteur étudié est alimenté par un convertisseur représenté ci-dessous.
les interrupteurs électroniques utilisés sont supposés parfaits. Ce
convertisseur est un variateur de tension destiné à faire varier la
vitesse du moteur à courant continu.
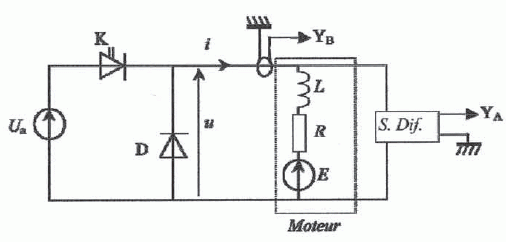
Le moteur peut-être modélisé par l'association série d'unn générateur
de tension idéale E, d'une résistance R = 2,7 ohms et d'une inductance
L. La force électromotrice obéit à la relation E = k n dans laquelle E
est exprimée en V et n en tr min-1. On donne k = 0,13 V min tr-1. La commande de l'interrupteur K est définie par :
0 < t < aT : K est fermé ; aT < t < T : K est ouvert.
T désigne la période de fonctionnement et a le rapport cyclique.
L'alimentation du montage est assurée par un générateur qui se comporte
comme une source de tension idéale délivrant une tension Ua = 205 V.
En charge, pour un certain régime de fonctionnement, on a relevé à
l'oscilloscope les variations de u et i. Pour cela on a utilisé une
sonde différentielle de tension de rapport 1/20 reliée à la voie A et
une sonde de courant de sensibilité 100 mV/A reliée à la voie B.
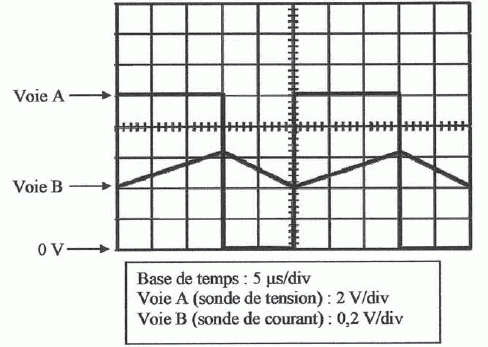
Déterminer la fréquence de fonctionnement f du convertisseur.
T = 5 *5 = 25 µs = 25 10-6 s ; f = 1/T = 1/25 10-6 =4 104 Hz.
Détermination de la tension moyenne délivrée par le convertisseur :
Donner la valeur de la tension u aux bornes du moteur pour 0 < t < aT.
5*2 = 10 V lu sur le graphe voie A ; rapport 1/20 de la sonde de tension d'où u = 10*20 = 200 V.
Donner la valeur de la tension u aux bornes du moteur pour aT < t < T.
u = 0 V.
Calculer la valeur moyenne <u> sur la période.
< u > = 200 a avec a = 0,6 ; < u > =120 V.
Déterminer la valeur moyenne <i> de l'intensité du courant absorbé par l'induit du moteur.
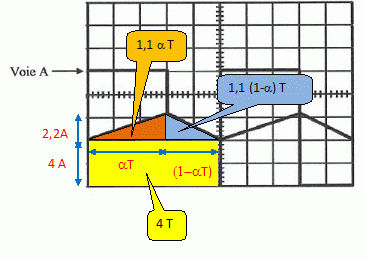
< i > = 4 +1,1 a +1,1(1-a) = 5,1 A.
Puissance consommée par la diode.
Indiquer un moyen de visualiser à l'oscilloscope le courant qui traverse la diode.
Mettre
un résistor de résistance R en série avec la diode et le générateur de
tension et visualiser la tension aux bornes de ce conducteur ohmique.
La tension aux bornes d'un conducteur ohmique et l'intensité qui le
traverse étant proportionnelles, l'image de la tension est l'image de
l'intensité au facteur R près.
Qu'appelle tension de seuil d'une diode ?
C'est la tension aux bornes de la diode à partir de laquelle celle-ci devient passante.
On considère que la tension de seuil est nulle.
Tracer
sur une période l'allure de la tension aux bornes de la diode et
l'allure du courant qui la traverse. Que peut-on dire du produit de ces
deux courbes ?
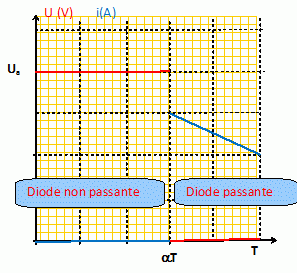
Le produit de ces deux courbes est nul. ( quand l'une est différente de zéro, l'autre est nulle )
On considère maintenant que la tension de seuil de la diode est constante et égale à 0,5 V.
Calculer la puissance moyenne consommée par la diode.
tension de seuil fois valeur moyenne de l'intensité qui traverse la diode.
0,5 * (1,1(1-a) +4) =2,2 W.
.
|
|