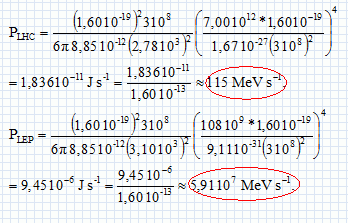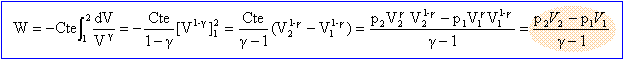Etude générale du LHC : rayonnement synchrotron, cryogénie, réfrigérateur réel : concours Capes  2011

Rayonnement synchrotron. Lorsqu'une particule est accélérée, elle émet un rayonnement électromagnétique que l'on nomme rayonnement synchrotron. ce rayonnement a de nombreuses applications en physique ou même en médecine. dans le cas d'un accélérateur, cette énergie perdue par rayonnement doit être compensée. Dans le cas du LEP, accélérateur d'électrons, ancêtre du LHC, cette perte d'énergie constituait une limite au développement de l'accélérateur. En est-il de même pour le LHC ? Cette partie propose de répondre à cette question. Justifier que le vecteur accélération du mouvement circulaire uniforme de la particule est non nul. Uniforme signifie : la valeur ( norme ) du vecteur vitesse est constante. Le vecteur vitesse est à chaque instant tangent à la trajectoire, circulaire dans ce cas. La direction du vecteur vitesse change ; en conséquence le vecteur vitesse n'est pas constant et la variation de ce vecteur vitesse n'est pas nulle. Le vecteur accélération est proportionnel à la variation du vecteur vitesse : le vecteur accélération n'est pas nul. Donner sans calcul, dans le cadre de la mécanique classique, la norme de l'accélération en fonction  de la vitesse v et du rayon  r de courbure dans le cas du mouvement circulaire uniforme. a = v2/r. L'accélération est-elle centrifuge ou centripète ? L'accélération est centripète, dirigée vers le centre du cercle. La puissance rayonnée dépend de la charge e de la particule, du rayon de courbure r de la trajectoire et des constantes c et e0. On supposera que la puissance rayonnée par une particule dans un mouvement circulaire est de la forme : P = K ea cb e0f  rg où K est sans dimension. Par analyse dimensionnelle, exprimer a, b, f et g. La puissance s'exprime en W, ou J s-1 ou V A ( volt ampère ). "e" est une charge en coulomb ou  une intensité fois une durée : A s. "c" est une vitesse en  m s-1 ; "r" est en mètre ( m) ;  est e0 s'exprime en A s V-1 m-1. Par suite :  V A = Aa sa  mb s-b Af sf V-f m-f mg = Aa+f sa+f-b  mb+g-f V-f . Par identification : f = -1 ; a+f = 1 soit a = 2 ; a+f-b=0 soit b = 1 ; b+g-f =0 soit g =-2. P = K e2 c e0-1  r-2 . K dépend  de la vitesse de la particule, on admet que : K =g4 ß4 /(6p). On note m la masse de la particule et E = gmc2 l'énergie de la particule. Montrer que pour v proche de c, la puissance rayonnée de la particule s'écrit : 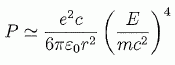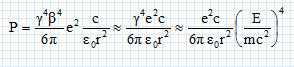A.N : pour un proton  : ELHC = 7,00 TeV ; rLHC = 2,78 km. 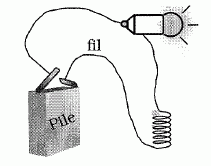pour un électron : ELEP = 108 GeV ; rLEP = 3,10 km.   On s'interesse dans la suite aux particules contenues dans un seul tube. On note N1 le nombre total de particules contenues dans ce tube et Tr la période de rotation de ces particules. Exprimer l'intensité moyenne du courant total I que l'on observe dans ce tube en fonction de N1, Tr et e. Intensité moyenne = charge / durée ; I = N1e /Tr. Montrer que la puissance totale rayonnée Pt par l'ensemble des particules d'un tube s'écrit  : Pt = IPD / (ec) ou D= 26,6 km est la circonférence du cercle parcouru par les particules de charge e dans le LHC ou le LEP. Pt = N1 P = ITr / e avec Tr = D / c d'où :  Pt =I P D / (e c). A.N : ILHC = 10,6 A ; ILEP =6,00 mA. PtLHC =1,06 *1,836 10-11 *26,6 103 / (1,60 10-19 *3,00 108) = 1,08 104 W. PtLEP =6,00 10-3 *9,45 10-6 *26,6 103 / (1,60 10-19 *3,00 108) = 3,14 107 W. PtLEP est environ 1000 fois plus grande que PtLHC. Cryogénie. Le choix a été fait au LHC de placer un grand nombre d'appareils à la température extrêmement basse de 1,9 K. cette température a été choisie pour  deux raisons principales : - l'alliage Niobium-Titane devient supraconducteur à cette température - l'hélium utilisé pour le refroidissement est superfluide : sa viscosité est quasi-nulle et sa capacité thermique très importante. Basses températures. Dans cette introduction, on présente certains effets des basses températures puis quelques notions de supraconductivité. Expérience qualitative : On réalise devant une classe de collège, le montage électrique schématisé ci dessous. Une pile électrique alimente une lampe. Le fil de connexion reliant la pile et la lampe est en cuivre et a été bobiné de manière a augmenter sa longueur. Le fil est placé dans l'air, la lampe brille de manière modérée Le fil est placé dans l'azote liquide, la lampe brille beaucoup plus. Indiquer quel est le paramètre  physique qui évolue lors de cette expérience. Interpréter cette expérience et proposer une explication microscopique. 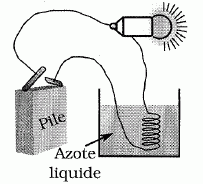Dans la seconde expérience, la résistance électrique du fil de cuivre plongé dans l'azote liquide diminue fortement ( l'intensité du courant sera plus élevée ). En conséquence la chute de tension provoquée par le fil est plus faible. La tension aux bornes de la lampe est plus élevée et celle-ci brille beaucoup plus. Un électron dans un métal se comporte pratiquement comme une particule libre. L'électron est repoussé par les autres électrons ( charges de même signe ), mais il est attiré par les ions positifs constituant le réseau cristallin. Cette attraction peut déformer ce réseau d'ions positifs de telle façon que d'autres électrons seront  attirés. Il en résulte des paires d'électrons qui se comportent comme des bosons : les paires se déplacent sans rencontrer la moindre opposition. Le élèves de collèges ne peuvent pas réaliser cette expérience en toute sécurité :  la température de l'azote liquide, proche de -200 °C  risquerait de provoquer de sévères gelures. Températures. Définir la température Celsius en fonction de la température thermodynamique exprimée en kelvin. Température kelvin = 273,15 + température Celsius. Proposer une méthode expérimentale simple permettant de mesurer la capacité thermique massique c d'un liquide. Dans un calorimètre de capacité thermique ( notée µ )connue, contenant une masse m de ce liquide, plonger une résistance électrique traversée par un courant d'intensité I. On relève la différence de température Dq au bout d'une durée Dt. Energie électrique consommée : RI2Dt. Energie électrique reçue par le calorimètre et le liquide : (µ + m c) Dq. Le système étant adiabatique : RI2Dt = (µ + m c) Dq. Pourquoi est-il important que l'hélium, utilisé comme fluide de refroidissement au LHC, ait une grande capacité thermique massique  et une viscosité quasi-nulle ? Une grande capacité thermique massique favorise les échanges thermiques entre le fluide hélium et les parties à refroidir. Une viscosité quasi-nulle permet au fluide de se déplacer dans les canalisations sans la moindre opposition. Supraconductivité : En quelle année a été découverte la phénomène de supraconductivité ? Quel matériau présentait alors cette propriété ? La supraconductivité fut découverte en 1911 par un physicien travaillant sur les propriétés du mercure à très basse température. Lorsqu'un matériau devient supraconducteur, on dit qu'il subit une transition de phase. Donner unn exemple de transition de phase, différent de celui-évoqué ci-dessus. Transformation d'un système thermodynamique lors d'un changement d'état physique (  fusion, ébullition, sublimation... ). La transition de phase entre un matériau ferromagnétique et paramagnétique se fait à la température Tc. Cette découverte est attribuée à Pierre Curie. Indiquer l'année approximative de cette découverte. Quels autres travaux peut-on associer à ce nom de famille ? Vers 1890 .Travaux en radioactivité, en piézoélectricité, en magnétisme. Quel est l'inconvénient principal des supraconducteurs actuels pour une utilisation dans la vie de tous les jours ? La supraconductivité ne se manifeste qu'à très basse température. Principe d'un système de refroidissement. Caractéristique d'un cycle ditherme réversible On considère un luide décrivant un cycle ditherme réversible entre une source chaude de température Tc et une source froide de température Tf. On note Qc ( respectivement Qf) le transfert thermique reçu par le fluide, pendant un cycle, de la part de la source chaude ( respectivement de la source froide ). Cette machine est un réfriférateur réversible, la source chaude est l'extérieur du réfrigérateur, la source froide est l'intérieur du réfrigérateur. Justifier que Qc< 0 et Qf > 0. Au cours d'un cycle le fluide reçoit le travail W , prend la chaleur Qf à la source froide (aliments à refroidir) et céde la chaleur Qc à l'extérieur, source chaude. Donner la définition de l'efficacité h d'un réfrigérateur, l'exprimer en fonction de Tc et Tf.  Au cours de ce cycle l'énergie interne du fluide est nulle : W + Qf + Qc= 0 avec Qc < 0 ; W et Qf >0 ; W = - Qf - Qc (1) d'aprés le second principe, l'entropie échangée est nulle sur le cycle : Qf / Tf + Qc / Tc =0. Qc= -Qf Tc / Tf . repport dans (1) : W= Qf [ Tc / Tf -1] efficacité = énergie thermique enlevée à la source froide divisée par le travail investi. Ce n'est donc pas un rendement h = Qf / W soit e = Tfroide / (Tchaude- Tfroide). Calculer h. Tc = 297 K ; Tf =277 K. h =277 /(297-277) =13,85 ~ 13,9. Régime permanent : En régime permanent,la température de la source froide reste constante, le fluide reçoit la puissance mécanique P1 =100 W. Calculer le transfert thermique moyen Qf1 reçu par la source froide de la part du fluide, pendant une durée de un jour ( notée Dt1). Q1 = h W = h P1 Dt1 =13,85 *100*24*3600 =1,99664 108 ~1,20 108 J ; Qf1 = -Q1. L'isolation de la source froide est imparfaite, elle reçoit de la part de l'extérieur une  puissance thermique Pperte. Calculer Pperte. En régime permanent , la puissance mécanique reçue par le fluide est utilisée pour compenser la puissance thermique reçue de l'extérieur. Pperte = P1 =100 W. Dans les mêmes conditions qu'à la question précédente, on place un volume V = 1,00 L d'eau  initialement à la température T0 = 297 K, dans le réfrigérateur réversible. On suppose que lamasse d'eau ajoutée est suffisamment petite pour considérer que la source froide garde une température constante Tf.  On constate que lors du refroidissement du volume V d'eau, la puissance mécanique moyenne reçue par le fluide vaut P2 = 103 W.  Capacité thermique massique de l'eau ceau = 4,18 kJ kg-1 K-1 ; reau = 1,00 103 kg m-3. Exprimer puis calculer la durée nécessaire Dteau pour que le volume d'eau atteigne la température Tf. Energie prélevée à l'eau : | Vreau ceau (Tf - T0 )| = h (P2-P1 ) Dteau. Dteau = | Vreau ceau (Tf - T0 )| /( h (P2-P1 )) =4180*20 /(13,85*3) =2,01 103 s. Etude d'un réfrigérateur réel. La machine comprend : un compresseur, un condenseur, un détendeur et un évaporateur. 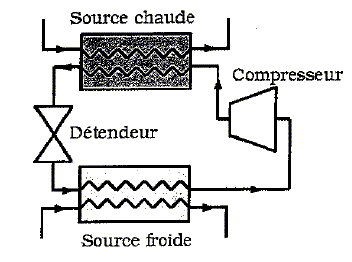Données sur l'ammoniac g= 1,31 ; M = 17,0 g/mol. Enthalpie massique de vaporisation à T1 =263 K : Dhvap(T1) =1300 kJ kg-1. Le fluide frigorigène est l'ammoniac. Il est considéré comme un gaz parfait  à l'état gazeux. Le fluide sort de l'évaporateur sous forme de vapeur juste saturante à l'état 1 : P1 = 2,9 bars et T1 = 263 K. Il subit dans le compresseur, une compression qui l'amène à l'état 2. La vapeur subit dans le condenseur une transformation à pression constante : refroidissement  jusqu'à la température T3a ( état 3a) puis liquéfaction totale ( état 3 ). Le liquide passe dans le détendeur et y subit une détente isenthalpique qui le ramène à la pression initiale P4=P1=2,9 bars et à la température T4 ( état 4). La vaporisation du liquide restant se termine dans l'évaporateur pour un  retour à l'état 1. 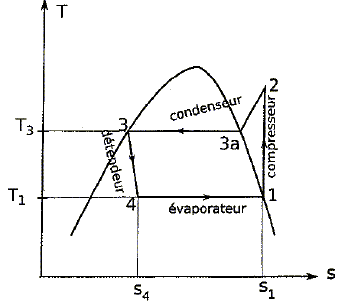Allure du diagramme entropique de l'ammoniac, l'entropie massique est placée en abscisse et la température en ordonnée. On a représenter la courbe d'équilibre liquide-vapeur et les étapes du cycle. Représenter l'allure de ce cycle  dans le diagramme de Clapeyron. état 1 2 3a 3 4 T(K) 263 T2 T3a T3 T4 P( bar) 2,9 10 10 10 2,9 x x1 x2 x3a x3 x4 S ( kJ K-1 kg-1) 5,76 5,76 - 1,42 1,45 h( kJ  kg-1) 1450 1620 1520 318 318 On note x la fraction massique de la vapeur, c'est à dire pour un système liquide diphasé liquide / vapeur : x = masse de vapeur / (masse de liquide + masse de vapeur ). Donner les valeurs numériques de x dans les états 1, 3a et 3. Le fluide sort de l'évaporateur sous forme de vapeur juste saturante à l'état 1 : x1 = 1. 3a se trouve sur la courbe d'équilibre liquide / vapeur : x3a = 1. Liquéfaction totale ( état 3 ) : x3 = 0. Calcul de T2 : Quelle est la variation d'entropie massique entre 1 et 2 ? Exprimer T2 en fonction de T1, P1, P2 et g. Calculer T2. D'apès le graphe T = f(S) : S1 = S2 : DS12 = 0. L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. Imaginer une transformation réversible passant de l'état initial à l'état final Transformation élémentaire : dS =dQ/T= (dU-dW)/T = Cv, m / T dT + P / T dV= R/(g-1) /T dT+ RdV/V Intégrer entre T1 et T2 : DS12 =  R / (g-1) ln(T2 /T1) + R ln(V2/V1)= 0 avec V2/V1 = T2P1 / (T1P2 ). g / (g-1) ln(T2 /T1) + ln(P1/P2)= 0. (T2 /T1)g / (g-1)(P1/P2) =1 ;  T2 = T1(P2/P1) (g-1)/g  =   263*(10 / 2,9)0,23664 = 352,5 ~353 K. Calcul de T3a. Exprimer la capacité thermique massique à pression constante cp de l'ammoniac en phase vapeur en fonction de g, R et la masse molaire M de l'ammoniac. cp/cv = g et m(cp-cv )=m/M R  ; cp-cp/g =R/M ; cp = R g/ (M  (g-1)). Exprimer T3a en fonction de la variation d'enthalpie massique entre les états 3 et 3a, en fonction de T2, M, R et g. Dh = cp( T3a- T2) ;  T3a = T2 + Dh /cp = T2 + Dh  M  (g-1) /(R g). T3a =352,5 +(1520-1620)103 *0,017*0,31 /(8,31*1,31) =352,5-48,4 =304,1 ~304 K. Pourquoi T3a est-elle égale à T3 ? La liquéfaction d'un corps pur à pression constante, s'effectue à température constante. Calcul de x4. Exprimer et calculer x4 en fonction de h4, h1 et Dhvap(T1). Détente isenthalpique : h4 = h3 ; vaporisation du liquide restant  : (mV+mL) ( h1-h4 )= mLDhvap(T1)   mL / (mV+mL) = ( h1-h4 ) / Dhvap(T1) ; x4 = mV /(mV+mL) = 1-mL /(mV+mL) x4 =1- ( h1-h4 ) / Dhvap(T1) = 1-1132 / 1300 = 0,13. Retrouver le résultat en exprimant x4 en fonction de s4, s1, T1 et Dhvap(T1). (mV+mL) ( s1-s4 )= mLDhvap(T1) / T1.   mL / (mV+mL) = ( s1-s4 )T1 / Dhvap(T1) ; x4 =1- ( s1-s4 ) T1/ Dhvap(T1) = 0,128 ~ 0,13. Grandeur utile massique : A quel niveau du cycle la "grandeur utile massique" est-elle échangée ? La source chaude est l'évaporateur :  h1-h4  = 1132 kJ kg-1. 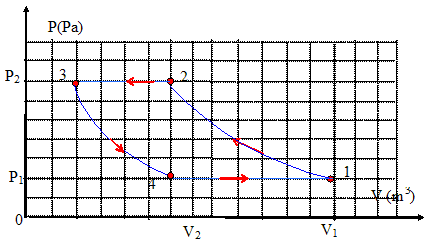Exprimer puis caluler le travail massique de compression en supposant la transformation adiabatique réversible. adiabatique 1-->2 : travail élémentaire des forces de pression -pdV avec p= Cte / Vg. intégrer entre V1 et V2. W12 =  nR(T2-T1) /(g-1) = m / M R(T2-T1) /(g-1) avec m = 1 kg. W12 =8,31/ 0,017 *(352,5-263) / 0,31 =141 kJ kg-1. Le système étant ouvert il faut prendre en compte le travail de transvasement  : Le fluide exerce une pression motrice à l'entrée du système et fournit le travail P1V1 ( par unité de masse ) que le compresseur n'aura pas à fournir. Le fluide exerce une pression résistante à la sortie du système et fournit le travail P2V2 ( par unité de masse ) que le compresseur devra fournir. W12 -P1V1 +P2V2 avec W12 =DU = U2-U1( système adiabatique ). U2-U1-P1V1 +P2V2 = U2+P2V2-U1-P1V1 = h2-h1 =1620-1450 =170 kJ kg-1. En déduire numériquement l'efficacité hr. hr = ( h1-h4)/W12 = 1132/170 =6,7. Calculer l'efficacité hc d'une machine frigorifique réversible fonctionnant avec une source chaude de température T3 et une source froide de température T1. Commenter. hc  = Tfroide / (Tchaude- Tfroide) =263/(304-263) =6,4. Les deux valeurs sont du même ordre de grandeur. Cependant l'efficacité théorique de Carnot devrait être supérieure à celle du cycle réel.

menu