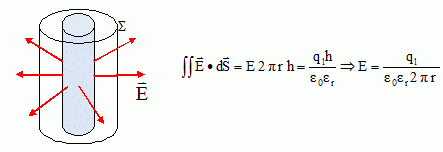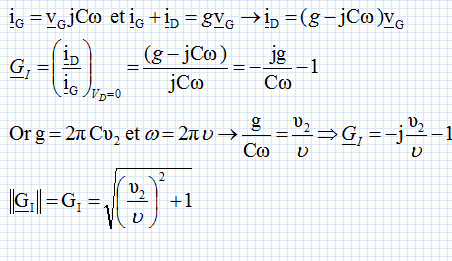Transistor à effet de champ à nanotube de carbone unique : concours Agrégation  2009

Un tel composant est constitué d'un nanotube de carbone déposé sur une surface isolante et en contact à ses deux extrémités avec deux électrodes métalliques ( appelées drain et source et notées respectivement D et S ). Le potentiel appliqué sur une troisième électrode, appelée grille et notée G, permet, grâce àun effet de champ, non décrit ici, de contrôler le courant électrique circulant dans le nanotube ( entre le drain et la source ). Dans la configuration étudiée ici, la grille est posée au dessus du nanotube, séparée de celuici par une fine couche isolante d'alumine. 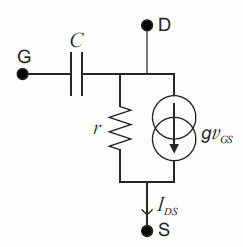L'objet de cette partie est l'étude électronique d'un tel transistor et de ses applications à la détection de charge ultra-rapide. 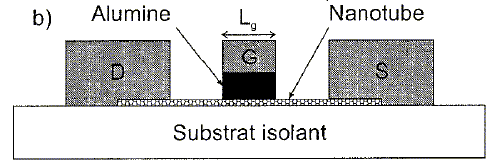Le dessin n'est pas à l'échelle. Les électrodes sont reliées aux instruments de mesure par un dispositif non représenté. Lors de son utilisation, le transistor est polarisé par des tensions continues de sorte que son schéma équivalent pour les petits signaux alternatifs est celui- représenté ci-dessous. 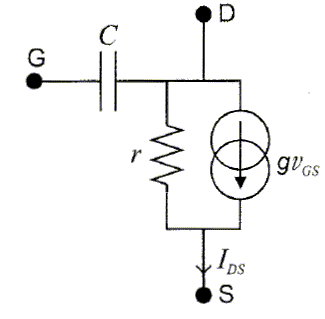Le générateur de courant est commandé par la tension entre la grille et la source. C est la capacité du condensateur formé par la grille, le nanotube et la couche d'alumine. r et g sont respectivement la résisatnce différentielle du nanotube ( entre le drain et la source ) et la trans-conductance du transistor définies par : 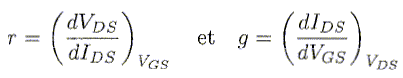où VGS = VG-VS et VDS = VD-VS, VD, VS étant respectivement les potentiels continus de la grille, du drain et de la source. IDS est le courant continu circulant dans le nanotube. uGS est la différence de potentiel alternative appliquée entre drain et source.  g, exprimée en siemens ( S), est le paramètre essentiel du transistor. c'est lui qui caractérise la variation du curant dans le nanotube lorsqu'on change la tension grille, à tension drain-source constante. Ordre de grandeur. Pour évaluer simplement un ordre de grandeur de la capacité C formé par la grille, le nanotube et la couche d'alumine, on modèlise l'ensemble par un condensateur cylindrique constitué de deux armatures coaxiales conductrices séparées par un diélectrique de permittivité relative er. Dans ce modèle, l'armature interne de rayon RNT est le nanotube. Elle est séparée de l'armature externe ( la grille) par une couche d'alumine d'épaisseur e. On suppose le condensateur infiniment long. On applique une différence de potentiel V entre les deux armatures. Quelle est la géométrie du champ électrique à l'intérieur du condensateur ? Représenter graphiquement les lignes de champ électrique. Tout plan contenant l'axe du cylindre est plan de symétrie et tout plan perpendiculaire à l'axe du cylindre est également plan de symétrie (cylindre infini) donc le champ est radial. Surface de Gauss : choisissons une surface fermée cylindrique S, de base circulaire, de même axe que C1 et C2, de longueur h et telle que le rayon r de sa base soit compris entre R1 et R2. On note ql, la charge par unité de longueur de l'armature interne.     Relier la tension V aux bornes du condensateur à la charge linéique ql. En déduire la capacité C par unité de longueur de l'ensemble nanotube-alumine-grille. 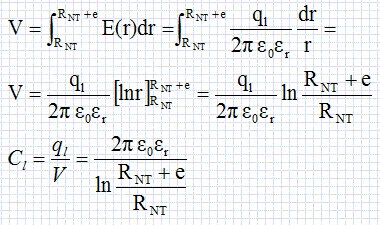A.N : er =9,8 ; RNT=0,5 nm ; e = 10 nm. Cl = 6,28*9,8*8,85 10-12 / ln(10,5 / 0,5) =1,8 10-10 F m-1 = 1,8 10-16 F µm-1 =180 aF µm-1 ; a = atto = 10-18. Longueur de la grille LG = 100 nm : C = Cl LG = 1,8 10-10* 10-7 = 1,8 10-17 F = 18 aF. Par la suite on prendra Cl =50 aF µm-1 ; Fréquences caractéristiques. En utilisant le schéma équivalent ci-dessus, montrer par analyse dimensionnelle que le NTFET possède deux fréquences caractéristiques : n1 = 1/(2prC) et n2 = g/(2pC). 2p est sans dimension ; rC est homogène à un temps ; 1/(2prC) est homogène  à l'inverse d'un temps, c'est à dire une fréquence. g, exprimé en siemensest l'inverse d'une résistance ; g/C est donc homogène à un temps et g/(2pC) est homogène  à l'inverse d'un temps, c'est à dire une fréquence. A.N : LG = 100 nm ; r = 100 kW ; g = 20 µS ; Cl =50 aF µm-1 ; C = Cl LG = 50 10-12 * 10-7 = 5 10-18 F. n1 = 1/(6,28 *105*5 10-18)= 3,2 1011 Hz. n2 = 20 10-6/(6,28*5 10-18)=6,4 1011 Hz. Comment ces fréquences dépendent-elles de la longueur de la grille LG ? n1 = 1/(2prCl LG) et n2 = g/(2pCl LG).  A g, r et Cl constants, si LG augmente, les fréquences diminuent. 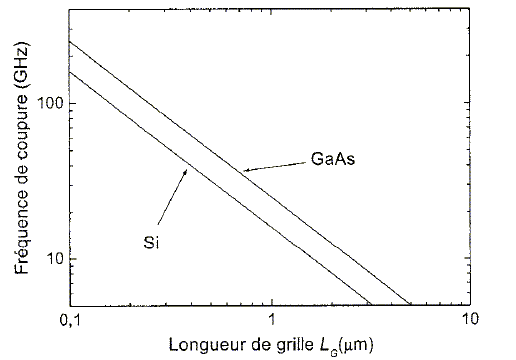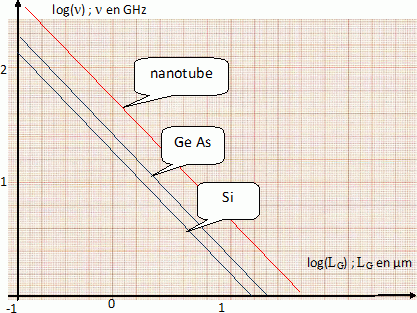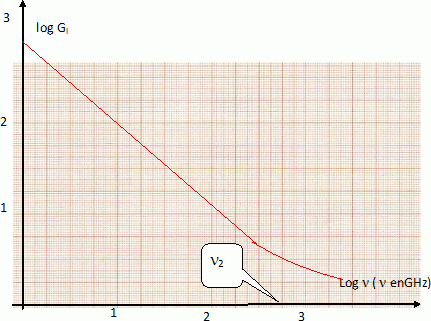On admet pour l'instant que la fréquence  n2 définit la fréquence maximale de fonctionnement du transistor. En utilisant la figure suivante, comparer la fréquence maximale de fonctionnement d'un NTFET à celle des transistors à effet de champ usuels à base de silicium ( ceux de vos ordinateurs) ou d'arséniure de gallium ( ceux de vos téléphones portables). Fréquence maximale d'utilisation des transistors à effet de champ usuels. Amplificateur à nanotube unique. On applique en plus des tensions de polarisation, une tension alternative vG de pusation w ( on notera n la fréquence correspondante ) sur la grille du transistor. On mesure la tension alternative vD entre drain et source et le courant iD qui circule dans une charge d'impédance Z branchée entre drain et source. Le schéma équivalent de ce montage pour les petits signaux alternatifs est présenté ci-dessous : 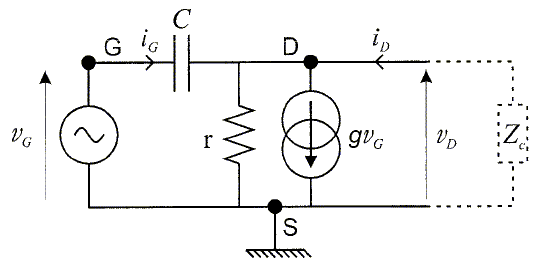Gain en tension : Gv = vD / vG avec iD = 0. Les grandeurs soulignées sont des nombres complexes. Exprimer Gv en fonction de r, C, g et w. vD = r ( iG - g vG ) soit : iG = vD / r + g vG. et vG = vD + iG /(jCw) soit : iG = ( vG - vD ) jCw. d'où : vD / r + g vG = ( vG - vD ) jCw. vD / r + vD jCw =  vG  jCw -g vG ; vD (1/r +jCw ) = vG  (jCw +g ) Gv = vD / vG =(jCw -g ) / (1/r +jCw ) = (jrCw -rg ) / (1 +jrCw ) or w =2pn et n1 = 1/(2prC) et n2 = g/(2pC)  ; n2  / n1 =rg. d'où : Gv =(j2prCn -rg ) / (1 +j2prCn ) = (jn / n1 -rg ) / (1 +jn / n1 )= (jn / n1 -n2  / n1 ) / (1 +jn / n1 ) Gv = (jn - n2 ) / ( n1 +jn ) 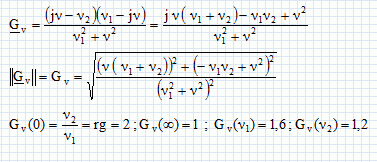 Représenter |Gv| en fonction de n pour LG =100 nm. Préciser le rôle des fréquences caractéristiques n1 et n2. Commenter les résultats obtenus. r = 100 kW ; g = 20 µS. 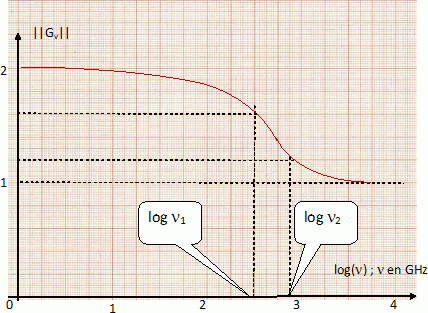n très inférieur à n1 ou n2 : le gain vaut 2, la capacité se comporte en circuit ouvert. n très supérieur à n1 ou n2 : le gain vaut 1, la capacité se comporte en circuit fermé. Montrer que le gain en tension  de l'amplificateur s'effondre si on branche une faible impédance Zc = 50 W entre drain et source. r et Zc sont en dérivation ; l'ipédance équivalente vaut : Z = r Zc /(r+Zc) ~Zc si r >> Zc. Dans le calcul précédent on doit donc remplacer r = 105 W par Zc = 50 W ; dans ce cas le gain aux basses fréquences devient gZc= 2 10-5*50 = 10-3. Le gain s'effondre. Montrer qu'on peut résoudre ce problème en connectant entre drain et source un grnd nombre de tube en parallèle. Soit n tubes en parrallèle :la résistance équivalente est r' = r / n et la conductance équivalente est g' = ng. Le produit rg est bien entendu inchangé, par contre la résistance équivalente r' diminue fortement si n est de l'ordre de 1000 et devient comparable à la valeur de Zc. Le problème précédent est alors résolu. Gain en courant. On définit le gain en courant GI par le rapport des courants iD et iG lorsqu'on court-circuite  drain et source ( ZC=0). Exprimer GI en fonction de C, g et w. vD=0, le conducteur ohmique r n'est traversé par aucun courant. Représenter GI en fonction de n avec une longueur de grille de LG = 100 nm. Si n << n2 : GI ~ n2 / n ; log GI ~log n2 -log n ; Si n >> n2 : GI ~1 ; log GI ~0 ; si n = n2 : log GI = ½ log 2. si n = 1 GHz  : log GI = log n2 =2,8. Le gain en courant est très grand à basse fréquence : la fréquence de coupure est n2 ; ce dispositif peut être utilisé comme amplificateur de courant. Application à la détection de charge. On cherche à utiliser le NTFET comme électromètre sensible et rapide. Le transistor est polarisé en continu et on s'interesse à la détection d'une petite variation de charge électrique de la grille par la mesure de la variation correspondante du courant dans le nanotube. On note NT le nombre d'électrons qui traverse le nanotube ( entre drain et source ) pendant la durée t. Exprimer NT en fonction de IDS, t et e en l'absence de perturbation sur la grille. IDS = NT e / t ; NT = IDS t /e. On impose une petite variation dq de la charge électrique de la grille. Montrer que NT varie de dNT =gdq t / (eC). On note q la charge portée par la grille : VGS = q/C+ VDS ~q/C ( q varie lentement par rapport à la fréquence ) dVGS ~dq/C ; dIGS ~g dVGS ~gdq/C ; De plus NT = IDS t /e ; dNT =dIGS t /e ; dIGS= dNT e /t. Par suite : gdq/C = dNT e /t soit : dNT =gdq t / (eC). Or n2 = g/(2pC) d'où : e dNT /(dq t ) =2pn2 .   A.N : n2 = 100 GHz ; dq=e ; t = 1 ns. dNT = 2pn2 dq t / e =6,28 1011  10-9  = 628 électrons. On cherche maintenant à comparer dNT aux fluctuations de NT associées au bruit du courant IDS. On admet qu'à basse température, celui-ci est dominé par le bruit de grenaille dû au caractère corpusculaire des électrons. Dans ces conditions les fluctuations de NT sont égales à DNT = NT½. Exprimer le rapport dNT / DNT en fonction de w2, t , IDS, e et dq. e dNT /(dq t ) =2pn2 = w2  ; dNT  = w2dq t /e et NT = IDS t /e ; DNT = NT½ = ( IDS t /e)½. dNT / DNT  =w2dq (t / (IDS e))½. Montrer que si on se fixe un rapport signal sur bruit minimum de 1, la plus petite charge dq que l'on peut déceler en un temps t est : dqmin = e C / g (IDS / ( t e))½. 1 = w2dqmin (t / (IDS e))½ ; dqmin =(IDS e / t )½ / w2 avec w2 = 2pn2 = g/C. dqmin =(IDS e / t )½ C /  g = e C / g (IDS  /(e t) )½. A.N : n2 = 100 GHz ; IDS  = 10 µA ; t = 1 ns. dqmin / e = 18 10-18 / 2 10-5 (10-5/ (1,6 10-19 10-9))½ = 0,23. L'électromètre est très sensible : il peut détecter en 1 ns, une charge inférieure à la charge élémentaire.

menu