|
L'EPR, un exemple de production d'énergie
sans émission de gaz à effet de serre :
concours agrégation interne 2010 |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
En quelle année la radioactivité a-t-elle été découverte et par qui ? En 1896, H. Becquerel découvre la radioactivité. Définir un noyau radioactif. Un noyau radioactif est un noyau instable dont la désintégration (destruction) aléatoire s'accompagne: l'apparition d'un nouveau noyau ; l'émission d'une particule notée a, b - ou b + ; l'émission d'un rayonnement électromagnétique noté g. Qu'appelle t-on radioactivité a, ß- et ß+ ? Qu'est-ce que le rayonnement g ? Un noyau expulse un noyaux d'hélium .( le noyau de l'atome d'hélium porte deux charges positives) Un noyau émet un électron noté : -10e. Uun neutron du noyau se transforme en proton. Un noyau artificiel (obtenu dans un réacteur nucléaire par exemple) émet un positon noté : 10e. Un proton du noyau se transforme en neutron Le noyau fils est souvent obtenu dans un état excité (niveau d'énergie élevé). Ce noyau dans cet état excité est en général noté Y*. Le noyau fils ne reste pas dans cet état instable. Il libère cette énergie excédentaire en émettant un rayonnement électromagnétique g. On a mesuré l'activité d'un échantillon contenant du radon 220 en opérant, toutes les 20 secondes, des comptages successifs d'une durée de 1 s. Les résultats du nombre n d'impulsions détectées par le compteur sont regroupés dans le tableau suivant :
La durée du comptage ( 1 s) est adaptée : elle est très inférieure à la demi-vie t½ ~50 s du radon. Dans une centrale nucléaire, on réalise la fission contrôlée de l'uranium 235. 23592U+10n --> 9438Sr + 140zXe+ x10n. Déterminer x et z en énonçant les lois de conservation. Conservation de la charge : 92 =38 + z d'où z = 54 ; conservation du nombre de nucléons : 235 +1 = 94+140 + x ; x = 2. Déterminer l'énergie libérée par cette fission en J et en MeV. On donne les masses m(23592U) = 234,99332 u ; m(9438Sr) =93,89446 u ; m(140zXe) = 139,89195 u ; m(10n)=1,00886 u ; c = 2,9979 108 m /s ; 1 u = 1,66054 10-27 kg ; 1 eV = 1,6022 10-19 J. Défaut de masse : Dm =m(9438Sr) +m(140zXe) + m(10n) -m(23592U) = 93,89446 +139,89195 +1,00886- 234,99332 =-0,19805 u Dm = -0,19805 *1,66054 10-27 = -3,28870 10-28 kg. Energie libérée : Dm c2 = -3,28870 10-28 *( 2,9979 108)2 = -2,9557 10-11 J ou -2,9557 10-11 / 1,6022 10-13 = -184,48 MeV. Quelle masse de pétrole libèrerait la même énergieque 1,0 kg d'uranium 235 ? Pouvoir calorifique du pétrole : 42 MJ kg-1 ; NA = 6,022 1023 mol-1. Quantité de matière d'uranium : n =1000 / 235 = 4,255 mol soit nNA = 4,255 *6,022 1023 =2,56 1024 noyaux d'uranium 235. Energie libérée par la fission de 1,0 kg d'uranium : 2,56 1024 * 2,9557 10-11 =7,574 1013 J = 7,574 107 MJ. Masse de pétrole libérant cette énergie : 7,574 107 /42 ~1,8 106 kg.
La température du circuit primaire. Soit le schéma simplifié d'un réacteur EPR ci-dessous : 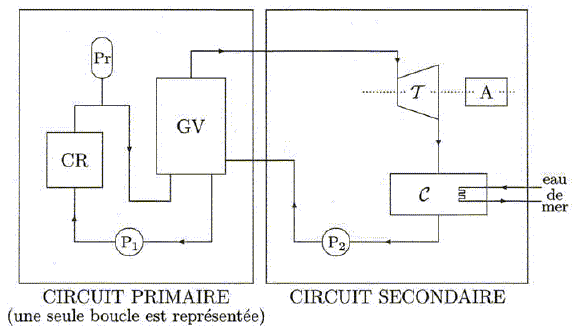 le circuit primaire comporte 4 éléments : le coeur situé dans la cuve du réacteur (CR), le pressuriseur (Pr), le générateur de vapeur ( GV) et la pompe primaire ( P1). Pour augmenter l'efficacité, une tranche nucléaire comporte 4 boucles parallèles comportant chacune un GV et une pompe P1. Les deux circuits primaire et secondaire sont fermés. Dans le cas de Flamanville 3, c'est de l'eau de mer qui joue le rôle de refroidissement du condenseur C. Dans le réacteur, la fission nucléaire produit une grande quantité de chaleur. l'eau aonsi chauffée circule dans le circuit primaire où elle est mise sous pression pour la maintenir à l'état liquide. Le circuit primaire chauffe le circuit secondaire par échange thermique. l'eau du circuit secondaire, propulsée par une pompe secondaire P2, se transforme en vapeur dans le générateur de vapeur. Elle fait tourner une turbine T couplée à un alternateur A qui produit de l'électricité. Le circuit secondaire comporte la partie secondaire du générateur de vapeur ( source chaude ), une turbine T, un condenseur C ( source froide ) et une pompe d'alimentation P2. Diagramme de Clapeyron du système liquide-vapeur de l'eau. Représenter l'allure du diagramme (P, V) de l'eau. Placer la courbe de saturation, le point critique, les domaines du liquide (L), de la vapeur (V) et du mélange liquide vapeur ( L+V). 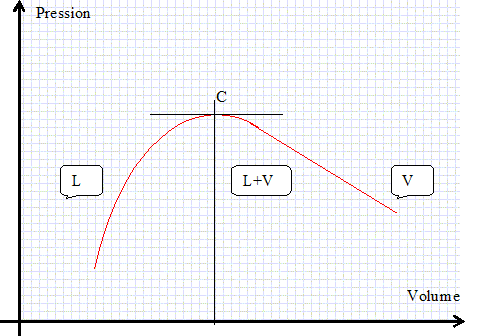 Modélisation du fonctionnement du circuit secondaire: cycle de Rankine. On raisonne sur m = 1 kg de fluide. La capacité thermique massique isobare du fluide liquide supposée constante est c = 4,18 kJ kg-1 K-1. Le coefficient de dilatation isobare a de l'eau liquide, supposé constant, est a = 1,5 10-4 K-1. Les transformations subies par l'eau sont les suivantes : A--> B : compression adiabatique réversible, dans la pompe d'alimentation, de la pression P1 = 0,05 bar à la pression P2 = 70 bar, du liquide saturant sortant du condenseur à la pression P1 ( point A). B --> D : échauffement isobare à P2 jusqu'à un point de vapeur saturante ( point E ). D --> E : vaporisation totale isobare à P2 jusqu'à un état de vapeur saturante ( point E ). E --> F : détente adiabatique réversible dans la turbine de P2 à P1 jusquà un état de mélange liquide vapeur ( point F). F --> A : liquéfaction totale isobare dans le condenseur à P1, de la vapeur présente en F. Représenter le cycle de Rankine dans le diagramme de Clapeyron. 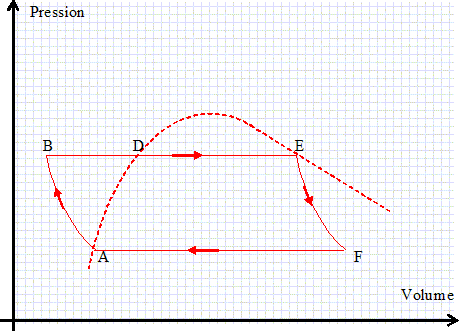 Dans le cas d'une transformation réversible élémentaire, établir : dh = cdT +(k+v)dP .( h : enthalpie massique du système) et ds = c/T dT+ k/T dP. ( s : entropie massique du système). dh =du + d(Pv) avec du = dq - Pdv ; dh = dq - Pdv +Pdv +vdP = dq +vdP ; de plus dq = cdT + kdP d'où dh = cdT +(k+v)dP. ds = dq /T = c/TdT + k/TdP. Etablir l'expression de k en fonction de T, v et a. dh et ds sont des différentielles totales exactes : 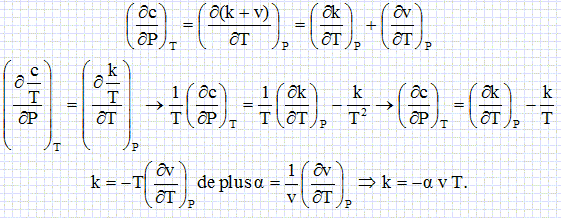
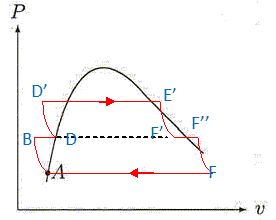
Dans toute la suite, on supposera que l'eau est incompressible. On donne son volume massique vl =10-3 m3kg-1. On note DT = TB-TA, l'augmentation de température du liquide dans la pompe d'alimentation. Compte tenu que DT <<TA, calculer DT à partir de l'expression de la variation d'entropie du système de A à B. On donne TA = 306 K. 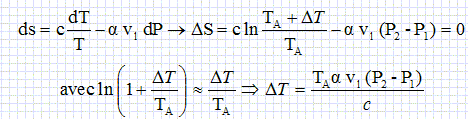 DT = 306*1,5 10-4*10-3 (70-0,05)105 / 4180= 0,08 K. Dans la suite du problème on considère que TA ~ TB. Calculer la variation d'enthalpie massique DhAB du liquide au cours de la compression AB. dhAB = cdT +(k+v)dP = cdT +v(1-aT)dP avec TA ~TB. DhAB =v(1-aT)(P2-P1) =10-3 (1-1,5 10-4 *306)(70-0,05) 105 =6674 ~6,7 kJ. Cette valeur est très faible par rapport aux autres énergies mises en jeu sur le cycle. On effectue le bilan enthalpique pour le fluide au cours du cycle. On néglige DhAB . Exprimer le travail massique W en fonction des enthalpies massiques du fluide à l'entrée et à la sortie de la turbine ( hE et hF). La variation d'enthalpie est nulle sur le cycle : 0 =DhAB + DhBE + DhEF +DhFA. 0 ~ 0+q2 +hF-hE +q1 ; hF-hE = -q1-q2 = W. On donne l'allure du cycle dans le diagramme de Mollier en coordonnées (h, s). L'intérêt de ce diagramme est que l'on peut lire directement les transferts d'énergie mis en jeu. Placer les points A, B, D, E, F. Justifier que la pente de (i) est supérieure à celle de (ii). Indiquer où se trouvent les grandeurs massiques W, q1 et q2. DhAB ~ 0 ; la transformation AB est adiabatique et réversible, donc DSAB = 0. La transformation EF est adiabatique et réversible, donc DSFE = 0. D et E sont situés sur la courbe de saturation. Les transformations DE et FA sont isobares : dP=0 et en conséquence dh = Tds+vdP = Tds dhDE = T2ds ; dhFA = T1ds ; h = f(s) sont des droites de pentes respectives T2 et T1 avec T2 >T1. 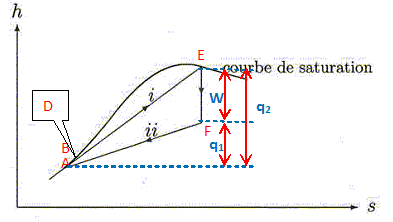 Calculer le rendement si W = -967 kJ kg-1 et q2 = 2561 kJ kg-1. h = |W| /q2 = 967/2561 =0,38. Optimisation du cycle. Au cycle précédent, on ajoute un surchauffeur (S) de sorte que le fluide sorte du générateur de vapeur ( GV) sous forme de vapeur surchauffée ( vapeur sèche ). Il est plus efficace d'utiliser deux turbines : une à basse pression ( TBP) et une à haute pression ( THP). Entre les deux on place un sécheur-surchauffeur (SS). Le sécheur-surchauffeur sépare le liquide de la vapeur etresurchauffe la vapeur à la sortie de THP de façon isobare. Il joue donc à l'entrée de TBP le même rôle que le surchauffeur du générateur de vapeur à l'entrée de THP. Sur la figure ci-après, R représente un réchaffeur. 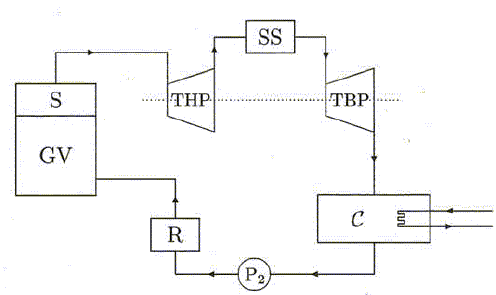 Les transformations subies par l'eau sont les suivantes : A--> B : compression adiabatique réversible, dans la pompe d'alimentation, du liquide saturant sortant du condenseur, de la pression P1 = 0,05 bar à la pression Pint inférieure à P2. B --> D : échauffement isobare dans le réchauffeur jusqu'au liquide saturant, à la pression Pint. D --> D' : compression adiabatique réversible du liquide saturant, de la pression Pint à P2 = 70 bar. D' --> E' : échauffement isobare à P2 du liquide dans GV, vaporisation totale isobare à P2 puis passage isobare dans le surchauffeur à P2. E' --> F' : détente adiabatique réversible dansTHP de P2 à Pint. En F' l'état du système est un mélange liquide vapeur proche de la vapeur saturante. F' --> F" :passage dans le sécheur-surchauffeur isobare à Pint. En F" l'état est la vapeur surchauffée ( vapeur sèche), proche de la vapeur saturante. F" --> F : détente adiabatique réversible dans TBP de Pint à P1. En F l'état est un mélange liquide vapeur. F --> A : liquéfaction totale isobare dans le condenseur à P1, de la vapeur présente en F.
|
|||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||
|
|