|
QCM
Physique : concours agrégation Algérie
2002 |
|||||||
|
|||||||
|
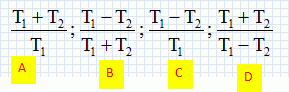
Un astronaute se sent " plus léger" sur la lune Est-ce à cause de : A. la nature du sol lunaire ; B. du manque d'atmosphère sur la lune ; C. de la faiblesse de la pesanteur g sur la lune ; D. de la rotation de la lune autour de la terre. Analyse : glune ~gterre / 6 ; le poids dépend du lieu où l'on se trouve ; il est 6 fois plus faible sur la lune que sur la terre. Les marées terrestres sont attribuées à la non uniformité, sur la surface de la terre, du champ de gravitation produit par tous les autres astres et en particulier la lune et le soleil. La contribution de chaque astre de masse M et distant de la terre de D est proportionnelle à : A. M / D2 ; B. M2 / D ; C. M / D3 ; D. M / D. Analyse : Expression de la force d'attraction gravitationnelle FT exercée par la Lune sur le corps de masse m. 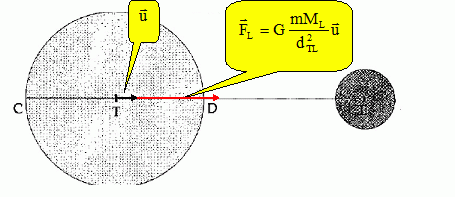 De même, on considère deux points C et D de la surface terrestre diamétralement opposés comme l'indique la figure. 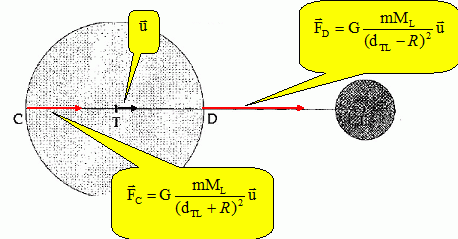 Le phénomène des marées est du à la différence des forces d'attraction : FC-FL en C et FD-FL en D. Donc C. Le champ de gravitation crée en un point P, par une sphère homogène de rayon R et de masse M, en fonction de la distance r du point au centre de la sphère, lorsque le point est extérieur à la sphère est : A. g(r) = -GM / r2 ; B. g(r) = -GM / r ; C. (r) = -GM / R2 ; D. (r) = -GM / r3. Analyse : Le champ de gravitation est inversement proportionnel au carré de la distance du point P au centre de la sphère. Donc A. La vitesse de libération Vl qu'il faut communiquer à un corps matériel situé à la surface d'une planète de rayon R et de masse M est : A. (GM / R)½ ; B.(2GM / R)½ ; C. (GM2 / R3)½ D. (2GM2 / R)½. Analyse : La particule est "libre" lorsque l'énergie mécanique est nulle. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. EM=½mv2-GMm / R =0 ; v =[2GM / R]½. Donc B.
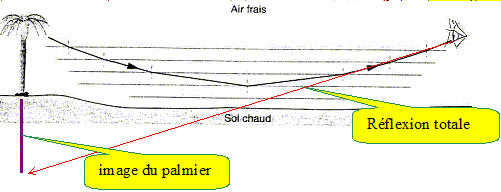
A. w2 g ( 2 z0 /g)½ cos l ; B. w g ( z0 /g2)1,5 cos l ; C. w g ( 2z0 /g)1,5 cos l ; D. w /g ( 2z0 /g2)½ tan l . Analyse : h : hauteur de chute ; w : vitesse angulaire de la terre et l : latitude à laquelle on effectue l'expérience. C. A. w0 ; B. w0(1-a2)½ ; C. w0(a2-1)½ ; D. w0(1+a2)½. Analyse : Les vecteurs sont écrits en gras et en bleu. On note f = -m v la force de frottement fluide, où m est une constante et v le vecteur vitesse de la masse en translation. mg-kx-mv= m d²x/dt² ; m d²x/dt² +mv + k x=0 avec v = dx/dt = x' ; m d²x/dt² +mx' + k x=0 (1) (1 ) peut s'écrire : d²x/dt² +m/ m x' + k/ m x=0. or w20 = k/m et on pose 2l= m /m ; d'où : d²x/dt² +2l x' + w20 x=0 (2) équation caractéristique r2+2l r + w20 =0 ; discriminant D = 4l2-4w20. On pose W2 =w20 -l2; W = [w20 -l2]½ = [w20 -µ2/ (4 m2)]½ ; donc B. L'effet mirage est dû à : A. la dispersion de la lumière par l'atmosphère ; B. la diffraction de la lumière par les couches atmosphériques ; C. l'interférence lumineuse au niveau du sol ; D. au gradient d'indice de réfraction résultant de la variation de la température au niveau du sol. Analyse : Réfraction : dans un milieu hétèrogène la lumière ne se propage pas en ligne droite.
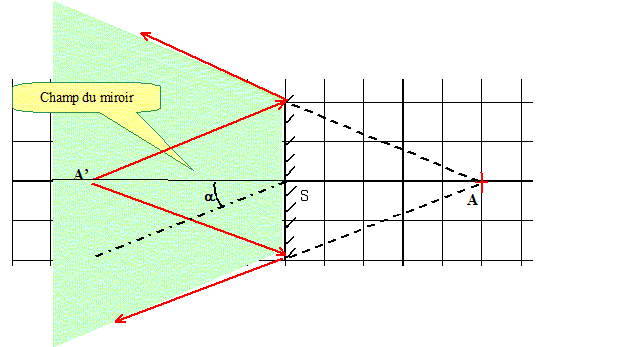
L'arc en ciel est dû à : A. la réflexion de la lumière par l'atmosphère ; B. la dispersion de la lumière par les gouttes d'eau de l'atmosphère ; C. la rotation de la terre autour d'elle même ; D. la rotation de la terre autour du soleil. Analyse : L'arc-en-ciel naît des réflexions et réfractions de la lumière du soleil à travers les gouttes d'eau dans les nuages. On représente une goutte d'eau par une sphère d'indice n = 1,33. L'observateur voit l'ensemble des lumières réémises par toutes les gouttes constituant le nuage. Donc B. 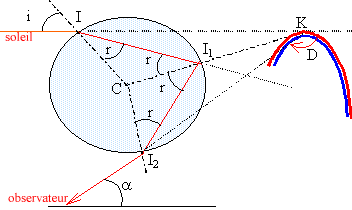 A. la diffusion Rayleigh ; B. la diffusion Compton ; C. la diffusion Raman ; D. la diffusion Thompson. Analyse : La lumière diffusée par l'atmosphère est 16 fois plus riche en radiations bleues qu'en radiations rouges. Un mélange de violet, de bleu, de vert et une toute petite fraction des autres couleurs, diffusés donne la couleur bleue. ; donc A. A. miroir plan ; B. miroir sphérique convexe ; C. miroir sphérique concave ; D. miroir parabolique. Analyse : Champ du miroir plan :
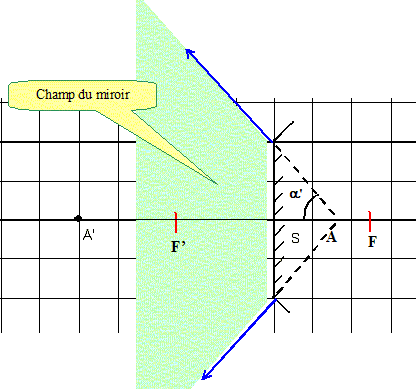
Champ du miroir sphérique convexe :
donc B.
Une source S se déplaçant à la vitesse U émet un son ( des " bips " ) de fréquence N. Un auditeur se déplaçant à la vitesse U' dans le même sens et la même direction que la source perçoit le son à la fréquence N' telle que : ( V célérité du son ) A. N' = (V+U') N / (V+U) ; B. N' = (V-U') N / (V-U) ; C. N' = (V+U') N / (V-U) ; D. N' = (V-U') N / (V+U). Analyse : Les vitesses seront comptées positives dans la direction de propagation du signal (de l’émetteur vers le récepteur). Le bip se propage à la célérité V dans l'air. A l'instant initial (t = 0), la source (distante de d1 du point O, auditeur) émet son premier bip. A quel instant t1 l'auditeur reçoit-il le premier bip ? t1 = d1/(V-U'). La source émet, tout en se déplaçant, des bips régulièrement avec une période T. A quelle distance d2 de l'observateur se trouve la source lorsqu'elle émet son deuxième bip ? d2 =d1 - (U+U')T. A quel instant t2 l'observateur reçoit-il son deuxième bip ? t2 =T+ d2/ (V-U') =T - (U+U') / (V-U') T + t1. Relation entre la période T' des bips reçus par l'observateur et la période T des bips émis pas la source. T' = t2-t1= (1 - (U+U') / (V-U') T ; T' = (V-U) / (V-U') T La fréquence est l'inverse de la période : N' =(V-U') / (V-U) N ; donc B. D'après le théorème de gauss : A. la circulation du vecteur champ électrique le long d'un contour fermé est nulle ; B. la circulation du vecteur champ électrique entre deux points A et B est indépendant du cemin suivi ; C. le flux du vecteur champ électrique à travers une surface fermée est nul ; D. le flux du champ électrostatique crée par une distribution de charge, à travers une surface fermée quelconque, est proportionnel à la charge totale intérieure à cette surface. Analyse :
Un conducteur cylindrique est constitué de deux cylindres coaxiaux de rayons R1 et R2 de hauteur L et portant sur leurs surfaces en regard les charges +Q et -Q. La capacité du condensateur est : A. 2p e0 L log (R2/R1) ; B. 2p e0 /L log (R1/R2) ; C. 2p e0 L / log (R2/R1) ; D. p e0 / (L log (R2/R1)). Réponse C. Dans le cas le plus général, la force de Lorentz exercée sur une charge q a pour expression : 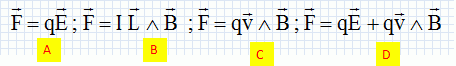 Réponse D. D'après la loi de Biot et Savart : A. le champ magnétique entre les branches d'un aimant en U est uniforme ; 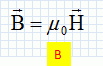 ; ; 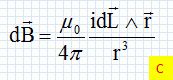 ; ;
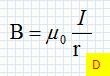 . . Réponse C. La fréquence des oscillations entretenues d'un dipôle RLC série est : A.la fréquence de la tension excitatrice ; B.égale à 2 pi ( LC)½ ; C. d'autant plus petite que la résistance R du circuit est plus grande ; D. d'autant plus élevée que l'inductance L et la capacité C sont plus petites. Analyse : f = 1 / (2pi (LC)½) ; donc D. Les amplificateurs opérationnels peuvent servir à réaliser des montages ? A. amplificateurs de courants électriques ; B. amplificateurs de tensions électriques ; C. adaptateurs d'impédances ; D. comparateurs d'intensités de courants électriques. Réponse B.
|
|||||||
| |
|||||||
|
|
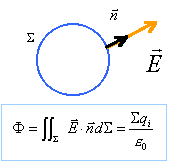
 d
d