Isolation d'une façade vitrée, hydrodynamique, chimie de la chaux : BTS Enveloppe du bâtiment 2011.

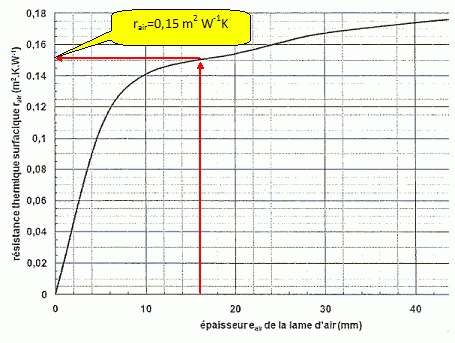
Isolation d'une façade vitrée, hydrodynamique, chimie de la chaux : BTS Enveloppe du bâtiment 2011. La vitrine du commerce a une longueur L = 20,0 m et une hauteur H = 3,00 m. Amélioration de l'isolation de la façade vitrée. Résistance thermique surfacique intérieure : rsi = 0,125 m2KW-1. Résistance thermique surfacique extérieure : rse = 0,0435 m2KW-1. Température intérieure : qi = 20,0°C ; température extérieure : qe = 3,00°C. Dans un premier temps, on s'intéresse au bilan thermique de l'existant. Le vitrage actuel est un vitrage simple d'épaisseur eS =8,00 mm, constitué d'un verre plat de conductivité thermique l =1,00 W m-1K-1. Exprimer puis calculer la résistance thermique surfacique rS de ce vitrage. rS = rsi + rse + eS / l = 0,125 +8,00 10-3 / 1 + 0,0435 =0,17648 ~0,176 m2 K W-1. Donner l'expression de la densité de flux thermique  fS à travers ce vitrage. Calculer fS. Flux thermique surfacique fS=1/rS(qi -qe) =1/0,17648 (20-3) =96,33 ~96,3 W m-2. Donner l'expression du flux thermique  JS à travers ce vitrage. Calculer JS. Flux thermique  JS= fS L H =96,33*20*3 = 5779,8 ~5,78 103 W. Remplacement du simple vitrage par un double vitrage. Les deux solutions techniques proposées par le fournisseur exploitent un verre de conductivité thermique l =1,00 W m-1K-1. Dans les deux cas, la lame d'air entre les deux épaisseurs de verre a pour épaisseur eair = 16,0 mm et pour résistance thermique surfacique rair. Cas 1 :  double vitrage symétrique  ( de type 4-16-4). Les deux épaisseurs de verre sont identiques et égales à e = 4,00 mm. Cas 2 :  double vitrage asymétrique  ( de type 10-16-4). Les deux épaisseurs de verre sont respectivement e1= 10,0 mm ( verre extérieur ) et e2 = 4,00 mm ( verre intérieur ). Etablir l'expression des résistances thermiques surfaciques r ( double vitrage symétrique) et r' ( double vitrage asymétrique ) de ces deux vitrages. r = rsi + rse + 2e / lverre +eair / lair ; r' = rsi + rse + (e1 +e2)/ lverre +eair / lair ; Le graphique suivant donne la variation de la résistance thermique surfacique rair de la lame d'air ( supposée immobile ) en fonction de son épaisseur eair. Déterminer graphiquement rair. Calculer r et r'. r = rsi + rse + 2e / lverre +rair = 0,125 + 0,0435 + 0,008/1 + 0,15 =0,3265 ~0,327 m2 K W-1. r' = rsi + rse + (e1 +e2)/ lverre +rair =0,125 + 0,0435 + 0,014/1 + 0,15 =0,3325 ~0,333 m2 K W-1. Exprimer puis calculer les densités de flux thermique f et f' à travers les vitrages. Flux thermique surfacique f =1/r(qi -qe) =1/0,3265(20-3) =52,067 ~52,1 Wm-2. f '=1/r(qi -qe) =0,3325(20-3) =51,1278 ~51,1 Wm-2. On étudie les températures de surface pour un vitrage simple. Exprimer puis calculer les températures de surface intérieure et extérieur. f =1/rsi(qi -qi s) ; qi s=qi - f rsi =20-96,33*0,125 = 7,98°C. f =1/rse(qe s -qe) ; qe s=qe + f rse = 3+96,33*0,0435 =7,18°C. Représenter l'allure de profil  de température de part et d'autre et à l'intérieur de la vitre simple. 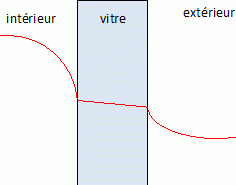Les températures de surface intérieure et extérieure pour les deux types de doubles vitrages sont respectivement 13,5 °C et 5,30 °C. Conclure quand à l'intérêt d'un double vitrage. Un double vitrage diminue les pertes thermiques d'environ 45 % par rapport à un simple vitrage. De plus la température de surface intérieure est de l'ordre de 15°C au lieu de 8°C : il y a moins de risque de condensation dans le cas du double vitrage Le double vitrage asymétrique permet une meilleur isolation phonique que le double vitrage symétrique. Vérification de la ventilation. Diamètre de la canalisation du système de ventilation : d = 15,0 cm ; rair = 1,20 kg m-3 ; rmercure= 13,6 103 kg m-3 ; g = 9,81 m s-2. Un tube de Pitot est muni en A d'une prise de pression à point d'arrêt et en B d'une prise latérale de pression. Les points A et B sont sur la même ligne de courant. En A vA=0 et en B la vitesse d'écoulement est vB par rapport au tube de Pitot. 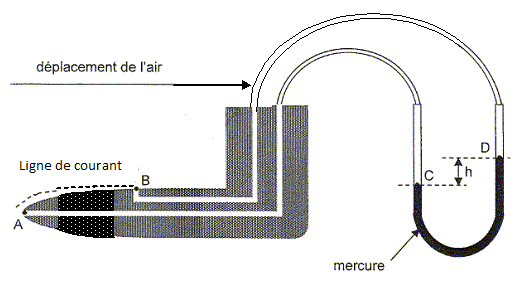La différence de pression entre les points A et B induite par la différence de vitesse entre ces points est intégralement transmise au mercure dans un tube en U de section constante jouant le rôle de manomètre différentiel. L'air entre A et C et entre B et D est au repos. On a donc PC = PA et PD = PB. Rappeler la loi fondamentale de la statique des fluides. Dans un fluide homogène au repos, la différence de pression entre deux points A et B vaut : PB-PA = rfluide g ( hB-hA) avec hB-hA la différence d'altitude entre A et B. Etablir une relation entre PA, PB, rmercure, g et h. PC-PD =PA-PB = rmercure g  h. Les points A et B sont à la même altitude. 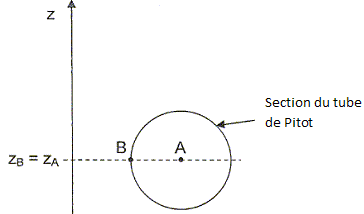En appliquant le théorème de Bernoulli le long de la ligne de courant entre A et B, exprimer la variation de pression PA-PB en fonction de vB et rair. relation de Bernoulli : ½(VB2-VA2)+ g(zB-zA)+( PB-PA)/rair =0. ½VB2+( PB-PA)/rair =0. PA-PB= ½rairVB2. Montrer que h = ½rairVB2 / (rmercure g). PA-PB= ½rairVB2 ; PA-PB = rmercure g  h ;  ½rairVB2 = rmercure g  h ; h = ½rairVB2 / (rmercure g). En déduire l'expression de h en fonction de rair, rmercure,  du débit volumique dans la canalisation Qv et de son diamètre d. Section de la canalisation S = 0,25 p d2 ; Qv = S VB ; VB =Qv / (0,25 p d2). h = ½rair (Qv / (0,25 p d2))2 / (rmercure g). Les masses volumiques, le diamètre d sont connues ; h est mesuré : un tel dispositif permet donc de déterminer la valeur du débit volumique. Calculer h.Qv = 75,0 m3 h-1 = 75,0 / 3600 m3 s-1 = 0,02083 m3 s-1. h = 0,5*1,20 (0,02083 / (0,25 *3,14 *0,152))2 / (13,6 103*9,81)= 6,26 10-6 m. Le remplacement du mercure par un autre fluide permettrait-il d'améliorer la sensibilité de l'appareil ? La masse volumique du fluide apparaît au dénominateur dans l'expression de la hauteur h. Oui, car la masse volumique d'un autre fluide est inférieure à celle du mercure ( pour l'alcool ~800 kg m-3 ). Quelques aspects de la chimie de la chaux. On donne les masse atomiques molaires en g/mol : M(H) = 1 ; M(C) =12 ; M(Ca) = 40 ; M(O) = 16 ; Vm = 24,0 L/mol ; Capacité thermique de l'eau C = 4,18 103 J Kg-1 K-1. Chaleur latente de vaporisation de l'eau L=2,25 106 J kg-1. La chaux vive ( principalement constituée d'oxyde de calcium CaO ) est une poudre blanche obtenue par décomposition thermique ( ou pyrolyse ) du calcaire ( de formule CaCO3 ) aux environs de 900°C. Cette pyrolyse produit un dégagement de dioxyde de carbone. CaCO3 (s)--> CaO(s) + CO2(g). (1) Calculer la quantité de matière de CO2 obtenue par pyrolyse de m=1,00 kg de calcaire : n(calcaire) = m / M avec M = 40+12+3*16 = 100 g/mol ; n(calcaire) = 1000 / 100 = 10,0 mol. D'après les nombres stoechiométriques de (1) : n(calcaire) = n(CO2) = 10,0 mol. En déduire le volume V de dioxyde de carbone produit. V = n(CO2) Vm = 10,0 * 24,0 = 240 L. La chaux éteinte ( Ca(OH)2 ) est obtenue par réaction de la chaux vive avec de l'eau. Ecrire l'équation bilan de la réaction. CaO(s) + H2O(l) = Ca(OH)2. (2) Calculer la masse d'eau tout juste nécessaire à l'hydratation de 1,00 kg de chaux vive. n(CaO) = m(CaO) / M(CaO) = 1000 / (40+16) = 17,857 mol. D'après les nombres stoechiométriques de (2) : n(eau) = n(CaO) = 17,857 mol. m(eau) = n(eau) M(eau) = 17,857 * 18,0 =321,43 ~321 g. En cas de mélange de grandes quantités de chaux vive et d'eau, la chaleur dégagée ( Q = 1155 kJ pour 1 kg de chaux vive ) est telle que l'eau peut se mettre à bouillir et projeter de la chaux vive qui est corrosive. On considère une masse d'eau m', initialement à q1 = 20,0°C, que l'on suppose portée à ébullition ( qf = 20,0°C ) grâce à la chaleur dégagée par l'extinction de la chaux vive. Quelle est la masse m' si on éteint 1 kg de chaux vive ? Energie nécessaire pour porter une masse m' d'eau de 20 °C à 100°C, l'eau restant liquide : Q1 = m' C (qf-q1). Energie nécessaire pour vaporiser une masse m' d'eau à 100 °C : Q2 = m' L. Q1 + Q2 = m'( L + C (qf-q1)) = Q m' = Q / ['( L + C (qf-q1))]= 1155 103 / ( 2,25 106 +4180*80) =0,447 kg. La masse d'eau est importante, une grande quantité de chaux vive peut être projetée : il faut porter des gants, des lunettes de protection et un bleu de travail.

menu