Autour de l'eau oxygénée : bts chimiste 2011.

Calcul d’une énergie de liaison. Du peroxyde d’hydrogène ou « eau oxygénée » peut être obtenu lors de la combustion du dihydrogène dans le dioxygène suivant la réaction : H2(g) + O2(g) --> H2O2(g). Écrire les formules de Lewis de H2, O2, H2O et H2O2.   Écrire l’équation de la réaction de formation de H2O liquide. ½O2(g) + H2(g) = H2O(l). Calculer l’enthalpie standard de formation de H2O gaz, à 298 K. DrH° =DfH°(H2O(l)) -0,5 DfH°(O2(g))-DfH°(H2(g))=-285,8 kJ /mol. H2O(l) = H2O(g). DvapH° = 40,7 kJ/mol. DvapH° =DfH°(H2O(g))-DfH°(H2O(l)) d'où DfH°(H2O(g))= DfH°(H2O(l))+DvapH° = -285,8+40,7 = -245,1 kJ/mol. On rappelle que l’énergie d’une liaison correspond à l’énergie (assimilée à une enthalpie) qu’il faut fournir pour casser cette liaison, tous les composés étant pris à l’état gazeux. Calculer l’énergie de la liaison O-H. ½O2(g) + H2(g) = H2O(g). DfH°(H2O(g)) =½ElO=O + ElH-H-2 ElO-H  ; ElO-H  = 0,5 [½ElO=O + ElH-H-DfH°(H2O(g)) ]=0,5[491*0,5 +435 +245,1]= 462,8 kJ/mol. Calculer l'énegie de la liaison O-O dans la molécule de peroxyde d'hydrogène. H2(g) + O2(g) --> H2O2(g) DfH°(H2O2(g)) =ElO=O + ElH-H-2 ElO-H -ElO-O ; ElO-O  = ElO=O + ElH-H -2 ElO-H -DfH°(H2O(g)) ]=491 +435 -2*462,8+139,4=139,8 kJ/mol. étude de la structure d’un solide ionique L’eau oxygénée peut être également préparée en traitant du peroxyde de baryum BaO2 par de l’acide sulfurique. Le peroxyde de baryum est obtenu par action du dioxygène sur l’oxyde de baryum BaO, solide ionique dont la structure est étudiée ici. Donner la structure électronique de l’ion Ba2+. 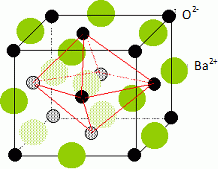1 s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p6. L’oxyde de baryum solide possède la même structure cristalline que le chlorure de sodium : les ions oxyde O2- forment une structure cubique faces centrées, les ions Ba2+ occupent la totalité des sites octaédriques. Compléter la maille conventionnelle de l’oxyde de baryum, en utilisant deux couleurs distinctes pour les éléments Ba et O respectivement.  La masse volumique de l’oxyde de baryum est ρ = 5,90 kg.dm-3, le rayon ionique de l’ion oxyde est égal à 0,140 nm. Calculer le rayon ionique de l’ion Ba2+. La maille compte en propre 4 motifs BaO. Masse de la maille : 4 * masse molaire BaO (kg/mol) / nombre d'Avogadro. Masse = 4*153 10-3 / 6,023 1023 = 1,016 10-24 kg. Volume de la maille a3. (en m3) Masse volumique (kg/m3 )=5900 = 1,016 10-24 / a3. a3 = 1,016 10-24 / 5900 =1,72 10-28 m3 ; a = 5,56 10-10 m. Les ions sont considérés comme des sphères en contact : la longueur de l'arète est égale à deux fois la somme des rayons ioniques. a= 2*(1,40 +rBa2+ ) 10-10 = 5,56 10-10 m ; rBa2+ =1,38 10-10 m = 0,138 nm.   Etude thermodynamique de la dismutation de l’eau oxygénée Donner la valeur du nombre d’oxydation de l’atome d’oxygène dans O2, H2O2 et H2O. Dans O2 : n.0(O) = 0 ; dans H2O2, n.o(O) = -1 ; dans H2O, n.o(O) = -2. Vérifier que le potentiel standard du couple H2O2(aq)/H2O(l) vaut 1,77 V. E°(O2(g) / H2O(l)) = 1,23 V. E°(O2(g) / H2O2(aq))= 0,69 V. (1) ½O2(g) +2H+aq + 2e- = H2O(l) ; DG°1 =-2FE°(O2(g) / H2O(l)). (2) O2(g) +2H+aq + 2e- = H2O2(aq) ; DG°2 =-2FE°(O2(g) / H2O2(aq)). (3) H2O2(aq) + 2H+aq + 2e- =2 H2O(l). DG°3 =-2FE°(H2O2(aq)/H2O(l)). 2 fois (1) -(2) donne (3) : -4 FE°(O2(g) / H2O(l)) + 2 FE°(O2(g) / H2O2(aq)) = -2FE°(H2O2(aq)/H2O(l)). E°(H2O2(aq)/H2O(l)) = 2 E°(O2(g) / H2O(l)) -E°(O2(g) / H2O2(aq)) =2*1,23-0,69 = 1,77 V. En déduire que, au moins à pH = 0, l’eau oxygénée se dismute. écrire l’équation de la réaction de dismutation faisant intervenir une mole de H2O2 et définir la constante de réaction correspondante K°. 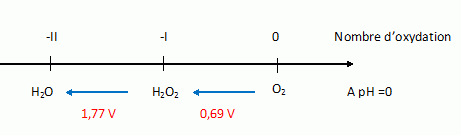Il y a dismutation d'une espèce si celle-ci est écrite à droite d'une autre espèce avec un potentiel inférieur : (4) H2O2(aq) =½O2(g) + H2O(l). K° =P½O2 / [H2O2(aq)]  Calculer K° à 298 K. 0,5 fois(3) -0,5 fois(2) donne (4) : DG°4 =0,5 (DG°3 -DG°2 ) =0,5(-2F*1,77 +2F*0,69) =F(-1,77+0,69) = -1,08 F. de plus DG°4 = -RT ln K° ; ln K° =1,08 F/(RT) = 42. K° =1,7 1018. Déterminer la concentration en peroxyde d’hydrogène à l’équilibre en supposant que PO2=1,0 bar. Conclure. Expliquer pourquoi il est cependant possible de trouver au laboratoire des solutions aqueuses d’eau oxygénée. [H2O2(aq)] =P½O2 / K° =1 / 1,7 1018 =5,7 10-19 mol/L. La constante de réaction étant très grande, la réaction est totale( thermodynamiquement spontanée ). Cette réaction étant très lente, du fait d'un blocage cinétique, on peut trouver des solutions aqueuses d'eau oxygénée dans un laboratoire. L’eau oxygénée, au laboratoire, peut être utilisée comme oxydant ou comme réducteur. Écrire l’équation de la réaction de l’eau oxygénée avec le permanganate de potassium en présence d’acide sulfurique. 2 fois { MnO4- + 8H+ + 5e- = Mn2+ + 4H2O } réduction 5 fois {H2O2 = O2 + 2H+ + 2e- } oxydation 2 MnO4- + 5 H2O2 + 6H+ = 5 O2 + 2 Mn2+ + 8H2O. Écrire l’équation de la réaction de l’eau oxygénée avec les ions iodure en solution aqueuse. Proposer un mode opératoire de dosage de l’eau oxygénée utilisant cette dernière réaction en précisant la préparation de l’échantillon, le choix du réactif titrant ainsi que le repérage de l’équivalence. Les deux demi-équations d'oxydo-réduction correspondant aux couples envisagés : 2I- =I2 + 2e- oxydation H2O2 +2e- +2H3O+= 4H2O réduction L'équation bilan de la réaction : H2O2 + 2I- +2H3O+= 4H2O + I2. Equation bilan du dosage du diiode formé par le thiosulfate : 2S2O32- = S4O62-+2e- oxydation ; I2+2e- =2I- réduction 2S2O32- + I2 = S4O62- + 2I- d'où n(I2) =½n(S2O32-). Indicateur de fin de réaction : en présence de diiode, l'empois d'amidon donne une couleur violette foncée. Une eau oxygénée est dite à « v volumes », si un litre de cette solution dégage par décomposition complète, en eau et en dioxygène, v litres de dioxygène, à 0 °C et sous une pression de 1,013 bar. Calculer, en mol.L-1, la concentration d’une eau oxygénée à 110 volumes. Quantité de matière de dioxygène n(O2) = V / Vm = 110 / 22,4 = 4,91 mol. H2O2(aq) =½O2(g) + H2O(l). D'après les coefficients stoechométriques de cette équation n(H2O2(aq)) = 2 n(O2) ==2*4,91 =9,82 mol dans 1 L. [H2O2(aq)] = 9,82 mol/L. Etude cinétique de la dismutation de l'eau oxygénée. On considère la réaction de dismutation de l’eau oxygénée en solution aqueuse : 2 H2O2(aq) --> 2 H2O(l) + O2(g). Les ions Fe3+ catalysent cette réaction. On considère un litre de solution de peroxyde d’hydrogène à la concentration initiale c0 égale à 2,0 mol.L-1. à l’instant t = 0, on introduit une faible quantité de catalyseur et on commence à mesurer le volume de dioxygène dégagé au cours du temps, VO2 , sous une pression totale constante P = 1,0 bar, à 298 K. On appelle x la quantité de matière de dioxygène dégagé à l’instant t. Donner l’expression de la vitesse de la réaction v(t). v(t) = 1 / V dx/dt avec V= 1 L : volume de la solution. Dans les conditions de la manipulation, la vitesse de la réaction est d’ordre 2 par rapport au peroxyde d’hydrogène. Exprimer v(t) en fonction de c0, x et k, constante de vitesse de la réaction à la température de l’expérience.  v(t) = k [H2O2aq]2 =k(c0-2x)2.  En reportant dans une équation différentielle issue des questions précédentes, vérifier que : 1/(c0-2x) -1/c0= 2kt. v(t) = dx/dt = k(c0-2x)2 ; dx / (c0-2x)2  = k dt. Intégrer : 1/(c0-2x) + cste= 2kt  ; à t = 0  : -1/ c0 = Cste. Expérimentalement, on obtient les résultats suivants, VO2 étant le volume de dioxygène dégagé au bout d’un temps t : t(min) 0 10 20 40 100 infini VO2(L) 0 7,0 10,8 15,0 19,5 Voo=24,4 VO2/(Voo-VO2) 0 0,40 0,80 1,60 4,0 xxxxx Montrer que la relation suivante est vérifiée : VO2 / (Voo-VO2) = 2c0kt. 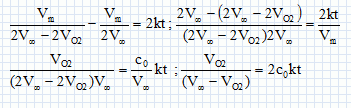 VO2 = x Vm ; Voo = ½c0 Vm ; avec Vm : volume molaire des gaz. 1/(c0-2x) -1/c0= 2kt s'écrit :

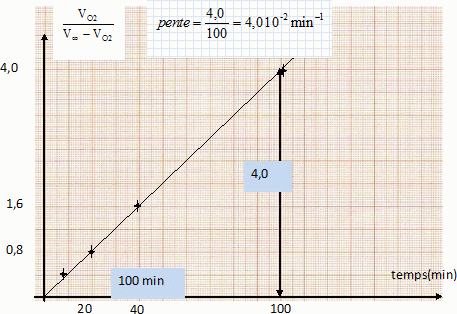
Vérifier graphiquement que la réaction est bien d'ordre 2 et en déduire la valeur de la constante de vitesse k. On trace le graphe VO2/(Voo-VO2) = f(t). On obtient une droite ( ce qui confirme l'ordre 2 par rapport à H2O2 ) de pente 0,04 = 2 c0 k. k = 0,04 / (2c0) =0,04 / (2*2) = 0,010 L mol-1 min-1.

menu