Un
puits canadien.
Un
puits canadien est un dispositif qui permet de tempérer, à moindre
coût, l'air de ventilation d'une maison. Il s'agit d'une simple
canalisation enterrée dans le sous-sol. On utilise le fait qu'à une
profondeur d'environ 2 m sous terre, la température est presque
constante toute l'année ( environ 13 °C sous nos latitudes ).
Un système de ventilation permet à l'air extérieur de pénétrer et de
circuler dans la canalisation : l'été, l'air ventilé dans la maison est
rafraichi, l'hiver, l'air est préchauffé.
Une fois installé, le seul coût provient de l'alimentation électrique
du système de ventilation. Ce coût est négligeable par rapport au gain
thermique.
|
|
Transfert
thermique et calorimétrie.
Etude
sans le puits canadien.
La période hivernale de chauffage dure 6 mois.
Les dimensions de la maison d'essai à toit plat sont :
longueur a = 5,00m ; largeur b = 3,00 m ; hauteur h = 2,30 m.
De l'intérieur, vers l'extérieur, les murs et le toit plat sont
constitués des matériaux suivants :
matériau
|
épaisseur
( cm)
|
conductivité
thermique ( W m-1 K-1)
|
plâtre
|
e1
=1,00
|
l1
=0,550
|
isolant
|
e2 =6,00 |
l2
=0,0450 |
béton
|
e3 =15,0 |
l3
=1,80 |
Les résistances
thermiques superficielles internes et externes des murs et du toit ont
pour valeur :
rsi =0,130 m2 K
W-1 ; rse
=0,0500 m2 K W-1.
Sur les murs il y a une porte ( 0,900 m x 2,10 m ) et deux fenètres (
1,00 m x 1,10 m ) dont l'une est à l'arrière de la maison ( non visible
sur le schéma ). Ces trois ouvertures sont constituées de double
vitrage dont la résistance thermique surfacique globale est rv
=0,170 m2
K W-1.
En période hivernale, la température intérieure est qi
= 20,0 °C et la température extérieure moyenne qe=3,00
°C.
On néglige les pertes thermiques intervenant par le sol.
Donner
l'expression littérale de la résistance thermique surfacique r1
des murs ou du toit plat. Calculer sa valeur.
r1 = e1 / l1 + e2
/ l2
+ e3 / l3 + rsi + rse
=0,01 / 0,55 +
0,06 / 0,045 +0,15 / 1,8 +0,130 + 0,05
r1
=1,6148 ~1,61 m2
K W-1.
Donner
l'expression littérale du flux surfacique f1, à
travers les murs ou le toit. Calculer sa valeur.
f1
= 1/ r1
(qi -qe ) = 1/ 1,6148 ( 20-3) =10,5276 ~10,5 W m-2.
Calculer
la valeur du flux thermique F1, à
travers les murs et le toit.
Surface du toit : ab = 3*5 = 15 m2 ;
surface des murs : (2a+2b) h -0,9*2,1 -2*1*1,1 =16*2,3 -4,09
=32,71 m2.
F1
=10,5276
*(32,71+15) =502,27 ~502 W.
Calculer
la valeur du flux thermique F2, à
travers les fenètres et la porte.
Surface de la porte et des fenètres : S = 4,09 m2.
F2
= 1/ rv
(qi -qe )S =1/0,170 *17*4,09 = 409 W.
Montrer
que la valeur de la puissance P des appareils de chauffage qui permet
de compenser les pertes thermiques est d'environ 910 W.
P = 409 +502 =911 W.
Déterminer,
en joules, la valeur de l'énergie E utilisée par les appareils de
chauffage en une journée.
Energie ( J) = puissance ( W) fois durée ( s)
E =911 *24*3600 =7,87 107 J.
|
Etude avec le puits canadien.
On met en marche le système de ventilation. l'air entre dans le puits
canadien à la température q1
= 3,00°C. En circulant dans la canalisation enterrée, il se réchauffe
et arrive dans la pièce à la température q2
= 11,0°C.
Pour obtenir une bonne aération, on veut renouveller l'air de la pièce
toutes les heures.
Montrer
que la masse d'air qui doit circuler dans la canalisation en une
journée est environ 1080 kg. ( masse volumique de l'air rair
= 1,30 kg m-3 )
Volume de la pièce V = abh = 5*3*2,3 =34,5 m3.
Volume d'air renouvellé en une journée : 34,5*24 =828 m3.
Masse d'air renouvellé par jour : m =828*1,3 =1076 ~1080 kg.
Montrer
que l'énergie thermique ( ou chaleur ) transférée à cette
masse
d'air dans la canalisation du puits canadien est environ 8,60 106 J.
Capacité thermique de l'air Cair = 1,00 103
J kg-1 K-1.
Energie =E'= m Cair
( q2- q1) = 1076 *1,00 103
*8 =8,61 106 J.
Le
puits canadien apporte t-il un gain énergétique significatif ? Justifier.
E' est environ égale à 0,1 E. Le puits canadien apporte environ 10 % de
l'énergie nécessaire au chauffage de la pièce.
Le kWh est facturé par le fournisseur d'électricité à un prix de 0,115
€. Justifier
l'affirmation suivante :
" le puits canadien permet d'économiser environ 50 € pour notre petite
maison d'essai, au cours d'une période de 6 mois ( 1 mois = 30 jours )
de chauffage".
Economie réalisée par jour : 8,61 106
/ 3,6 106 ~2,4 kWh.
Economie réalisée en 6 mois, soit 180 jours : 2,4*180 ~ 431 kWh
Economie : 431*0,115 ~ 50 €.
Mécanique
des fluides.
L'air de la petite maison d'esai doit être renouvellé toutes les heures.
Montrer
que le débit volumique qV de l'air circulant
dans la canalisation est égal à 9,60 10-3 m3
s-1.
Volume de la pièce V = abh = 5*3*2,3 =34,5 m3.
Volume d'air renouvellé en une heure : 34,5*1 =34,5 m3.
qV = 34,5 / 3600 =9,58 10-3
m3 s-1.
Le diamètre de la canalisation enterrée est d = 20,0 cm.
Montrer
que la vitesse de l'air dans la canalisation est égale à 0,305 m/s.
Section de la canalisation : S =pr2=
3,14 *0,102 =3,14 10-2 m2.
Vitesse = débit volumique / section = 9,58 10-3
/ 3,14
10-2= 0,305 m/s.
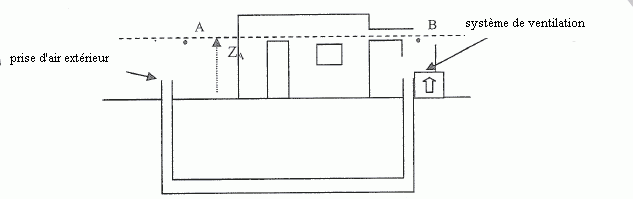
En faisant
les simplifications qui s'imposent, appliquer l'équation de Bernoulli
généralisée entre les points A et B de la maison d'essai ( zA=zB). En
déduire que la puissance Psys du système de
ventilation est légèrement inférieure à 1 W.
On donne pA =1,013 105 pa
; pB = 1,001pA.
relation de Bernoulli : ½(VB2-VA2)+
g(zB-zA)+( PB-PA)/rair = Psys / qmassique.
zA = zB : ½(VB2-VA2)+(
PB-PA)/rair = Psys
/ qmassique avec qmassique
= qvrair .
PB-PA=
(1,001-1)*1,013 105 = 101,3
pa.
En A l'air est quasiment immobile VA~
0 : ½VB2 +( PB-PA)/rair = Psys
/ qmassique.
Psys
= qmassique
(½VB2 +( PB-PA)/rair) =qvrair (½VB2 +( PB-PA)/rair) =9,58
10-3 *1,3 *(0,5 *0,3052
+101,3/1,3)= 0,97 W.
Déterminer
la valeur de l'énergie électrique Eélec
consommée en une journée par le système de ventilation. Conclure.
Eélec= Psys *24*3600 =0,97
*24*3600 =8,4 104 J.
Energie
apportée par le puits canadien en un jour : 8,61 106
J.
Energie consommée par la ventilation en un jour : 8,4 104
J.
Gain énergétique : 8,61 106
-8,4
104 =8,53 106
J.
Le coût
dû à la ventillation est négligeable par rapport au gain
thermique.
Chimie
organique et oxydoréduction.
Il y a plusieurs possibilités quand au choix du matériau constituant le
tuyau enterré dans lequel s'effectuent les échanges thermiques. Il est
courant d'utiliser des matières plastiques ou des tuyaux en fonte.
Comment
appelle t-on des matières plastiques de type PE ( polyéthylène) ou PVC
( polychlorure de vinyle )?
Polymères thermoplastiques.
Le PVC a pour formule chimique -(- CH2--CHCl- )
- n.
Donner
la formule chimique de la molécule à partir de laquelle il a été
synthétisé.
H2C=CHCl chlorure de vinyle.
Donner
le nom de l'indice n utilisé ci-dessus. A quoi correspond-t-il ?
Indice de polymérisation ou nombre moyen de motifs élémentaires (
monomère) constituant le polymère.
Les propriétés mécaniques et la conductivité thermique des tuyaux en
fonte sont bien meilleures que celles des tuyaux en plastique. Ils sont
par contre sujets à la corrosion du fer contenu dans la fonte. En
effet, le dioxygène contenu dans le sol, peut oxyder le métal fer. Afin
d'éviter ce phénomène, on peut, par exemple, recouvrir la fonte par du
zinc ( galvanisation ) : c'est le zinc qui est corrodé. L'intensité du
courant électrique résultant de ce phénomène de corrosion du zinc est
estimée à 15 mA.
On donne les potentiels standards d'oxydoréduction : E(Zn2+/Zn)
= -0,76 V ; E(Fe2+/Fe)
= -0,44 V ; E(O2
/ H2O) = 1,23 V.
Justifier
qu'une galvanisation du fer peut protéger celui-ci.
E(Zn2+/Zn)
<E(Fe2+/Fe)
: le zinc est un réducteur plus fort que le fer ; le zinc va donc
s'oxyder à la place du fer. Le fer est protégé tant qu'il y a du zinc.
Ecrire
les deux demi-équations d'oxydoréduction intervenant lors de la
corrosion du zinc, les deux couples mis en jeu étant Zn2+/Zn et O2 / H2O. En
déduire l'équation de la réaction de corrosion.
Oxydation du zinc : Zn = Zn2+ + 2e-.
Réduction du dioxygène : ½O2 + 2H+
+2e- = H2O.
Bilan : ½O2
+ 2H+ +Zn= H2O
+ Zn2+.
Déterminer
la quantité d'électricité mise en jeu en 20 ans. En déduire la quantité
de matière d'électrons échangés.
Q = I t avec I = 0,015 A et t = 20*365*24*3600 =6,31 108
s.
Q = 0,015 *6,31 108
=9,46 106 C.
n(e-) = Q / 96500 = 98,0 mol d'électrons.
Calculer
la quantité de matière, puis la masse de zinc consommée en 20 ans.
On donne M(Zn) = 65,4 g/mol.
Le zinc est bivalent : n(Zn) = ½n(e-)
=49,0 mol
masse de zinc consommée : n(Zn) M(Zn) =
49*65,4 =3,21 103 g = 3,21 kg.
|
|
