Diffraction
des ondes lumineuses.
On
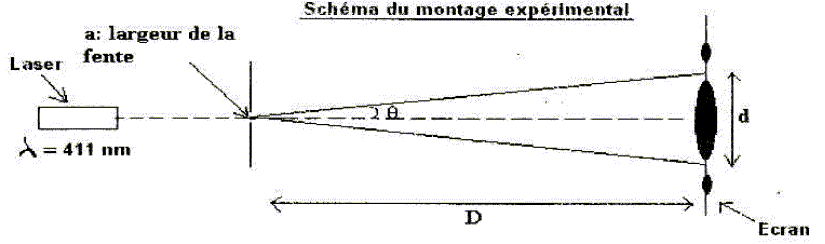
réalise une expérience de diffraction des ondes lumineuses à I'aide
d'un laser émettant une lumièrc monochromatique de 411 nm de longueur
d'onde, une fente de largeur a et un écran situé à
une distance D de la fente.
Donner
le domaine des longueur d'onde dans le vide associé aux radiations
visibles.
Les longueurs d'onde dans le vide des radiations visibles s'étendent de
400 nm à 800 nm.
Une
onde lumineuse est-elle une onde mécanique ? Justifier.
Une onde lumineuse est une onde électromagnétique, ce n'est
pas une onde mécanique.
Une onde électromagnétique peut se propager dans le vide ; une
onde mécanique nécessite un milieu de propagation.
Donner
la relation entre la longueur d'onde dans le vide, 1, la
célérité de la lumière dans le vide c et la période de l'onde T.
Préciser les unités.
l =
cT ; longueur d'onde en mètre, célérité en m s-1
et période T en seconde.
En
déduire la période T d'une onde électromagnétique de longueur d'onde l
=411 nm. c = 3,00 108 ms-1.
T = l / c =
411 10-9 / 3,00 108
=1,37 10-15 s.
On suppose qu'un faisceau parallèle de lumière de longueur d'onde l, traverse une
fente de largeur a.
Donner
la relation entre l'écart angulaire q du
laisceau diffracté, la longueurd 'onde l, et la
largeur de la fente a.
q = l / a. (1)
Sachant que pour les petits angles il est possible de faire
l'approximation suivante : tan q
~ q, l'angle
étant exprimé en radian,
donner
la relation entre q, la
distance entre la fente et l'écran D et la largeur de la tache centrale
de diffraction d.
tan q = ½d
/ D ; tan q
~ q
; q ~ d / (2D).
(2)
Etablir
la relation suivante : l / a = d/ / (2D).
En égalant (1)
et (2)
on trouve cette relation.
|
A.N : l = 411 nm ; D =
20 cm ; d = 1,0 mm.
a = 2 l D
/ d = 2*411 10-9 *0,20 / 1,0 10-3
=1,6 10-4 m = 0,16 mm.
A.N : l = 411 nm ; D =
20 cm ; d = 0,10 mm.
a = 2 l D / d = 2*411 10-9 *0,20 / 1,0 10-4 =1,6 10-3 m = 1,6 mm.
Un
spectrophotomètre comporte un dispositif qui permet de décomposer la
lumière blanche émise par la source lumineuse. Une fente fine permet
ensuite de sélectionner la radiation colorée désirée.
Expliquer
pourquoi il n'est pas possible d'utiliser une fente trop fine.
Une fente trop fine provoque un phénomène de diffraction, c'est à dire
un étalement de la lumière colorée.
|
Dosage
des ions nickel par spectrophotométrie.
On
dispose d'une solution de chlorure de nickel (II), de concentration
inconnue C. On veut déterminer par spectrophotométrie la concentration
C, en se plaçant à la longueur d'onde l = 411 nm. Une
série de 5 fioles jaugées de concentration différente CNi
en chlorure de nickel (II) sont analysées et leurs absorbances A sont
mesurées.
| concentation
( mol/L) |
0 |
3,0 10-2 |
6,0 10-2 |
9,0 10-2 |
1,2 10-1 |
1,5 10-1 |
| absorbance
A |
0 |
0,15 |
0,30 |
0,45 |
0,60 |
0,75 |
On dispose
d'une solution mère en chlorure de nickel (II) de concentration C0
= 0,50 mol/L. On désire péparer V1 = 50,0 mL de
solution fille à C1 = 3,0 10-2
mol/L.
Calculer le volume V0 de solution mère
nécessaire pour la préparation d'une telle solution.
Facteur de dilution : C0
/ C1
=0,50 / 3,0
10-2 =16,67.
V0 = V1 / F =50,0 /
16,67 =3,0 mL.
Choisir
parmi le matériel suivant celui qui est nécessaire à la préparation de
la solution fille.
éprouvette graduée de 10 mL ; pipette
graduée de 5,0 mL ; erlenmeyer de 50 mL ; pipette jaugée
de 10,0 mL ; becher de 50 mL ; fiole jaugée
de 50,0 mL.
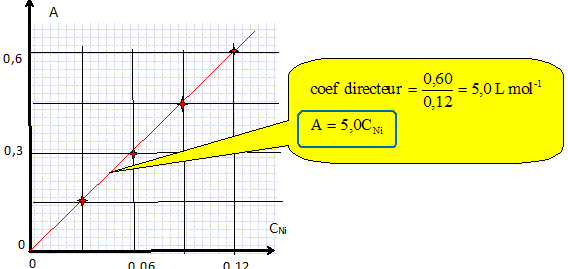
Tracer la
courbe représentant l'absorbance A en fonction de la
concentration.
Déterminer
la relation entre A et CNi.
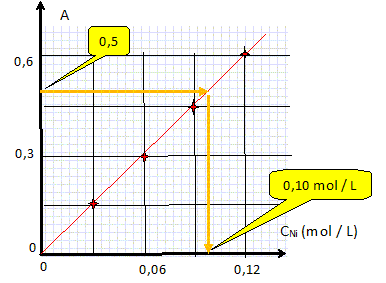
L'absorbance de la solution inconnue est A =0,50.
Calculer
la concentration de la solution inconnue.
C = A / 5,0 = 0,50 / 5,0 = 0,10 mol /L.
Vérifier
graphiquement la valeur de C. Justifier à l'aide du graphique.
|
Diagramme
d'énergie de l'atome d'hydrogène.
On
donne le diagramme énergétique de l'atome d'hydrogène.
Quelle
est l'énergie du niveau fondamental ? -13,6 eV.
Quelle est
l'énergie nécessaire pour ioniser l'atome d'hydrogène ?
+13,6 eV.
On
s'intéresse à la série de Balmer qui correspond à des transitions
électroniques d'un niveau supérieur vers le niveau n=2.
Représenter
sur le diagramme, les quatre premières transitions.
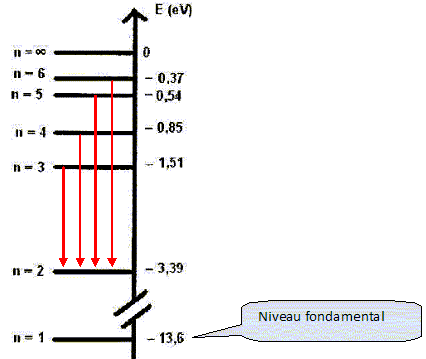
Calculer en nm la longueur d'onde
associée à la ransition électronique de l'atome d'hydrogène de n=6 vers
n=2.
Différence d'énergie E =E6-E2
=-0,37 -(-3,39) =3,02 eV.
3,02 *1,60 10-19 = 4,832 10-19
J.
E = h c / l ; l = hc /E = 6,62 10-34*3,00
108 / 4,832 10-19
=4,11 10-7 m = 411 nm.
On désire analyser l'absorbance de solutions de chlorure de nickel
(II).
Une
lampe à vapeur d'hydrogène est-elle utilisable comme source de lumière
pour cette expérience ?
Cette lampe est utilisable : la longueur d'onde correspondant au
maximum d'absorption de ces solutions est de 411 nm.
Cette lampe à vapeur d'hydrogène émet une radiation de longueur d'onde
411 nm.
Une lampe à vapeur d'hydrogène possède un nombre limité de radiations
visibles.
Est-il
possible de tracer le spectre d'absorption d'une solution de chlorure
de nickel (II), représenter ci-dessous, avec un spectrophotomètre
disposant uniquement d'une lampe à vapeur d'hydrogène comme source ?
Une telle source est-elle adaptée pour équiper un spectrophotomètre
?
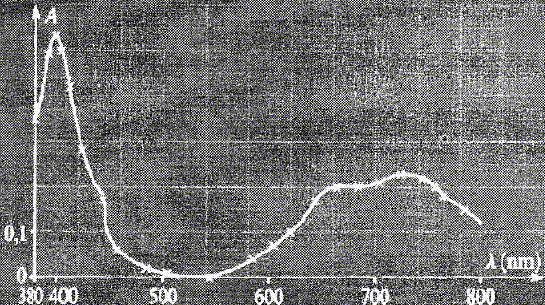
Pour déterminer le(s) maximum
d'absorption d'une solution colorée, on doit disposer d'une source de
lumière dont le spectre est continu de 400 nm à 800 nm.
La lampe à vapeur d'hydrogène, à elle seule, émettant un
spectre discontinu, ne suffit pas.
|
|




