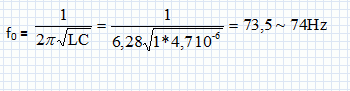Etude d'un circuit série en régime sinusoïdal ; étude d'une diode : bac STL 09/10

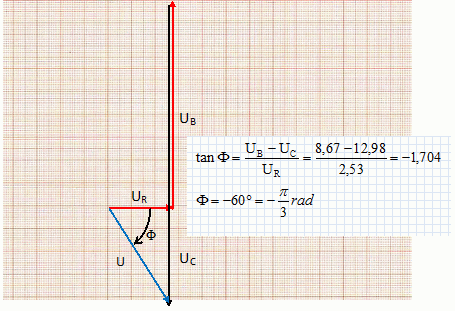
Un dipole est constitué de l'association en série d'un condensateur de capacité C = 4,7 µF, d'une bobine d'inductance L = 1,0 H et de résistance nulle, et d'un conducteur ohmique de résistance R = 110 W. Un générateur délivre une tension sinusoïdale u(t) de fréquence f = 60 Hz aux bornes de ce dipôle. On donne les valeurs efficaces des tensions aux bornes : - du condensateur UC =12,98 V - de la bobine UB =8,67 V - du conducteur ohmique UR =2,53 V. Calculer la valeur efficace I du courant circulant dans le circuit. La tension aux bornes d'un conducteur ohmique et l'intensité qui le traverse sont proportionnelles. UR = R I ; I = UR / R = 2,53 / 110 =0,023 A= 2,30 10-2 A. Calculer les impédances ZC du condensateur, ZB de la bobine et ZR du conducteur ohmique. ZC = UC / I  =12,98 / 0,023 =564,3 ~564 W. ZB = UB / I  =8,67 / 0,023 =376,96 ~377 W. ZR =R = 110 W. Etablir l'expression de la valeur instantannée i(t) de l'intensité du courant. i(t) = Imax  sin (2pft +J) avec Imax = 2½I. On prendra i(t)=0 si t = 0 : i(0) = Imax  sin (J)  =0 ; sin (J) =0 soit J = 0 ou p. i(t) =2½I  sin (2pft )  ; i(t) = 0,023 *1,414 sin (2*3,14*60 t ) ; i(t) = 0,0325 sin(377 t). En utilisant la construction de Fresnel relative aux tensions, déterminer graphiquement le déphasage F de la tension délivrée par le générateur par rapport à l'intensité. La tension u délivrée par le générateur a pour valeur efficace U = 5,0 V; la fréquence est toujours f = 60 Hz. 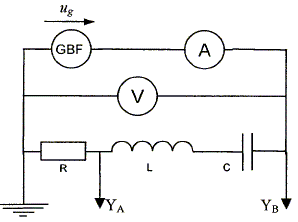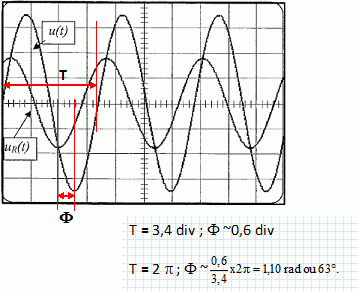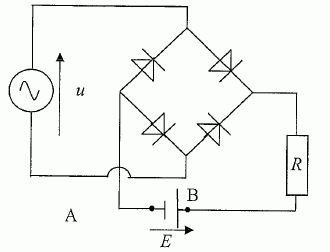Calculer la période et la pulsation de u(t). PériodeT = 1/f = 1/60 =0,01667 ~0,017 s ~ 17 ms. Pulsation w = 2 p f = 2*3,14*60 =377 ~3,8 102 rad/s. Donner l'expression de la valeur instantanée u(t). u(t) = 2½U sin ( wt+F) = 5*1,414 sin (3,8 102 t-60) u(t) = 7,1 sin (3,8 102 t-60). On veut visualiser sur un écran d'un oscilloscope les tensions u(t) et uR(t). Donner le schéma du montage en indiquant les branchements vers l'oscilloscope. Sur la voie B, on visualise la tension u(t) et sur la voie A, on visualise la tension uR(t). On obtient l'oscillogramme suivant. Lorsque les deux courbes sont croissantes, la première qui passe par un maximum est en avance sur l'autre. i(t) est en avance d'environ 63° par rapport à la tension. Le circuit est donc capacitif. 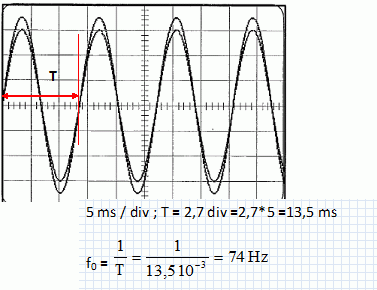La fréquence de la tension est réglée sur f0. On obtient l'oscillogramme suivant : En examinant la position relative des deux courbes, que peut-on dire des grandeurs u(t) et i(t) ? Les grandeurs u(t) et i(t) sont en phase. Préciser le nom du phénomène mis en évidence : déterminer la période et la fréquence f0. On observe le phénomène de résonance d'intensité. Retrouver f0 par le calcul. Calculer le facteur de qualité Q = Lw0/R et en déduire la valeur efficace de la tension aux bornes du condensateur. Q = 1*2*3,14*74 / 110 =4,2. Tension efficace aux bornes du condensateur : UC =Q U = 4,2*5 ~21 V. Le condensateur risque de claquer du fait de cette surtension à ses bornes. Etude d'une diode. On a mesuré la tension UD aux bornes d'une diode D et l'intensité I du courant qui la traverse. UD(V) -0,10 0,00 0,20 0,30 0,40 0,50 0,60 0,65 0,70 0,75 0,80 I(mA) 0,0 0,0 0,0 0,0 0,0 0,0 2,0 6,0 23 51 89 Représenter graphiquement I en fonction de UD et déterminer la tension de seuil Us de la diode. 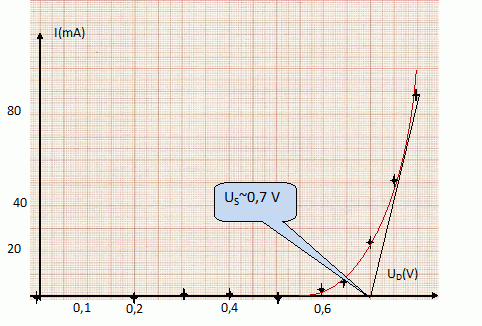La partie de la courbe limitée par les points P(0,75 V ; 51 mA) et Q (0,8 V ; 89 mA) est supposée linéaire. En déduire la résistance dynamique r de la diode. r =( 0,8-0,75) / (0,089-0,051)=1,316 ~1,3 W. Donner l'expression de la tension aux bornes de la diode en fonction de Us, r et I lorsque la diode est passante. Préciser l'expression simplifiée de cette tension si la diode est idéale. UD = Us+ rI ; pour une diode idéale UD = Us =0. La diode est supposée idéale. Dans le montage ci-dessous, les quatre diodes sont idéales. Préciser l'interêt de ce montage. Il s'agit d'un montage redresseur double alternance. A partir d'un courant alternatif, on obtient un cournt variable dont le sens ne change pas. Entre les points A et B du montage, on place une batterie de fem E = 12 V afin de la charger. La tension délivrée par le générateur a pour expression u(t) =24 sin(3,14 t), en volt ; la valeur de R est 10 W. Indiquer à quelle condition le courant i peut circuler dans R et dans la batterie. Représenter le schéma  simplifier du circuit, en tenant compte du fait que les diodes sont idéales. La tension aux bornes du pont de diodes est nulle. La batterie se comporte en récepteur. Additivité des tensions : u = E+Ri ; i = (u-E) / R u doit être supérieure à E. Calculer la valeur maximale du courant de charge. imax =(Umax-E) / R = (24-12) / 10 = 1,2 A.

menu