Convertisseur analogique numérique : bac STI électronique 2011.

Afin d’afficher la tension u2 (image de la température q), on insère dans le montage un échantillonneur bloqueur et un convertisseur analogique numérique (CAN) simple rampe 8 bits. Pour la suite du problème, on admettra que u2 = – 7,7 x 10-2 q. Le schéma synoptique de cette fonction est représenté : 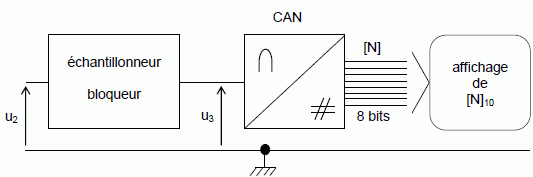Etude d’un échantillonneur bloqueur. Le schéma de principe est présenté : 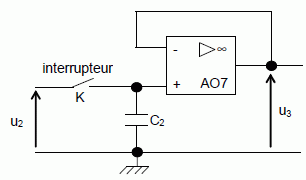Le montage comporte un interrupteur idéal K commandé périodiquement. Le CAN a une résistance d’entrée infinie. A t = 0 s, on ferme K. Exprimer u3 en fonction de u2 lorsque l’interrupteur est fermé. Le condensateur se charge ; quand la charge est terminée, la tension aux bornes du condensateur est égale à u2. L'AO 7 réalise un montage suiveur de tension : u3 = u2. A t = t1, on ouvre K. Comment évolue alors la tension u3 sachant que le CAN a une résistance d’entrée infinie ? Justifier la réponse. Le condensateur ne peut pas se décharger car la résistance d'entrée du CAN est infinie. La tension aux bornes du condensateur chargé reste constante, égale à u2. L'AO 7 réalise un montage suiveur de tension : u3 = u2. La tension u3 reste constante. Quel est le rôle d’un tel montage en amont d’un CAN ? Ce circuit, placé sur l'entrée analogique d'un CAN joue un double rôle : - Acquérir une valeur donnée de la tension  à l'entrée du CAN à un instant donné. - Maintenir cette valeur constante pendant toute la durée de la conversion. Etude du Convertisseur Analogique Numérique. On notera [N] la valeur binaire du mot numérique de sortie du CAN et [N]10 sa valeur décimale. La caractéristique de transfert du CAN, [N]10 = f(u3) se présente comme une succession de paliers s'appuyant sur une droite D comme le montre la figure : 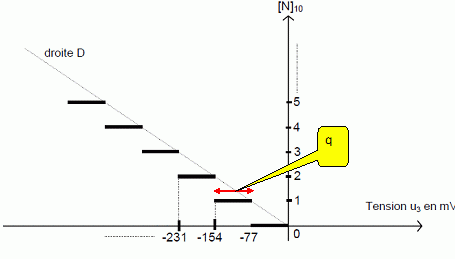. Quel est l’intérêt d’avoir un nombre de bits important ? La  résolution ou variation de la tension d'entrée donnant lieu à une variation d' une unité de la donnée numérique présente en sortie, est bien meilleure. Calculer le nombre de combinaisons possibles pour [N]. Il existe 28 combinaisons de sortie possibles soit : 28= 256. Déterminer [NMAX] et [NMAX]10. La première combinaison correspond à zéro ; la plus grande correspond à [NMAX] =255 " en décimal". 255 = 1*27 + 1*26 + 1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20 ; 55 sécrit : 1111 1111 en binaire et FF en hexadécimal. [NMAX]10 = [NMAX] *q = 255 *(-0,077) ~ -19,6 V. En pratique on ne peut pas dépasser la tension de saturation du CAN ( -Vsat  = -15 V) et dans ce cas [NMAX] =15 / 0,077=195 . Déterminer la valeur du quantum q. q =217-154 = 154 -77 = 77 mV. En déduire la valeur de la température maximale, notée qmax, que l’on peut afficher. qmax =-Vsat /( – 7,7 x 10-2 ) = -15 / ( – 7,7 x 10-2 )~ 195°C. Est-elle compatible avec les températures rencontrées lors de ce type de forage ? Oui : la température à une profondeur de 1000 m est 50°C et à 2500 m, 110°C.  Calculant la valeur de [N]10 aux diverses profondeurs. h = 1000 m ; q =50°C ; u2 = – 7,7 x 10-2 *50 = -3,85 V ; h = 2000 m ; q =90°C ; u2 = – 7,7 x 10-2 *90 = -6,93 V ; h = 2500 m ; q =1100°C ; u2 = – 7,7 x 10-2 *110 = -8,47 V.

menu