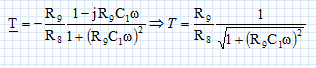|
Transmission optique, analyse harmonique, étude d'un filtre : bac STI électronique 2011. |
||||||||||||||||||||||
|
||||||||||||||||||||||
|
L’émetteur est réalisé autour d’une diode électroluminescente (D.E.L.) D2. Le détecteur est constitué d’une photodiode D3, comme le montre la figure n°7. 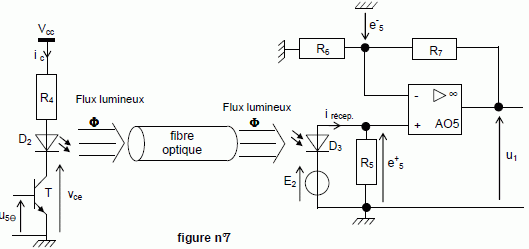 Le transistor bipolaire T fonctionne en commutation : - Lorsque u5q = 0 : le transistor T est bloqué, ic = 0 A - Lorsque u5q = +5 V : le transistor T est saturé, vce = 0 V La tension de seuil de la DEL D2 vaut : 2 V. On rappelle que Vcc = 15 V. L’amplificateur opérationnel AO5 fonctionne en régime linéaire. On néglige l’atténuation que subit l’intensité lumineuse dans la fibre optique. La transmission optique est du type « tout ou rien », on a alors : D2 bloquée (éteinte) --> F = 0 --> D3 bloquée --> i récep. = 0 A D2 passante (allumée) --> F = Fmax --> D3 passante -> i récep. = 250 µA (courant inverse de la photodiode) Citez l’un des avantages d’une transmission par voie optique. La transmission est rapide ( ~ 2 108 m/s) ; fréquence porteuse élevée ; faible atténuation linéique ( ) 0,2 dB /km ). On souhaite limiter l’intensité du courant dans la DEL D2 à la valeur 20 mA lorsqu'elle est passante. Calculer la valeur à donner à la résistance R4 pour assurer cette condition. VCE + VD2 seuil + R4icc = VCC. T est saturé, Vce = 0 V ; diode passante VD2 seuil = 2 V ; VCC = 15 V ; icc =0,020 A. R4 = (VCC-VD2 seuil )/ icc=(15-2)/0,020 =650 ohms. Donner le nom du montage réalisé avec AO5, R6 et R7. Amplificateur non inverseur.
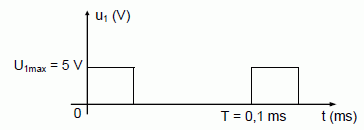 La tension u1, de fréquence F, admet la décomposition harmonique suivante, limitée aux 4 premiers termes : u1(t) = 1,25 + 2,25 sin (2p F t + j1) + 1,59 sin (4p F t + j2) + 0,75 sin (6p F t + j3) Que représente la constante de valeur 1,25 V dans l’expression de u1(t) ? L'amplitude du fondamental, valeur moyenne de u1, amplitude de la composante continue de u1. On souhaite mesurer cette grandeur avec un voltmètre numérique. Indiquer le réglage de l’appareil de mesure (AC, AC+DC ou DC). Voltmètre en position DC. Préciser la valeur de la fréquence du fondamental de la tension u1(t) ? T = 0,1 ms = 10-4 s ; f = 1/T = 104 Hz. Représenter l’allure du spectre en amplitude (valeur crête) de u1(t) - pour des fréquences f comprises entre 0 Hz et 30 kHz - en précisant les grandeurs, les unités et l’échelle. 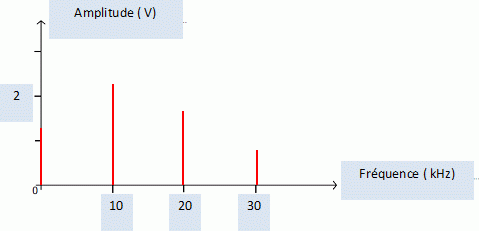
Etude du filtre. Le schéma fonctionnel du filtre est représenté : 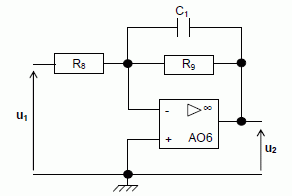 L’étude sera faite en régime sinusoïdal de pulsation w. On associe la grandeur complexe U1 à la tension u1 et la grandeur complexe U2 à la tension u2 de sortie du filtre. On définit la fonction de transfert du filtre : T = U2 /U1. Expression de la fonction de transfert complexe. Rappeler l’expression de l’admittance complexe YC d’un condensateur parfait de capacité C, puis celle de l’admittance complexe YR d’une résistance R. YC = j Cw ; YR = 1 /R. Déterminer l’expression de l’admittance complexe Y1 du dipôle équivalent à l’association de R9 et de C1 en fonction R9, C1 et w. Y1 = j C1w +1 /R9 = (j C1R9w +1) / R9. Montrer que la fonction de transfert du montage peut se mettre sous la forme : 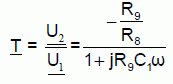 Z1 = 1 / Y1 =R9 / (j C1R9w +1). U1 = R8 i ; U2 + Z1 i = 0 ; U2 /U1 = - Z1 / R8 = -R9 /(R8(j C1R9w +1)). On souhaite avoir une amplification en tension en régime continu égale à – 4. Quelle valeur faut-il donner à R9, sachant que R8 = 10 kW ? En continu w=0 : T = -R9 /R8 ; R9 = -T R8 = 4*10 = 40 kW.
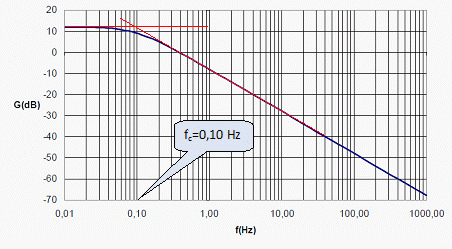
Sachant que l’expression de la pulsation de coupure à -3 dB est ωc =1/(R9C1), déterminer la valeur de la capacité du condensateur C1. C1 = 1/(R9ωc) avec ωc= 2pfc =6,28*0,1 = 0,628 rad/s. C1 =1/(4 104*0,628) ~4 10-5 F = 40 µF. Pour f = 1 kHz, que vaut le gain en tension du montage ? En déduire l’amplification en tension pour cette fréquence. G ~ -8 dB ; G = 20 log T ; log T = -8/20 = -0,4 ; T ~ 0,4. On rappelle que l’amplification en tension en régime continu vaut : – 4. Dans le cas où u1 = 1,25 V, calculer u2. u2 = -4 u1 = -4*1,25 = -5 V. Pour une fréquence de 10 kHz, l’amplification en tension vaut – 4 x10-5. Dans le cas où u1(t)= 2,25 sin (2.p.10000.t), calculer l’ordre de grandeur de l’amplitude de u2. 2,25 *|– 4 x10-5| = 9 10-5 V = 0,09 mV. On considèrera comme nulle une tension pour laquelle l’amplitude est inférieur à 1 mV. Déduire des questions précédentes l’expression de la tension u2 dans le cas où la tension u1 est : u1(t) = 1,25 + 2,25 sin (2p F t + j1) + 1,59 sin (4p F t + j2) + 0,75 sin (6p F t + j3). Les trois harmoniques ( de fréquences supérieures ou égales à 10 kHz) ont des amplitudes nulles. Donc u2 = -5 V. Quel est le rôle de ce montage ? A partir d'un signal périodique en forme de crénaux, on obtient une tension continue. |
||||||||||||||||||||||
|
|