Trajectoire et chute d'une flèche : bac S Polynésie 2011.

Les deux textes en italique s’inspirent d’extraits tirés du livre « Le monde a ses raisons » de Jean-Michel Courty et Edouard Kierlik. Trajectoire de la flèche. Sur les cibles de tir à l’arc se trouve un disque central de 10 cm de diamètre. À 70 m, l’archer le voit sous un angle de moins d’un dixième de degré, et doit ajuster la position de la corde et de ses mains au millimètre près […]. Dans quelle direction la flèche doit-elle partir pour parvenir au centre de la cible ? La résistance de l’air a ici relativement peu d’effet. La trajectoire de la flèche est à peu près balistique, c’est-à-dire de forme parabolique. On étudie dans le référentiel terrestre supposé galiléen le mouvement de la flèche assimilée à un point matériel de masse notée m. La situation est représentée sur la figure ci-dessous, sans souci d’échelle. Le champ de pesanteur g est parallèle à l'axe (Oz). On prendra g = 9,8 m.s-2. 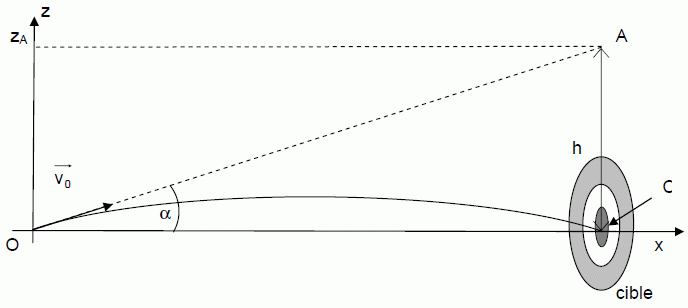Quelle force peut-on négliger d’après le texte introductif ? La résistance de l’air a ici relativement peu d’effet. On peut négliger les frottements sur les couches d'air. La poussée d’Archimède étant elle aussi ici négligeable, établir l’expression du vecteur accélération  de la flèche à partir du bilan des forces s’exerçant sur celle-ci. La flèche n'est soumise qu'à son poids. Ecrire la seconde loi de Newton dans le repère proposé.   On note alpha l’angle que fait le vecteur vitesse initiale v0 de la flèche avec l’axe horizontal (Ox). Les équations horaires paramétriques du mouvement du centre d’inertie sont : x(t) = v0.cosa.t (1) z(t) = -½gt2 + v0.sin a.t (2)  Montrer que l'équation de la trajectoire de la flèche est la suivante : 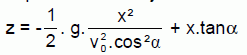 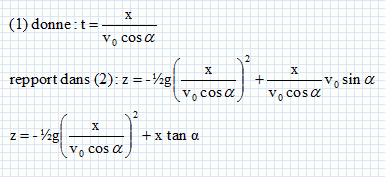Justifier la forme de la trajectoire indiquée à la fin du premier texte. La fonction z = f(x) est de la forme z = A x2 + Bx avec A et B des constantes : il s'agit de l'équation d'une parabole.   Chute de la flèche. Pour une vitesse initiale typique de 70 m/s (250 km/h), le vol dure environ une seconde. Au moment de toucher la cible, la flèche a chuté d’une certaine distance par rapport au point situé dans le prolongement de la direction de la vitesse initiale. Cette distance de chute, notée h sur la figure, est égale à la moitié du produit de l’accélération de la pesanteur par le carré de la durée du vol (gt²/2). Dans notre exemple, la « chute » est d’environ cinq mètres, d’où l’on déduit que la vitesse initiale de la flèche doit faire un angle de quatre degrés avec la droite joignant le tireur et le centre du blason. On note A le point situé dans le prolongement de la direction de la vitesse initiale. (voir figure). Durée du trajet de la flèche : Soit tC la date à laquelle la flèche atteint la cible. Cette date est égale à la durée du vol de la flèche. En utilisant l’équation horaire paramétrique (1), exprimer tC en fonction de v0, a et xC, abscisse du point C, centre de la cible. tC = xC / (v0.cos a) Vérifier à l’aide d’un calcul la cohérence des valeurs numériques données dans les deux textes encadrés précédents. alpha ~ 4 degrés ; v0 = 70 m/s ; xC = 70 m. tC = 70 / (70 cos 4) = 0,9975 ~ 1 s. tan a = h / xC = 5 / 70 =0,0714 ; alpha = 4,1 ~4 degrés. Les valeurs numériques proposées dans les deux textes sont cohérentes. Distance de chute  : Quelle hypothèse peut-on faire pour considérer que la flèche atteint le point A en gardant les mêmes conditions initiales de tir ? Préciser alors, en justifiant, la nature du mouvement de la flèche. Le mouvement de la flèche est rectiligne suivant OA avec une vitesse initiale v0. x(t) = v0.cosa.t (1) (2) s'écrit : z(t) = v0.sin a.t  . Le terme -½gt2  est négligé : le poids de la flèche est négligeable. La flèche n'étant soumise à aucune force,  ( solide pseudo-isolé ), le principe d'inertie indique que le mouvement de la flèche est rectiligne uniforme. On peut considérer que la durée du trajet hypothétique OA de la flèche et la durée tC du parcours parabolique OC sont identiques. Exprimer dans ces conditions la « distance de chute » h en fonction de v0, tC et a. h= v0.sin a.tC. En utilisant l’équation horaire paramétrique (2), retrouver alors que la « distance de chute » h, pour un tir réalisé dans les conditions réelles, est égale à « gt²/2 », comme indiqué dans le texte ci-dessus. zC =0 = -½gtC2 + v0.sin a.tC ;  v0.sin a.tC = ½gtC2  ; h = ½gtC2. Influence de la valeur de la vitesse initiale sur le tir. On suppose que l’archer vise toujours juste : l’angle a est constant et égal à 4°. On envisage une augmentation de la vitesse initiale v0, cette dernière restant cependant suffisamment faible pour permettre à la flèche de toucher la cible. Comment évoluent la durée du vol de la flèche et la « distance de chute » h. tC = xC / (v0.cos a) et xC et alpha sont constants : si v0 augmente, alors tC diminue. h = ½gtC2 et g est constant : or tC diminue, donc h diminue. Dans ces conditions, où la flèche va-t-elle frapper la cible ? h diminue : la flèche touche la cible un peu au dessus du centre de la cible.

menu