L'effet
Doppler fut présenté par Christian Doppler en 1842 pour les ondes
sonores puis
par Hippolyte Fizeau pour les ondes électromagnétiques en 1848. Il a
aujourd'hui de multiples applications.
Un
radar de contrôle routier est un instrument servant à mesurer la
vitesse des
véhicules circulant sur la voie publique à l'aide d'ondes radar. Le
radar émet
une onde continue qui est réfléchie par toute cible se trouvant dans la
direction pointée. Par effet Doppler, cette onde réfléchie possède une
fréquence légèrement différente de celle émise : plus grande fréquence
pour les
véhicules s'approchant du radar et plus petite pour ceux s'en éloignant.
En
mesurant la différence de fréquence entre
l’onde émise et celle réfléchie, on peut calculer la vitesse de la
«cible».
Mais
les radars Doppler sont utilisés dans d'autres domaines…
En météorologie,
le radar Doppler permet d'analyser la vitesse et le mouvement des
perturbations
et de fournir des prévisions de grêle, de pluies abondantes, de neige
ou de
tempêtes.
En imagerie
médicale, le radar Doppler permet d'étudier le mouvement des fluides
biologiques.
Une sonde émet des ondes ultrasonores et ce sont les globules rouges
qui font
office d'obstacles et les réfléchissent. L'analyse de la variation de
la
fréquence des ondes réfléchies reçues par cette même sonde permet ainsi
de
déterminer la vitesse du sang dans les vaisseaux.
D'après
le site : www.over-blog.com
Cet
exercice propose d'étudier le principe de l'effet Doppler sonore. Pour
simplifier cette approche, la réflexion de l'onde sur l'obstacle ne
sera pas
prise en compte.
Par
ailleurs, on rappelle que plus la fréquence est élevée, plus le son est
aigu.
|
Un
véhicule muni d'une sirène est immobile.
La
sirène retentit et émet un son de fréquence f
= 680 Hz. Le son émis à la date t = 0 se propage dans l'air à la vitesse c = 340 m.s-1 à partir de la
source S. On note λ la longueur
d'onde correspondante.
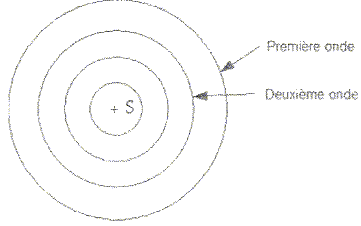
La
figure ci-dessous représente le
front d'onde à la date t = 4 T (T
étant la période temporelle de l'onde sonore.)
|
Répondre
par «vrai» ou «faux» aux sept affirmations suivantes en justifiant son choix.
Une onde sonore est
une onde transversale. Faux.
La propagation de la variation de pression a même direction que la direction de propagation de l'onde :onde longitudinale.
Une onde mécanique
se propage dans un milieu matériel avec transport de matière. Faux.
Une onde transporte de l'énergie ; elle ne transporte pas de matière.
La longueur d'onde
est indépendante du milieu de propagation. Faux.
La
longueur d'onde, comme la célérité, dépendent du milieu de propagation.
La fréquence, indépendante du milieu de propagation, est une
caractéristique d'une onde.
Un point M distant du point S d'une longueur égale à 51,0 m du milieu reproduit
le mouvement de la source S avec un retard Δt
=1,5 s. Faux.
Dt = 51,0 / 340 = 0,15 s.
Le front d'onde a parcouru d = 40.0 m à la date t =
3T. Faux.
T = 1 / f = 1/680 s.
d = 3v T = 3*340/680 = 1,5 m.
Deux points situés à la distance d’
= 55,0 m l'un de l'autre dans la même direction de propagation vibrent en
phase. Vrai.
Longueur d'onde l = v / f = 340 / 680 = 0,5 m.
d' / l = 55 / 0,5 = 110.
Des points distants d'un nombre entier de longueur d'onde vibrent en phase.
L'onde se réfléchit sur un obstacle situé à la
distance d" = 680 m de la
source. L'écho de l'onde revient à la source 2,0 s après l'émission du signal. Faux.
L'onde
incidente parcourt la distance d" en d"/v =680/340 =2 s. L'onde
réfléchie parcourt la distance d" en 2s et revient à la source 4 s
après l'émission.
Le véhicule se déplace maintenant vers la droite à la
vitesse v inférieure à c.
La figure
donnée ci-après représente le front de l'onde sonore à la date t = 4 T.
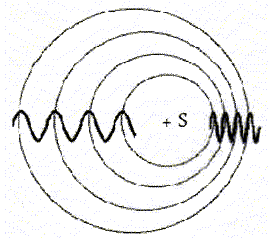
Donner la définition d'un milieu dispersif. L'air est-il
un milieu dispersif pour les ondes sonores ?
Dans
un milieu dispersif, la célérité de l'onde dépend de la fréquence.
L'air n'est pas un milieu dispersif pour les ondes sonores.
Le véhicule se rapproche d'un observateur immobile.
Pendant l'intervalle de temps T, le son parcourt la distance l.
Pendant ce temps, le véhicule parcourt la distance d
= v. T.
La longueur d'onde λ'
perçue par l'observateur à droite de la source S a donc l'expression suivante : l' = l - vT (1)
Rappeler la relation générale liant la vitesse
de propagation, la longueur d'onde et la fréquence.
La longueur d'onde l (m) est égale à la célérité c (m/s ) divisée par la fréquence (Hz). l = c / f.
En déduire que la relation (1) permet d'écrire f ' = f c / (c-v) (f ’ étant la fréquence sonore perçue par l'observateur).
l' = c / f '= l - vT = l - v/ f.
Or l = c / f d'où l' = c / f '= (c-v) / f ; f ' = c f / (c-v).
Le son
perçu est-il plus grave ou plus aigu que le son d'origine ? Justifier.
c / (c-v) est supérieur à 1 : donc f ' est supérieur à f ; si la fréquence augmente, le son perçu est plus aigu.
|
|
Dans un deuxième temps, le véhicule s'éloigne de
l'observateur à la même vitesse v.
Donner, sans démonstration, les expressions de
la nouvelle longueur d'onde λ"
et de la nouvelle fréquence f "
perçues par l'observateur en fonction de f,
v et c.
Le sens de la vitesse du véhicule change : il suffit de remplacer dans les expressions précédentes v par -v.
l" = l + vT
f " = c f / (c+v).
Le son perçu est-il plus grave ou plus aigu que
le son d'origine ? Justifier.
c / (c+v) est inférieur à 1 : donc f" est inférieur à f ; si la fréquence diminue, le son perçu est plus grave.
Exprimer, puis estimer en km.h-1, en
arrondissant les valeurs à des nombres entiers, la vitesse du véhicule qui se
rapproche de l'observateur sachant que ce dernier perçoit alors un son de
fréquence f ' = 716 Hz.
f ' = c f / (c-v).
f' (c-v) = c f ; c-v = c f / f ' ; v = c(1-f / f ') =340(1-680/716) =17,095 m/s.
17,095*3,6 =61,5 ~ 62 km / h.
|

