Régimes transitoires : dipôles  RLC.

Exercice 1. A l'instant t =0, le condensateur est déchargé. On suppose que RC = L/R. 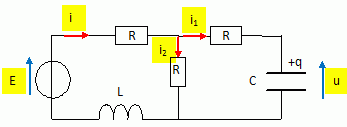Expression de l'intensité u(t). u +Ri1 = Ri2 et i1 = dq/dt = Cdu/dt = Cu'. i2 = i1+ u / R = Cu'+u / R . Loi des noeuds pour l'intensité : i = i1 + i2 ; i = Cu' +Cu'+u / R  = 2Cu' + u/R De plus : E = Ri + Ri2 + Ldi/dt ; E = 2CRu' + u + u + RCu' + 2LCu" +L/Ru'. E = 4RC u'+2u +2LCu". u" +2/(RC)u'+u/(LC) = E / (2LC). (1) Solution particulière de (1) : (en régime permanent la bobine se comporte comme un interrupteur fermé ) u(infini) = ½E. Solution générale de  : u" +2/(RC)u'+u/(LC) =0. Equation caractéristique associée : r2 +2/(RC) r +1/(LC)  = 0. D =4/(RC)2-4 /(LC) = 4 [LC-(RC)2] / (R2C3L) =0 car R2C = L. r =-1/(RC) et  u(t) = A exp(r t) (A+Bt). Solution générale de (1) : u(t) =  exp(r t) (A+Bt)+½E. Détermination des constantes A et B : u(0) = 0 = A+½E soit A = -½E ( continuité de la charge portée par le condensateur ). i(0) = 0 : continuité de l'énergie stockée par la bobine ; u(0) +Ri1 (0)= R ( -i1 (0) )  ; i1 (0) = -u(0) / (2R) = 0 i1 = Cu' = C exp(r t)[r  (A+Bt) +B] ; i1(0)=0 = C ( r A+B) ; B = -rA = -E / (2RC). u(t) = ½E exp(r t) (-1-1/(RC)t)+½E. u(t) = -½E exp(r t) (1+1/(RC)t)+½E. 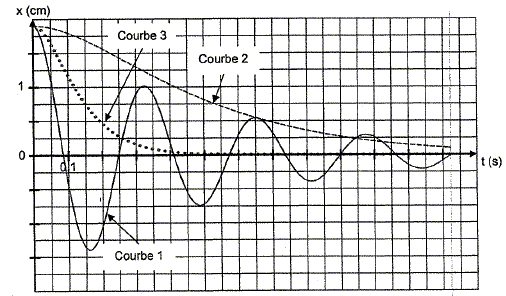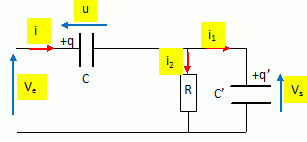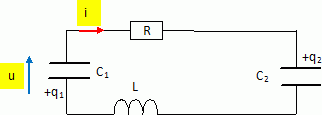Expression de l'intensité i(t). u' = -½E exp(r t) [r(1+1/(RC)t)+1(RC) u' = -½E exp(r t) ( t/(RC). i(t) = 2Cu' + u/R. i(t) =  E/R exp(r t) [t / (2RC) -0,5] +0,5 E / R.   Exercice 2. Initialement le condensateur de capacité C2 est déchargé et le condensateur de capacité C1 porte la charge q0. De plus C= C1=C2. Expressions de u(t) et i(t). On pose RC = t ; w02 = 2/(LC) et 2l = R/L. Additivité des tensions : u = Ri +q2/C2 +Ldi/dt. Dériver par rapport au temps : u' = R i' +1 / C2 dq2/dt + L i" Or  i = dq2/dt ;  u = -q1 / C1 ; i = dq1/dt. -1 / C1 dq1/dt = R i' +1 / C2 i + L i" -1/Ci = R i' +1 / C i + L i" ; i" +R/L i' +2/(LC) = 0 i" + 2l i' +w02i = 0. L'équation caractéristique associée  s'écrit : r2 + 2l r +w02=0 ; discriminant réduit D =4l2-4w02 Si D>0 , régime apériodique ( courbe 3). Si D<1 , régime pseudopériodique ( courbe 1). Si D= 0, régime critique( courbe 2). 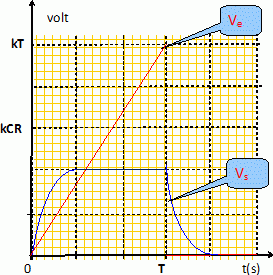Exercice 3. Les condensateurs sont initialement déchargés. Equation différentielle vérifiée par Vs(t). Vs =Ri2 ; i2 = Vs / R ;  Vs = q' / C' avec i1 =dq' /dt ; dVs/dt =  1/C' i1 soit i1 =  C' dVs/ dt. Additivité des tensions : Ve = u + Vs ; u = Ve-Vs. i = dq/dt = Cdu/dt = CdVe/dt -CdVs/dt. Loi de noeuds concernant les intensités : i = i1 + i2. CdVe/dt -CdVs/dt = C' dVs/ dt + Vs / R. (C+C') dVs/dt + Vs / R = CdVe/dt. R(C+C') dVs/dt + Vs = CR dVe/dt. Ve (t) = kt pour t compris entre 0 et  T ; Ve (t) =0  pour t négatif et pour t >T. ( k est une constante). On suppose T >> R(C+C'), les condensateurs ont le temps de se charger complètement. Courbe Vs(t)  : on pose t = R(C+C'). t compris entre 0 et  T : dVe/dt = k et R(C+C') dVs/dt + Vs  =kRC  ; dVs/dt + Vs / t  =kC / C+C') (2) pour t négatif et pour t >T : dVe/dt = 0 et dVs/dt + Vs / t  =0. (1) Solution générale de (2) : solution générale de (1) + solution particulière de (2). Vs = A exp(-t/t) + kCR. Vs (0-) = 0 = A +kCR ; le condensateur C' n'est pas encore chargé. Vs = kCR(1- exp(-t/t)). Solution générale de (1) : Vs = B exp(-(t-T)/t). Vs (T) = Vs (infini)=kCR ( continuité de la charge).   = Vs(T) = B. Vs = kCR exp(-(t-T)/t). Exercice 4. Charge initiale du condensateur : q0. A la fermeture du circuit, on observe une décharge oscillante peu amortie. Expression de la charge q(t) . i = -dq/dt ;di/dt = - d2q/dt2. u = Ri1 soit i1 = u/R avec u = q/C d'où i1 = q / (RC) et di1/dt = 1/(RC) dq/dt. u = Ldi2/dt ; di2/dt  = u/L = q / (CL). Loi des noeuds : i = i1+i2 soit di/dt = di1/dt + di2/dt. - d2q/dt2 = 1/(RC) dq/dt + q / (CL). d2q/dt2 + 1/(RC) dq/dt + q / (CL)=0 On pose w02 = 1/(LC)  ; t = RC et 2l = 1/(RC). d2q/dt2 +2l dq/dt +  w02q = 0 L'équation caractéristique associée  s'écrit : r2 + 2l r +w02=0 ; discriminant réduit D =4l2-4w02. L'amortissement étant faible, le discriminant est positif. q(t) = A exp(-t/t) cos (w0t) + B. q(0) = q0 =A + B. Intensité  : i(t) = -dq/dt = A exp(-t/t) [ -1/t cos (w0t) -sin (w0t) ]. i2(0) = 0 : continuité de l'énergie dans la bobine. i(0) = i1(0) = u/R = q0/(RC) = A/t ; d'où A = q0 ; par suite B = 0. q(t) = q0 exp(-t/t) cos (w0t).

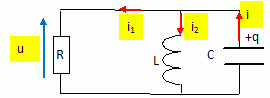
Exercice 5.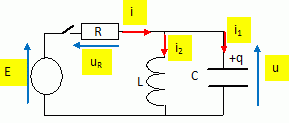 Initialement  (t = 0, fermeture de l'interrupteur)  i2 = 0 et le condensateur est déchargé. Intensité et tension à t = 0+. Continuité de l'énergie stockée par la bobine : i2(0) = i2 (0+) = 0 ; Continuité de la charge du condensateur : q(0) = q(0+) = 0 ; par suite u(0) = u(0+) = 0. Le condensateur se comporte comme un interrupteur fermé et court-circuite la bobine. Loi des noeuds : i = i1 + i2 ; i(0+ ) =i1(0+) + i2 (0+) =i1(0+) = E / R. uR(0+) = Ri(0+ ) = E. Intensité et tension en régime permanent. i1(t --> oo) = constante ; tension aux bornes de la bobine : u(t --> oo)= Ldi1(t --> oo) / dt = 0. La bobine court-circuite le condensateur : i1(t --> oo) i(t --> oo ) =i1(t --> oo) + i2 (t --> oo) =i2(t --> oo) = E / R. uR(t --> oo) = Ri(t --> oo ) = E. Equation différentielle vérifiée par u(t). Loi des noeuds : i = i1 + i2 ;d i /dt= di1/dt + di2 /dt. u = Ldi2 /dt ; u = q/C avec i1 =dq/dt = Cdu/dt ; di1/dt = C d2u/dt2. i = uR/R = (E-u) / R ; di/dt = -1/R du /dt Par suite : -1/R du /dt = C d2u/dt2 +u / L. d2u/dt2 +1/(RC) du /dt + 1/(LC) u = 0. A.N : E = 10 V ; R = 5 kW ; L = 1 H ; C= 1 µF. 1/(RC) = 200 ; 1/(LC) = 106. u" + 200 u' +106u = 0 Expression de u(t) : Equation caractéristique associée : r2 +200 r + 106 = 0 ; discriminant D = 2002-4 106 <0. Solution du type u(t) = A exp(-b/(2a) t sin ( (-D)½ / (2a)t+B) avec A et B des constantes. u(t) = A exp(-100t) sin (995t + B). Détermination des constantes : u(0) = 0 = A sin B, A n'est pas nul, donc B = 0. i1(t) = Cdu/dt = A C exp(-100t) ( -100 sin (995 t) +995 cos ( 995t)). i1(0) = E / R= 995 A C ; A = E / (995 RC) =2,0 V. u(t) = 2 exp(-100t) sin (995t ). Ouverture de l'interrupteur en régime permanent. Cet instant de l'ouverture est choisie comme nouvelle origine des dates. Il y a un échange permanent d'énergie entre bobine est condensateur. On observe des oscillations périodiques sinusoïdales non amorties. u = Ldi/dt  = q / C avec i = -dq/dt =-C du/dt ; di/dt = d2u/dt2. par suite u  = -LC d2u/dt2 ; u" + 1/(LC)u = 0. Solution du type : u = A sin (1/(LC)½t +B) = A sin(1000t +B). u(0) = 0 = A sin B soit B = 0. i(0) = E /R  = 10 / 5000 =2 10-3  ; i(t) = -C du/dt =-1000A C cos(1000t) 2 10-3 = -1000 A C = -10-3 A ;  A = -2. u(t) = -2 sin (1000 t).

menu