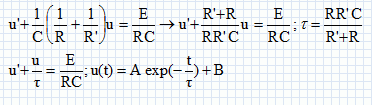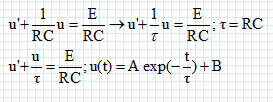Exercice 1.
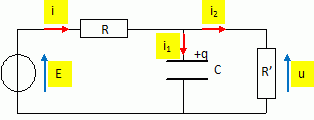
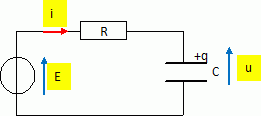
Un condensateur de capacité C possède une résistance de fuite R'. Il
est associé en série avec un conducteur ohmique de résistance R et un
générateur de tension idéal, de fem E.
A l'instant t =0, le condensateur est déchargé.
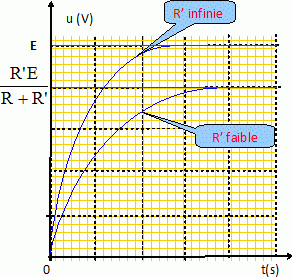
Expression
de la tension u(t) aux bornes du condensateur.
Loi des noeuds pour
l'intensité : i = i1 + i2.
u = R'i2 soit i2 = u / R' ; i1 = dq/dt
= Cdu/dt = C u'.
Additivité des tensions : E = Ri + u soit i = (E-u) / R.
Par suite : (E-u) / R = C u' +
u/R' ;
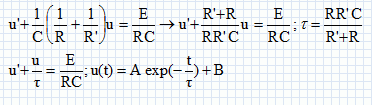
Détermination des
constantes A et B :
u(0) = 0 = A+B soit A = -B ( continuité de la charge portée par le
condensateur )
Au bout d'un temps très long, le condensateur chargé se comporte comme
un interrupteur ouvert : i = i2 ; E = Ri+R'i ; i =E / (R+R')
u( infini) = R'i = R'E / (R+R') d'où B = R'E / (R+R')
u(t) =
R'E
/ (R+R') ( 1-exp(-t/t) ).
|
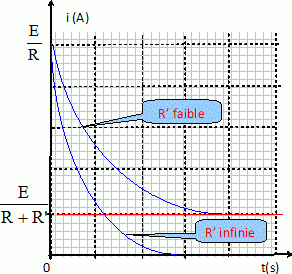
Expression
de la tension i(t) .
i = (E-u) / R.
i(t=0+) = E / R ; i (t infini) = E / (R+R').
|
Exercice 2.
E = 10 V ; la tension initiale aux bornes du condensateur vaut u(0) = u0=
2 V.
A t = 10 ms : u =6 V et l'intensité i vaut i = 1 mA.
Calculs
de R et C.
Additivité
des tensions : E = Ri + u avec i = dq/dt = Cdu/dt = Cu'.
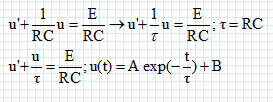
u(0) = u0 = A+B ; u(t infini) = E = B. Par suite A = (u0-E).
u(t) = (u0-E) exp(-t / t)
+E ; u(t) = -8 exp(-t / t)
+ 10.
1ère
relation entre R et C.
u(0,01) = -8 exp(-0,01 / (RC)) +10 = 6 ; 0,5 = exp(-0,01 / (RC)) ; ln
0,5 = -0,01 / (RC) ; RC = 1,4426 10-2 s.
2ème relation
entre R et C.
i(t) = Cu' = 8 / R exp(-t / t)
; i(0,01) = 10-3 = 8 / R exp(-0,01 / (RC)) = 8 / R *0,5 ; R = 4 103 ohms.
C = 1,4426 10-2 / 4000 = 3,6 10-6 F = 3,6 µF.
Exercice 3.
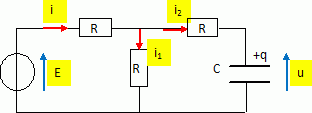
Le condensateur est initialement déchargé.
Expression
de u(t).
Additivité des tensions : 0,5E = 1,5Ri + u avec i = dq/dt = Cdu/dt =
Cu'.
0,5 E = 1,5 RC u' + u ; u' + u / (1,5 RC) = E / (3RC). On pose t = 1,5 RC.
u(t) = A exp(-t/ t) +B.
Détermination des
constantes A et B :
u(0) = 0 = A+B soit A = -B ( continuité de la charge portée par le
condensateur )
Au bout d'un temps très long, le condensateur chargé se comporte comme
un interrupteur ouvert : u (infini) = 0,5 E = B ; par suite A = -0,5 E.
u(t) = 0,5 E ( 1-exp(-t/ t) ).
|
Exercice 4.
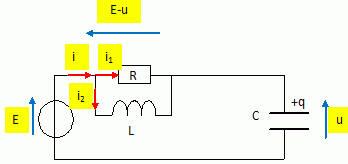
C = 1µF; L= 1 mH ; R = 10 ohms ;
Expression
de la tension u(t) aux bornes du condensateur.
A t = 0, le condensateur est déchargé ; la conservation de la charge impose u(0) = 0.
La continuité de l'énergie stockée par la bobine conduit à i2(0) = 0 ; alors i1 (0)= i (0) = E/R.
Au bout d'un temps suffisamment long
( régime permanent) , la tension aux bornes de la bobine idéale est
nulle ( la bobine se comporte en interrupteur fermé et court-circuite
R). La tension aux bornes du condensateur est alors égale à E.
Loi des noeuds pour les intensités : i = i1 + i2 ; di/dt = di1/dt +di2/dt.
i1 = (E-u)/ R ; di1/dt = -1/R du/dt = -u'/R.
tension aux bornes de la bobine : Ldi2/dt = E-u ; di2/dt =( E-u) / L.
i = dq/dt = Cdu/dt = Cu' ; di/dt = Cd2u/dt2 = Cu".
par suite : Cu" = -u'/R+( E-u) / L.
u" +u' / (RC) + u / (LC) = E/(LC) (1)
Solution particulière de (1) : u = E.
RC = 10*10-6 = 10-5 s = 10 µs ; LC = 10-3*10-6 = 10-9.
Solution générale de : u" +105 u' +109 u = 0.
Equation caractéristique associée : r2 +105 r +109 = 0.
D =1010-4 109 = 6 109 ; D½ =7,75 104.
r1 =½( -105 + 7,75 104)= -1,13 104 ; r2 =½( -105 - 7,75 104)= -8,88 104.
u(t) = A exp(r1 t) + B exp(r2 t)
Solution générale de (1) : u(t) = A exp(r1 t) + B exp(r2 t)+E.
Détermination des
constantes A et B :
u(0) = 0 = A+B+E ; A = -E-B.
Intensité i = Cu' = 10-6[ r1A exp(r1 t) +Br2exp(r2 t)]
i(0) =E/R = 10-6[ r1A +B r2] ; 0,1 E = 10-6[ -1,13 104 A -8,88 104 B ]
0,1 E = -1,13 10-2 A -8,88 10-2 B ;
0,1 E = -1,13 10-2 (-E-B) -8,88 10-2 B ;
0,1 E -1,13 10-2 E= (1,13 10-2 -8,88 10-2) B ; B = -1,145 E ; A = 0,145 E.
u(t) = E[ 1 +0,145 exp( -1,13 104t) -1,145 exp( -8,88 104t) ].
A.N : calcul de u(10-5).
u(10-5) = E[1 +0,145 exp( -0,113) -1,145 exp( -0,888 ) ] =0,66 E.
|
|
|
|