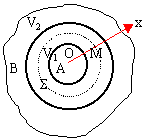
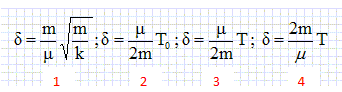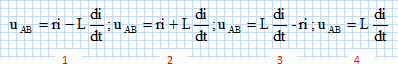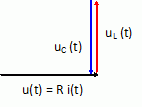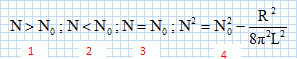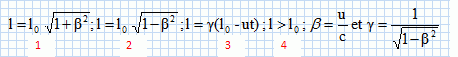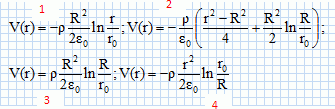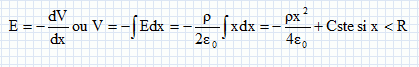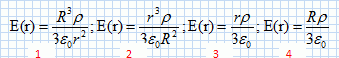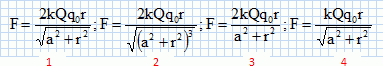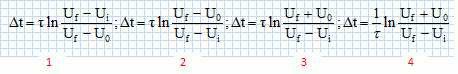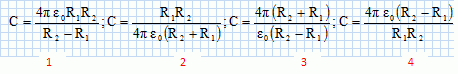Oscillateur
mécanique faiblement amorti.
L'oscillateur est constitué d'un solide de masse m et d'un
ressort de raideur k.
x(t) = A exp(-µ / (2m) t ) cos (Wt+
j).
A et f sont des constantes ;
µ : coefficient de frottement ; W
: pseudopulsation du mouvement ; w0
: pulsation propre de l'oscillateur.
Quelle est la
pseudopulsation du mouvement ?
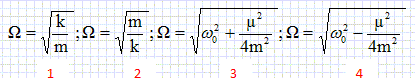
Analyse :
Les
vecteurs sont écrits en gras et en bleu.
On note f = -m v la force de frottement fluide, où m est une constante et v
le vecteur vitesse de la masse en translation.
Ecrire la seconde loi de newton sur
un axe horizontal, orienté de gauche à droite ; l'origine de l'axe est
la position d'équilibre stable du système masse ressort.
mg-kx-mv= m d²x/dt² ; m d²x/dt² +mv + k x=0 avec v = dx/dt =
x' ; m d²x/dt² +mx' + k x=0 (1)
(1 ) peut s'écrire : d²x/dt² +m/ m x' + k/ m x=0.
or w20 = k/m et on pose 2l= m /m ; d'où : d²x/dt² +2l x' + w20 x=0
(2)
équation caractéristique r2+2l r + w20
=0 ; discriminant D = 4l2-4w20.
On pose W2 =w20
-l2; W = [w20 -l2]½
= [w20 -µ2/ (4 m2)]½ .
La pseudopériode est la proposition n° 4.
|
Décrément
logarithmique de
l'oscillateur précédent :
Quel
est le décrément logarithmique ?
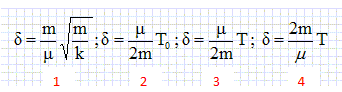
T : pseudopériode ; T0
: période propre.
Analyse :
On
appelle décrément logarithmique la grandeur sans dimension d = ln (x(t) / x(t+T)], où T désigne la
pseudo-période.
x(t)
= A exp(-µ / (2m) t ) cos (Wt+
j).
x(t+T) = A exp(-µ / (2m) (t+T) ) cos (W(t+T)+
j)=A exp(-µ / (2m)
(t+T) ) cos (Wt+ j).
x(t) / x(t+T) = exp(-µ / (2m) t ) / exp(-µ / (2m) (t+T) ) = exp(µ / (2m) T) .
d =µ
/ (2m) T. (
proposition n°3 )
|
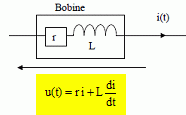
Bobine
inductive parcourue par un courant variable i de sa borne A vers
sa borne B:
Quel est
la tension à ses borens ( convention récepteur ) ?
r : résistance de la bobine ; L :
inductance de la bobine.
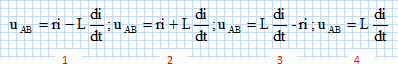
 (
proposition n°2 )
(
proposition n°2 )
Dipôle
RLC alimenté par une tension u(t) = Um sin (wt+j) :
A la
résonance d'intensité, la tension u(t) est :
en phase avec uc(t) ; en retard de phase par rapport à i(t)
; en quadrature avance par rapport à
uc(t)
; en quadrature retard par rapport à uc(t).
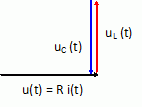
Oscillations
entretenues d'un oscillateur RLC :
On utilise un montage à résistance négative. Les oscillations sont
quasi-sinusoïdales de fréquence N. ( N0 : fréquence propre
de l'oscillateur ).
Que
vaut N ?
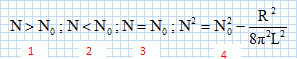
Le dispositif à résistance négative
compense à chaque instant l'énergie perdue par effet Joule dans le
dipôle. ( proposition n°3 )
Choc
élastique :
Deux particules sont animées de vitesses initiales v1 et v2,
avec v1 différent de v2. Après le choc les
vitesses sont v'1 et v'2, le coefficient
de restitution est e =(v'2- v'1 ) / ( v2-v1 ).
Le choc est
parfaitement élastique si :
e=0 ; e >0 ; e = 1 ; e est compris entre 0 et 1, bornes
comprises.
Dans un choc élastique,
l'énergie cinétique se conserve : e = 1.
Transformation
de Lorentz :
On
considère deux référentiels R et R' en translation rectiligne uniforme
l'un par rapport à l'autre, à la vitesse u parallèle à l'axe Ox. Les
orignes O et O' coïncident à l'origine des temps.
Une tige rigide, au repos, de longueur l0 dans le
référentiel R' est disposée parallèlement à l'axe Ox.
Quelle est la
longueur de la tige dans le référentiel R ?
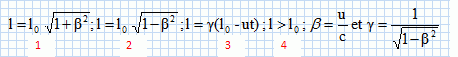
( proposition n°3 ).
Potentiel
électrostatique.
Soit une distribution de charges S
répartie avec une charge volumique r
uniforme, dans un fil cylindrique de rayon R.
En coordonnées cylindriques, en un poitnt M situé à la distance r de
l'axe de ce fil ( r >> R et r << L, longueur du fil),
l'expression
du potentiel électrostatique est :
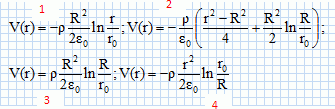
Analyse :
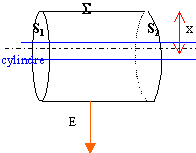
flux de
E à travers S.
En tout point de la surface latérale S, par raison de symètrie, le champ est
radial et a même module. Le flux de ce vecteur à travers la surface
latérale de longueur h est E 2pxh.
En tout point de S1 ou S2 le vecteur E est
normale au vecteur surface : le flux de E est nul à travers les 2 bases.
charge intérieure au cylindre S de
rayon x :
x < R : Q=px²hr
; x >= R : Q=pR²hr.
th de Gauss : E 2pxh = Q/e0.
x < R : E= xr / (2e0)
; x >= R : E= R²r / (2e0x)
potentiel électrique
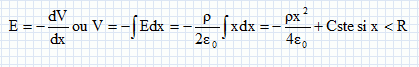
si x > R : V = -R²r / (2e0) ln(x) + Cte. (
proposition n°1 ).
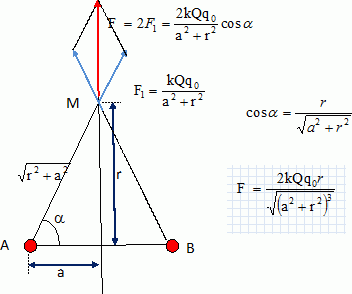
Champ électrique créé par une sphère.
La sphère, de rayon R, est uniformément chargée de densité volumique r.
L'expression
du champ électrostatique en un point M, extérieur à la sphère, est :
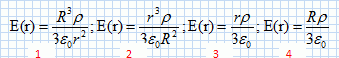
Analyse :
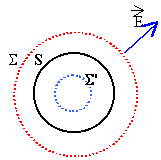 Par raison de symétrie, le champ est radial.
Par raison de symétrie, le champ est radial.
champ électrique :(point
extérieur)
flux envoyé
à travers la sphère
S
de rayon r : définition du flux
: F=
4pr2E
th. de gauss :
charge
intérieure à S=
charge de S =4/3
pR3r.
F=
4/(3e0)
pR3r
E
=
R3r/(3e0r2). (
proposition n°1 ).
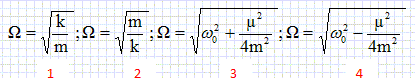
 (
proposition n°2 )
(
proposition n°2 )

 Par raison de symétrie, le champ est radial.
Par raison de symétrie, le champ est radial.