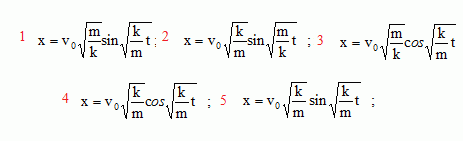Oscillateur
horizontal.
Les frottements sont négligés ; on note k la raideur du ressort ; on
appelle x l'abscisse du centre d'inertie du solide S de massse m.
La position d'équilibre O est choisie comme origine.
A la date t=0, x=0, la vitesse est v0 orientée dans le
sens de l'axe.
Quelle est
l'équation horaire du mouvement de S ?
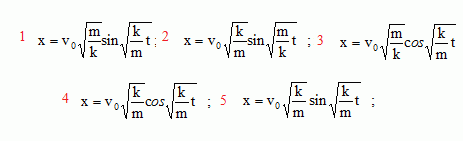
On pose w2 = k/m
; w = (k/m)½.
L'équation horaire est de la forme x= A sin(wt + f ).
A t = 0, x=0 d'où A sin f =0 ; A est l'amplitude non
nulle, donc f = 0 ou f = pi radians.
Vitesse v = dx/dt = A w cos (wt + f ).
v(t=0) = v0 = A w cos f ; v0 étant
positive f = 0 et A = v0
/ w = v0(m/k)½.
x = v0(m/k)½ sin((k/m)½t) ; expression 1.
|
Pendule simple.
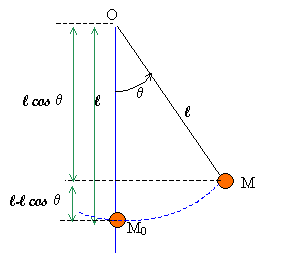
On le lâche sans vitesse initiale de telle manière que q0 =30°.=
m = 250 g ; l=30 cm ; g= 9,8 N /kg.
Que vaut la tension ( en N ) du fil au passage à la position d'équilibre ?
( 2,50 ; 3,11 ; 4,60 ; 7,20 ; 11,0 )
Ecrire le théorème de l'énergie cinétique entre la position initiale et la position q=0 :
Travail moteur du poids en descente ; la tension du fil, perpendiculaire à la vitesse, ne travaille pas.
Puis écrire la seconde loi de Newton suivant l'ase n .
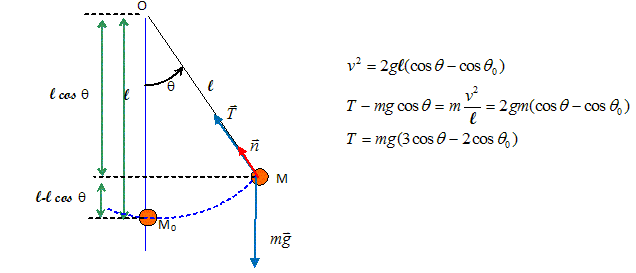
Au passage à la position d'équilibre q = 0 : T = mg(3-2cosq0)
T = 0,25*9,8(3-2*cos30) = 3,11 N.
|
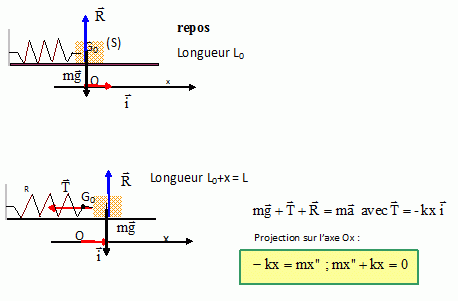
Oscillateur élastique horizontal.
Caractéristiques : k = 10 N/m ; masse m = 400 g ; vitesse maximale vmax = 0,5 m/s. Frottements négligés.
Quelle est son amplitude en cm ?
(10 ; 20 ; 5 ; 7,5 ; 12,5)
Lorsque la vitesse est maximale, l'oscillateur passe par la position
d'équilibre( choisie comme origine de l'énergie potentielle élastique) ;
l'énergie mécanique est sous forme cinétique : EM = ½mv2max.
Lorsque la vitesse est nulle, l'abscisse du centre d'inertie de la masse m est égale à l'amplitude A ;
l'énergie mécanique est sous forme potentielle élastique : EM = ½kA2.
La conservation de l'énergie mécanique conduit à : ½mv2max=½kA2.
mv2max=kA2 ; A = (m/k)½vmax = (0,4 / 10)½ *0,5 =0,1 m = 10 cm.
Pendule simple lâché avec une vitesse initiale.
Caractéristiques : longueur L =0,62 m ; masse m =100 g ; vitesse initiale : v0 =0,75 m/s ; inclinaison initiale q0 = 12 °. Frottements négligés.
Quelle est l'énergie potentielle maximale ( en mJ) du système ?
(54 ; 41,4 ; 90,4 ; 77,2 ; 18,3)
Lorsque la vitesse est nulle, l'énergie mécanique se trouve sous forme potentielle : EM = mghmax.
Initialement l'énergie mécanique se trouve sous forme cinétique et potentielle : EM =mgL(1-cosq0) +½mv20.
La conservation de l'énergie mécanique conduit à : mgL(1-cosq0) +½mv20 =mghmax.
mghmax.=0,1*9,8*0,62(1-cos12) + 0,5*0,1*0,752=0,01328 +0,02813= 0,0414 J = 41,4 mJ.
Pendule.
La bobine parcourue par un courant se comporte comme un aimant.
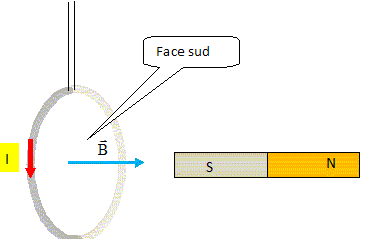
La bobine est déviée vers la gauche. Vrai.
Deux poles de même nom se repoussent.
Le pendule n'est pas dévié. Faux.
Le pendule à tendance à tourner sur lui même. Faux.
La
bobine s'éloigne vers la gauche, puis se retourne afin de présenter sa
face nord au pôle sud de l'aimant ; puis elle est attirée vers l'aimant
et s'immobilise.
La bobine est déviée vers la droite. Faux.
La bobine est déviée hors du plan de la figure. Faux.
Oscillateur élastique horizontal.
Caractéristiques : m = 256 g ; raideur k = 78 N/m ; abscisse initiale x0 = +2 cm ( ressort étiré) ; vitesse initiale nulle.
Quelle est l'équation horaire( en S.I ) du mouvement du solide ?
x(t) = 0,02 sin(0,36t) ; x(t) = -0,02 cos(0,36t) ; x(t) = 0,04 cos(17,5t) ; x(t) = 0,04 sin(17,5t) ; x(t) = 0,02 cos(17,5t).
Pulsation w = (k/m)½ =(78 /0,256)½ =17,455 ~17,5 rad/s.
L'équation horaire est de la forme x(t) = A cos (wt + f )
x(t=0=) = 0,02 = A cos f ; A étant l'amplitude positive, f = 0.
x(t) = 0,02 cos (17,5 t).
Quelle est la vitesse ( m/s) si x=0,5 cm ?
(220 ; 0,34 ; 0,26 ; 870 ; 0,17 ).
x(t) = 0,005=0,02 cos (17,5 t) ; cos (17,5 t) = 0,005/0,02 =0,25 ; 17,5 t = 1,318 rad.
v(t) = dx(t) / dt = 0,02*17,5 (-1) sin(17,5 t)
v(t) = 0,02*17,5 sin 1,318 = 0,339 ~0,34 m/s.