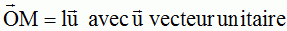Energie mécanique : glissade sur un plan incliné.

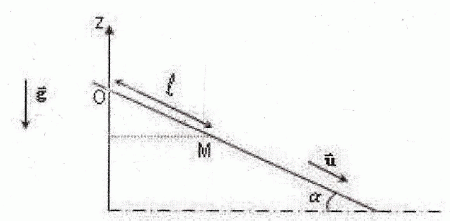
Mouvement sans frottement. Une coordée de deux alpinistes, attachés l'un à l'autre par une corde de nylon extensible de longueur au repos l0, grimpe une pente de glace. Les deux alpinistes se trouvent au point O ; l'un d'eux perd l'équilibre et part en glissade à partir de O avec une vitesse initiale nulle. l'autre alpiniste reste attaché au point O. La corde se tend, sans que soit dépassée sa limite d'élasticité. La corde est dite au repos lorsqu'elle ne subit pas de traction. Lorsque sa longueur l est supérieure à l0, on assimile l'action exercée par la corde à celle d'un ressort de masse négligeable, de longueur au repos l0, de raideur k, dont chacune des extrémités est reliée à un des alpinistes. L'alpiniste qui chute est assimilé à un point matériel ponctuel de masse m, dont la position à l'instant t est représentée par 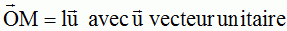Exprimer l'énergie potentielle de pesanteur Epl du glisseur en fonction de m, g, l et a. On prend Epl(l=l0) = 0. Altitude de O : zO= l0 sin a ; altitude de M : zM = (l0 -l)sin a. 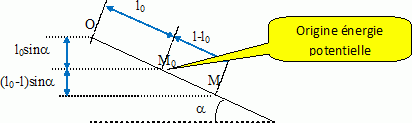Epl (M)= mg zM = mg (l0 -l)sin a. Dans le cas où l > l0, exprimer l'énergie potentielle élastique Epé de l'ensemble glisseur + corde en fonction de k, l et l0. Epé = ½k(l-l0)2. Ecrire l'énergie potentielle totale Ep de l'ensemble glisseur + corde. Corde non tendue : Ep = Epl (M)= mg (l0 -l)sin a. Corde tendue : Ep = Epl (M) + Epé =mg (l0 -l)sin a + ½k(l-l0)2. Existe t-il une position d'équilibre possible pour le glisseur ?  Si oui, préciser la valeur le de l correspondante ainsi que la nature de cet équilibre. A l'équilibre, la valeur de l'énergie potentielle est minimale. Dériver Ep par rapport à l et rechercher la valeur de l qui annule Ep. Corde non tendue : dEp/dl = -mgsin a. La dérivée ne s'annulle pas : pas de position d'équilibre. Corde tendue : dEp/dl = -mgsin a + k(l-l0) dEp/dl =0 si mgsin a = k(lé-l0) lé-l0= mgsin a / k ; lé= l0 + mgsin a / k. Il existe donc une position d'équilibre. Recherche de la dérivée seconde : d2Ep/dl2= k La dérivée seconde est positive : l'équilibre est stable.   Donner l'allure du graphe Ep en fonction de l. 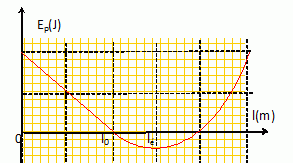Décrire qualitativement le mouvement du glisseur. Corde non tendue : mouvement rectiligne uniformément accéléré. Corde tendue : mouvement oscillatoire périodique autour de la position d'équilibre stable. Quelle sera l'énergie cinétique Ecé du glisseur à la position repérée par lé ?  Energie mécanique initiale E(O) = Epl (O)= mg zO = mg l0 sin a. Energie mécanique à la position d'équilibre : Eéqui =Ecé +Ep équi = Ecé + mg (l0 -lé)sin a + ½k(lé-l0)2. or mgsin a = k(lé-l0) d'où : Eéqui = Ecé -k(lé-l0)2+ ½k(lé-l0)2 = Ecé -½k(lé-l0)2. En absence de frottement l'énergie mécanique se conserve : mg l0 sin a = Ecé -½k(lé-l0)2. Ecé = mg l0 sin a +½k(lé-l0)2. Quelle sera la distance maximale lm atteinte par le skieur au bout de sa corde ? Ep = mg (l0 -lm)sin a + ½k(lm-l0)2. L'énergie cinétique est nulle pour l = lm. Energie mécanique  :  E= Ep = mg (l0 -lm)sin a + ½k(lm-l0)2. Conservation de l'énergie mécanique : mg l0 sin a = mg (l0 -lm)sin a + ½k(lm-l0)2. -mg lmsin a + ½k(lm-l0)2= 0. ½klm2 -kl0lm-mg lmsin a +½kl02=0. lm2 -2l0lm-mg / k lmsin a +l02=0. Or mgsin a = k(lé-l0) d'où : lm2 -(l0+le)lm +l02=0. Discriminant : D =(l0+le)2 -4l02 ; on retient la racine positive : lm =½[(l0+le) +( (l0+le)2 -4l02)½]. Quelle sera la vitesse maximale vm atteinte par le glisseur ? Lorsque l'énergie potentielle est minimale, l'énergie cinétique est maximale ½mvm2. ½mvm2 = mg l0 sin a +½k(lé-l0)2. vm= [2g l0 sin a +k/m(lé-l0)2]½. A.N : a = 30° ; m = 60 kg ; g = 10 m s-2 ; k = 300 N/m ; l0 = 24 m. lé= l0 + mgsin a / k= 24 +60*10 sin 30 / 300 =  25 m. lm =½[(l0+le) +( (l0+le)2 -4l02)½] = lm =½[49 +( 492 -4*242)½]=29,4 m. vm= [2g l0 sin a +k/m(lé-l0)2]½ =[20*24 sin 30 +300/60(25-24)2]½ =15,6 m s-1. Ecé = mg l0 sin a +½k(lé-l0)2= 600*24*sin 30 +150=7,35 103 J. Frottements non négligés : Les frottements sont supposés proportionnels à la vitesse. Décrire qualitativement le mouvement du glisseur. Quelle sera la position finale du skieur ? Corde non tendue : mouvement rectiligne  accéléré. Corde tendue : mouvement oscillatoire pseudo-périodique ( l'amortissement est supposé faible ) autour de la position d'équilibre stable. Le skieur finira par s'immobiliser à la position d'équilibre. Exprimer le travail W des forces de frottements. Calculer W. Le travail des frottement est égal à la diminution de l'énergie mécanique. Energie mécanique initiale E(O) = Epl (O)= mg zO = mg l0 sin a. Energie mécanique à la position d'équilibre : Eéqui =Ecé -½k(lé-l0)2 avec  Ecé = 0 ( arrêt ). W = -½k(lé-l0)2 -mg l0 sin a. W = -0,5*300*(25-24)2 -60*10*0,24 sin 30 = -222 J. .

retour -menu