Circuit électrique antirésonant : concours Mines  2010

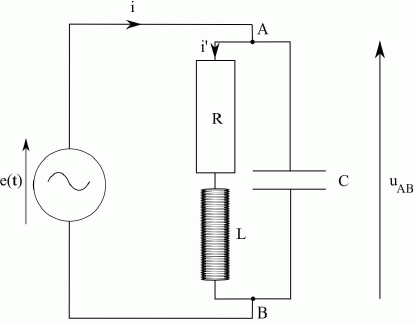
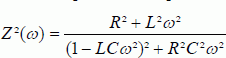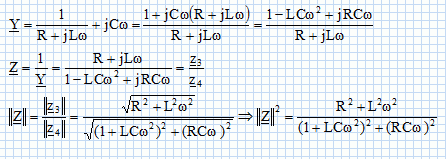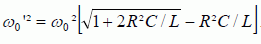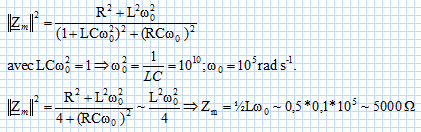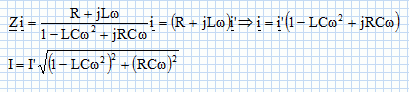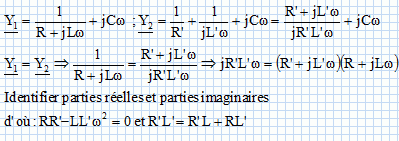On s’intéresse dans cette partie au circuit (C1) suivant, alimenté par une source de tension alternative de f.e.m. e(t) =E0 cos(wt). La bobine idéale a une inductance L (L = 0,10 H) , le conducteur ohmique une ré-sistance R (R = 10 Ω) et le condensateur une capacité C (C = 1,0 nF). On notera j le nombre complexe tel que j² = -1. Questions préliminaires. Qu’appelle-t-on résonance en intensité dans un circuit ? Lorsque la fréquence w de l'excitateur ( la tension alternative de fem e(t) ) est égale à la fréquence propre w0 du résonateur ( le circuit RLC), la valeur efficace de l'intensité passe par une valeur d'autant plus importante que la résistance R est plus faible. Par analogie que peut-on appeler antirésonance en intensité ? L'impédance du dipôle est maximale et la valeur efficace de l'intensité est nulle.   Dans le cas du circuit R,L,C série quelle est l’expression de l’impédance complexe Z du dipôle constitué par l’association de ces trois éléments ? Quelle est l’expression du module Z(w) de cette impédance complexe ? Impédance complexe Z = R + jLw +1/ (jCw)  = R + j( Lw -1/ (Cw)) Module de Z  : Z(w) = [R2 +(Lw -1/ (Cw))2]½. À quelle condition sur Z(w) a-t-on résonance en intensité dans le circuit série ? Pour quelle valeur ω0 de la pulsation ce phénomène se produit-il ? Que peut-on dire du déphasage de l’intensité dans le circuit par rapport à la tension aux bornes du conducteur ohmique à la résonance ? A la résonance d'intensité, l'impédance Z(w) du dipôle est minimale égale à R, ce qui se traduit par :  Lω0 =1/ (Cω0)  ou encore ω0 = [1/(LC)]½. L'intensité et la tension aux bornes du conducteur ohmique sont en phase. Étude du circuit anti-résonant.  Calculer l’impédance complexe du dipôle AB.  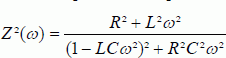En déduire que le module au carré de l’impédance du dipôle AB s’écrit : Impédance complexe de la branche RL : Z1 = R + jLw ; impédance complexe de la branche contenant le condensateur : Z2 = 1/(jCw). En dérivation les admittances complexes s'ajoutent : ( admittance : inverse de l'impédance). 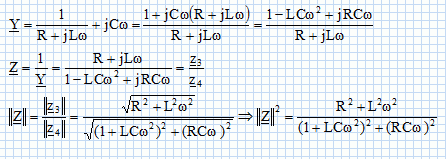Une dérivation non demandée montre que Z(w) passe par un extremum pour une pulsation ω'0 qui vérifie : 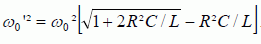Vérifier que R2C / L << 1. R2C / L  =102*1,0 10-9 / 0,1 = 10-6, valeur très inférieure à 1. Montrer que w'0 ~w0(1-f(R, L, C)) où w0  est  la pulsation de résonance du circuit RLC série et f(R, L, C) une fonction de R, L et C que l'on précisera. (1 + e) a ~ 1 +ae si e est petit devant 1 ; (1+2R2C / L)½ ~ 1+R2C / L~ 1. Par suite w'02 ~w02(1-R2C / L ) ; w'0 ~w0(1-R2C / L )½ ~ w0(1-½R2C / L ). Calculer numériquement f(R, L, C). Que peut-on dire de w'0 et w0 ? f(R, L, C) = ½R2C / L =5 10-7 ; w'0 ~w0. Dans toute la suite on pourra utiliser l’approximation w'0 ~w0. Donner les limites de Z(ω) en 0 et en l’infini. Donner l’allure des variations de cette fonction en précisant la valeur de Z(ω'0) = Zm. Justifier qu’on parle d’ « antirésonance » dans ce cas. R2 + L2w2 tend vers R2 si w tend vers zéro. (1-LCw2 ) + (RCw)2 tend vers 1 si w tend vers zéro. par suite Z(w) tend vers R= 10 W si w tend vers zéro. R2 + L2w2 équivalent à   L2w2 si w tend vers l'infini. (1-LCw2 )2 + (RCw)2 équivalent à   (LCw2 )2 si w tend vers l'infini. par suite Z(w) équivalent à  L/  (LCw2 ) tend vers zéro si  w tend vers l'infini. 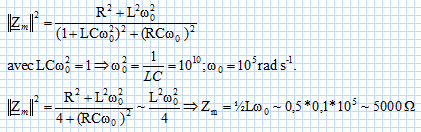La valeur de l'impédance Zm étant très grande, l'intensité efficace du courant sera très faible, d'où le terme d'antirésonance. Établir une relation entre i, i', R, L ,C et ω. 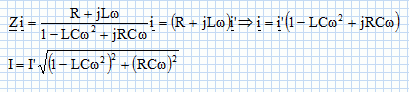(R+jLw) i' = Z i ; Notons respectivement I et I’ les amplitudes de i et i’. Montrer qu’à l’antirésonance le courant I’ dans la branche constituée par la bobine et le conducteur ohmique est beaucoup plus grand que celui I dans le circuit général. I(w0) =I'(w0) RC w0= 10*10-9*105 I'(w0) ; I(w0) =10-3I'(w0) ou I'(w0) = 1000 I(w0). Soit (C2) le circuit suivant, constitué de l’association parallèle d’une bobine idéale d’inductance L’, d’un conducteur ohmique de résistance R’ et d’un condensateur de capacité C, identique à celui intervenant dans le circuit (C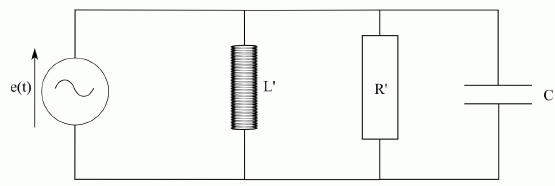 Montrer qu’au voisinage de l’antirésonance les circuits (C1) et (C2) peuvent être considérés comme équivalents et calculer alors L’ et R’ pour que cette équivalence soit réalisée. On utilisera avantageusement les admittances pour traiter cette question. 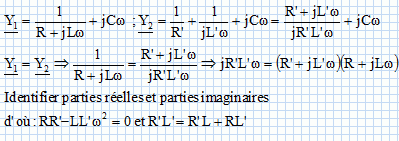10 R' = 109L' ; R' = 108L' et R'L' = 0,1 R' +10 L'. 108L'2 - 10L'-107L'=0  ; L' = 0,1 H et R' = 107 W.

menu