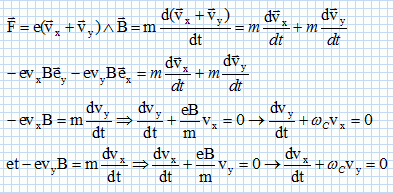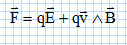Un
cyclotron est un accélérateur de particules qui utilise l’action
combinée d’un champ électrique E et d’un champ magnétique B afin
d’accélérer des particules chargées.
Dans le cadre du traitement de certains cancers crâniens et oculaires,
notamment chez les enfants, la radio-thérapie classique est
avantageusement remplacée par la protonthérapie (envoi de protons
rapides sur les cellules cancéreuses en vue de les détruire) qui
minimise les dégâts occasionnés aux tissus biologiques entourant la
tumeur. Les protons à envoyer dans la tumeur sont accélérés à l’aide
d’un cyclotron. En France, il existe deux principaux centres utilisant
cette technique : Nice (protons de 65 MeV) et Orsay (protons de 200
MeV). On va ici s’intéresser au principe d’un cyclotron qui pourrait
être utilisé dans ce cadre.
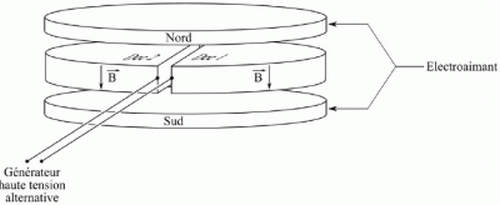
Le cyclotron est constitué de deux demi-cylindres horizontaux de rayon
R très légèrement écartés et creux, les « Dees », au sein desquels
règne un champ magnétique B uniforme et constant d’intensité B = 1,67
T. À l’intérieur des Dees, il règne un vide poussé. Entre ces deux Dees
une tension haute fréquence de valeur maximale U = 100 kV crée un champ
E perpendiculaire aux faces en regard des Dees.
|
Des protons de masse mP = 1,67.10–27 kg et de charge e = 1,60.10–19 C, animés d’une vitesse horizontale négligeable, sont injectés au point A0 de l’espace séparant les deux Dees.
On rappelle l’expression de la force de Lorentz F que subit une
particule de charge q, animée d’une vitesse v lorsqu’elle est placée
dans une zone où règne un champ électromagnétique :
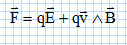
Dans tout le problème, la force de Lorentz sera la seule force prise en compte.
|
Étude du mouvement dans les Dees.
On étudie le mouvement d’un proton qui pénètre pour la première fois dans le Dee 1 en A avec la vitesse v1, de valeur V1.
Montrer que le mouvement du proton dans un Dee est uniforme.
Le poids du proton est négligeable devant la force de Lorentz. La force
de Lorentz, perpendiculaire à la vitesse, ne travaille pas. L'énergie
cinétique du proton, et en conséquence la valeur de la vitesse, restent
constantes. Le mouvement est donc uniforme.
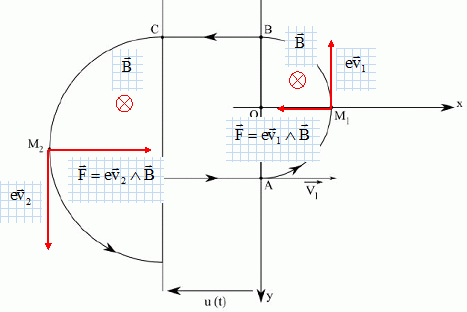
Représenter sur le schéma 1 de la feuille annexe les vecteurs champ
magnétique dans chacun des Dees, les vecteurs vitesse et force de
Lorentz aux points M1 et M2.
Par
application de la relation fondamentale de la dynamique, établir le
système d’équations différentielles couplées auxquelles satisfont les
composantes Vx et Vy de son vecteur vitesse v. On introduira la pulsation cyclotron ωC = eB/m.
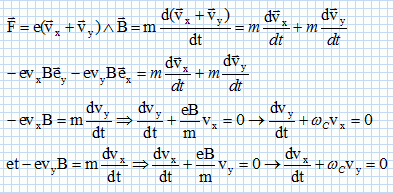
Montrer que la trajectoire du proton dans le Dee 1 est un cercle de rayon R1=v1/wC.
d2y/dt2+wCdx/dt = 0 et d2x/dt2+wCdy/dt = 0.
Soit p(t) = x(t) + jy(t) avec j2=-1 ; dp(t)/dt = dx(t)/dt + jdy(t) /dt ; d2p(t)/dt2 =
d2x(t)/dt2 +
jd2y(t) /dt2
dp(t)/dt = 1/ wC
(-d2y/dt2
+jd2x/dt2)=
1/ wC
(j2d2y/dt2
+jd2x/dt2)
dp(t)/dt = j/ wC
(jd2y/dt2
+d2x/dt2) ;
dp(t)/dt
=j/ wCd2p(t)/dt2.
Quelles sont les deux conditions
initiales sur p(t) ?
A t=0, le proton est en O avec une vitesse initiale v1 dirigée suivant Ox.
p(0) = 0 ; dp(0)/dt = dx(0)/dt + jdy(0) /dt=
v1 ; dp(0)/dt =v1 .
Résoudre
l'équation différentielle et déterminer
p(t).
dp(t)/dt
=j/ wCd2p(t)/dt2
s'écrit :
d2p(t)/dt2
+jwCdp(t)/dt
=0
équation
caractéristique : r2 +
jwC r=0
; solutions r1=0 et r2= -
jwC.
p(t) = A + B exp(-
jwCt)
à t = 0 : 0 = A+B soit B =
-A
dp(t)/dt = - jwCB
exp(- jwCt)
; dp(0)/dt = v0=- jwCB
; B = jv0/wC
p(t) =
jv0/wC
( exp(- jwCt)-1).
En déduire x(t) et
y(t).
exp(- jwCt)
= cos(wCt)
-j sin(wCt)
; p(t) =
jv0/wC[cos(wCt)-1
-j sin(wCt)]
p(t)
=v0/wCsin(wCt)
+ jv0/wC[cos(wCt)-1]
= x(t) + jy(t)
x(t) =
v0/wesin(wet)
;
y(t) =
v0/we[cos(wet)-1].
La trajectoire est un cercle.
Démontrons que le rayon
est R1 =mv1/(eB).
y+v1/wC
=v0/wCcos(wCt)
x2+(y+v0/wC)2
= [v0/wC]2
[sin2(wCt)
+cos(wCt)2
] = [v0/wC]2
centre du cercle A (0 ;
-v0/wC)
; rayon R1 = v1/wC
= mv1/(eB).
On
admet que ce résultat se généralise et que la trajectoire lors de la
nième traversée d’un Dee sera circulaire uniforme de rayon Rn=vn/wC.
Exprimer, en fonction de Rn la distance d parcourue dans un Dee lors du nième demi-tour.
d = p Rn ( demi circonférence de rayon Rn)
Montrer
que la durée Δt de parcours de la trajectoire dans un Dee est
indépendante de la vitesse du proton et donner son expression en
fonction de m, e et B.
Dt =d /vn = d / (Rn wC ) = p Rn / (Rn wC )= p / wC = m p / (eB).
|
Étude du mouvement entre les Dees.
Entre les Dees, qui sont très faiblement écartés, le proton décrit une trajectoire rectiligne et est accéléré.
Préciser la direction et le sens que doit avoir le champ électrique E entre les Dees quand le proton décrit A0A,
puis BC. Dans chaque cas, quel doit être le signe de la tension u
pour que les protons soient toujours accélérés quand ils passent entre
les Dees ?
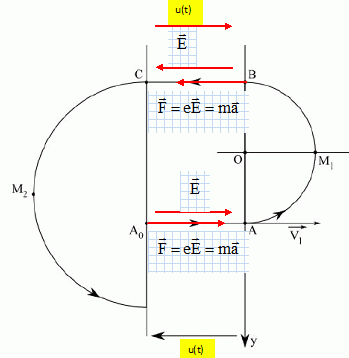
Le champ électrique pointe vers le plus petit potentiel : entre A0 et A u(t) a le sens de la flèche indiquant u(t).
Entre B et C, u(t) doit avoir le sens contraire.
Le schéma 2 de l’annexe fournit le graphe de la tension u(t). Noter sur ce graphe :
- le moment où le proton passe de A0 à A, puis lorsqu’il passe de B à C ;
- la durée Δt de parcours de la trajectoire dans chacun des Dees.
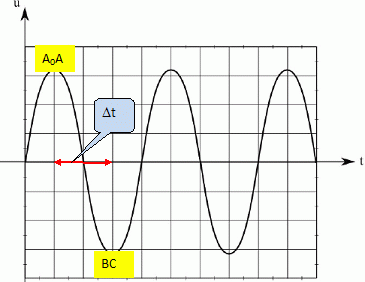
Pour une accélération maximale,
à chaque demi tour, la tension alternative doit
changer de signe et prendre sa valeur maximale.
Donner la relation entre la période T de la tension u(t) et la durée Δt ; en déduire l’expression de la fréquence f de u(t) en fonction de m, e et B.
T = 2 Dt si on néglige la durée du passage entre les Dees.
f = 1/ T = 1 / (2 Dt) = eB / (2mp)
|
|