|
|
Varistance.
On considère un dipôle nommé varistance, de caractéristique U = C Iß
avec U tension aux bornes du dipôle, I intensité du courant qui la
traverse, C et ß des constantes positives.
Exprimer
C en fonction de I, ß et RS. La
résistance statique est définie par RS = U / I.
C = U / Iß ; U = RS I ; C
= RS I / Iß ; C = RS I1-ß.
A.N : I = 0,1 A ; ß
=0,2 ; RS=100 ohms.
Calculer C et U.
C = 100 *0,10,8
=15,85 ~16 V A-0,2.
U = RS I
=100*0,1 = 10 V.
Déterminer
la relation entre résistance statique et résistance dynamique.
La résistance dynamique est définie par Rd
= dU/dI = C ß Iß-1.
Or C = RS I1-ß
; Rd = ß RS I1-ß Iß-1= ß RS ;
Rd = ß RS .
|
|
Un
générateur de fem E et de résistance interne négligeable débite dans un
circuit constitué par une résistance R = 100 ohms et la
varistance précédente placées en série.
Exprimer E en
fonction de U, C et des résistances.
Additivité des tensions : E = RI + U
Or Iß
= U/C ; I = (U/C)1/ß ; par suite : E = R(U/C)1/ß + U.
|
Exprimer la variation dE en
fonction de dI puis de dU en introduisant Rd.
E = RI + U = RI +C Iß
dE
= RdI + C ß Iß-1 dI = (R + C ß Iß-1
) dI.
avec dU = Rd dI : dE = (R
+ C ß Iß-1
) / Rd dU.
Exprimer le
coefficient de stabilisation S défini par S = d (lnE) / d(lnU) en
fonction de R, RS et Rd puis en fonction de ß et
de x = U/E.
d(lnE)
= dE / E ; d(lnU) = dU / U ; S = U / E dE/dU.
dE/dU
= (R +
C ß Iß-1
) / Rd
S = U (R +
C ß Iß-1
) / (ERd) avec CIß-1
= U/I = RS.
S = U( R +RSß) /
(ERd) avec Rd = ß RS.
S = U( R
+Rd) /
(ERd) = U/E ( R /Rd+1).
S = x ( R /Rd+1).
R= (E-U) / I ; Rd
=ß RS=ßU / I ; R /Rd =(E-U) / (ßU) = (E/U-1) / ß = (x-1) / ß.
par suite : R /Rd+1= (x-1) / ß +1et S = x [(x-1) / ß +1 ].
Calculer S en
fonction de x si ß = 0,2.
S = x[(x-1) / 0,2 +1]= x [5(x-1)+1] = x (5x-4).
Si on remplace la varistance par un résistor de résistance R',
montrer
que le montage avec varistance est supérieur au montage avec le
résistor en ce qui concerne la stabilisation en tension lorsque E
varie légèrement autour de sa valeur nominale.
U
= R'I ; E = RI+U = RU / R' + U ; E = U( R / R' +1)
dE = dU( R / R' +1)
S = U/E (R / R' +1) ; S = x(R / R' +1)
R = (E-U)/I ; R' = U/I ; R/R' =(E-U) / U = E/U-1 = x-1
R / R' +1 = x ; S = x2.
Le coefficient de stabilisation S est bien supérieur dans le cas de la
varistance.
Un
générateur de résistance interne R0 délivre une fem
sinusoïdale e(t) de pulsation w
et d'expression e(t) = 2½E sin(wt). Il est relié aux bornes d''un
résistor de résistance R.
Donner
l'expression de la puissance moyenne P(R), dissipée dans le résistor.
Tension aux bornes du résistor : u(t) = R i(t) = e(t) -R0i(t)
; i(t) = e(t) / (R+R0).
u(t) = R/
(R+R0) e(t)
Puissance dissipée dans le résistor : P = u(t) i(t) = R/
(R+R0)2 e2(t)
Puissance moyenne :
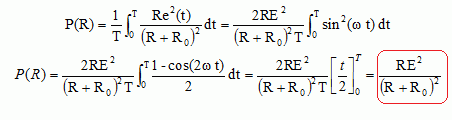
Montrer
qu'elle passe par un maximum.
Calculer
la valeur Rm correspondante
ainsi que la puissance Pm correspondante.
Dériver P(R) par rapport à
R en posant u = R , v =(R+R0)2 ; u' = 1 , v' =
2(R+R0).
dP/dR =(u'v -v'u)/v2 ; elle s'annule si u'v
= v'u ; (R+R0)2 =2R(R+R0) soit Rm = R0.
Si R tend vers zéro, P(R) tend vers zéro ; si R tend vers l'infini,
P(R) tend vers zéro : il s'agit donc d'un maximum.
Pm
=R0E2 / (4R02)= E2 / (4R0).
A.N
: E = 220 V ; R0 = 10 ohms ; w = 314 rad/s.
Pm =2202 / 40 =1210 W = 1,21 kW.
|
|
On insère en série avec le résistor une bobine pure d'inductance L=0,1
H.
Calculer en fonction
de R la puissance P' dissipée dans le résistor.
Impédance du dipole R+R0 L : Z = [(R+R0)2
+(Lw)2]½.
intensité efficace I =E / Z = E [(R+R0)2 +(Lw)2]-½.
P' = RI2 = RE2 / [(R+R0)2
+(Lw)2].
Calculer la valeur R'm pour laquelle elle
est maximale.
Dériver P' par rapport à R
en posant u = R , v =(R+R0)2
+(Lw)2 ; u' = 1 , v' = 2(R+R0).
dP/dR =(u'v -v'u)/v2 ; elle s'annule si u'v
= v'u ; (R+R0)2 +(Lw)2 =2R(R+R0)
(R +10)2+(0,1*314)2 =2R(R+10)
R2+20 R+100+986=2R2 +20R
1086 = R2 ; R = R'm =1086½
=32,95 ~ 33
ohms.
Montrer que quel que
soit R, le rapport P'/P est inférieur à 1.
P' = RE2
/ [(R+R0)2 +(Lw)2]
; P =RE2 / (R+R0)2 ;
P'/P =(R+R0)2 / [(R+R0)2 +(Lw)2]
Le dénominateur étant toujours supérieur au numérateur, le rapport P'/P
est inférieur à 1.
On branche le générateur précédent aux bornes AB d'un transformateur
parfait.

Rapport des valeurs efficaces UCD / UAB = U2/U1
= n.
La puissance moyenne au primaire est égale à celle du secondaire.
Le facteur de puissance est égal à l'unité aussi bien au primaire
qu'au secondaire.
Déterminer le
rapport des valeurs efficaces ICD / IAB = I2/I1.
Puissance apparente au primaire : U1 I1
Puissance apparente au secondaire : U2 I2.
U1 I1= U2 I2 d'où : I2
/ I1 = U1 / U2
= 1/n.
Exprimer la
puissance absorbée par le résistor en fonction de n, E, R
et R0.
Le résistor apsorbe la puissance P = R I22 ;
U1 = E-R0I1 = U2 /n =RI2/n
avec I1 = n I2.
E-R0 n I2 =RI2/n ; I2
= E / [R0 n +R/n]=nE / [R0 n2 +R]
P =RE2n2 / [R0 n2 +R]2.
Pour quelle valeur
de n cette puissance est-elle maximale ?
Dériver P par rapport à n et annuler cette dérivée.
On pose u = n2 , v = [R0 n2 +R]2
; u' = 2n , v' = 2[R0 n2 +R]2R0n
DP/dn = (u'v -v'u) / v2 = 0 ; u'v =v'u
2n[R0 n2 +R]2 =4R0n3[R0
n2 +R]
R0 n2 +R =2R0n2 ; n = (R / R0)½.
|
.
|
|