Remontée d'une bulle, force centrale : concours itpe

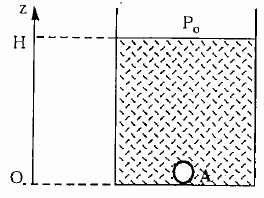
Remontée d'une bulle. Au fond d'un puits rempli d'eau, de profondeur H, ouvert  à la pression atmosphérique P0,  se forme au point A une bulle de gaz de masse volumique µa non soluble dans l'eau. On désigne par g l'accélération de la pesanteur et par µ la masse volumique de l'eau. La norme de la force de frottement que subit la bulle lors de sa montée est donnée par : f = 6 p nR v où R désigne le rayon de la bulle, n le coefficient de viscosité de l'eau et v la vitesse de la bulle.   Ecrire l'équation dynamique de la bulle en projection sur l'axe Oz. La bulle est soumise  à son poids P = m g avec m = 4/3 pR3µa, verticale vers le bas ; à la poussée d'Archimède F = 4/3 pR3µ g, verticale, vers le haut ; à la force de frottement f, verticale vers le bas. 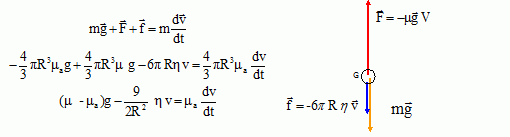La simplifier si µ >> µa. µg - 4,5hv /R2 = µa dv/dt. La bulle atteind rapidement une vitesse limite notée vlim.  Donner son expression en fonction des données. dvlim/dt = 0, le mouvement est rectiligne uniforme. µg - 4,5h vlim /R2 =0 ;  4,5h vlim =µgR2 ;              vlim =µgR2 / (4,5 h). A.N : µ =1000 kg m-3 ; g = 10 m s-2 ; h = 10-3 SI ; R = 1 mm. vlim =1000*10*(10-3)2 / (4,5 * 10-3) =10/4,5 = 2,22 m s-1~ 2 m s-1. En supposant que le volume de  la bulle est constant, donner l'expression de la durée T  nécessaire  à sa montée jusqu'à la surface. La dure de la phase " mouvement transitoire " est négligeable devant la durée de la montée  à vitesse constante. T = H / vlim = 4,5 h H / (µgR2). A.N : H = 10 m.T = 10 / 2,22 = 4,5 s. Dans cette partie on tient compte du changement de taille de la bulle au cours de la montée. Donner l'expression  de la pression PA du gaz dans la bulle quand elle se forme  au point A.   PA = P0 + µgH. Donner l'expression  de la pression P(z) du gaz dans la bulle quand elle atteint la cote z.      P(z) = P0 + µg(H-z) ; or  P0 = PA - µgH. P(z) =PA - µgH+ µg(H-z) ; P(z) =PA -µgz. En supposant que la température reste constante au cours de la montée et que le gaz se comporte comme un gaz parfait, donner l'expression du volume V de la bulle à la cote z en fonction de PA, du volume initial VA et de P(z). A température et à masse de gaz constantes, la loi de Mariotte s'écrit : PA VA =P(z) V ; V = PA VA / P(z). En déduire l'expression du rayon r(z) de la bulle en fonction de R, PA, g et z. V = 4 /3 p r3(z) ; VA = 4 /3 p R3 ; P(z) =PA -µgz. 4 /3 p r3(z) =PA 4 /3 p R3 / (PA -µgz) r3(z) =PAR3 / (PA -µgz) ; r(z) = R [ PA/ (PA -µgz) ]1/3.     Calculer numériquement le rapport VH / VA si P0 = 1 bar. VH = PA VA / P(H) ; VH / VA= PA  / P(H) ; PA = P0 + µgH = 1 + 1 = 2 bar ; P(H) =PA -µgH = P0 = 1 bar. VH / VA=2. Puisque le rayon de la bulle  dépend de z, la vitesse limite dépend également de z. On admettra qu'à chaque instant la bulle se déplace  à la vitesse limite Vlim(z) correspondant  à sa taille. Donner l'expression de Vlim(z) en fonction de Vlim, PA, µ, g et z.  Vlim(z) = µg r2(z) / (4,5 h)   vlim =µgR2 / (4,5 h) ; r(z) = R [ PA/ (PA -µgz) ]1/3 ; Vlim(z) = µg R2[ PA/ (PA -µgz) ]2/3  / (4,5 n) ; Vlim(z) = vlim [ PA/ (PA -µgz) ]2/3. Mouvement elliptique. Les vecteurs sont écrits en gras et en bleu. Un point matériel de masse m se déplace dans le plan xOy. Son vecteur position est donné par : r = a cos ( wt) i + b sin (wt) j où a, b et w sont des constantes positives telles que a > b. 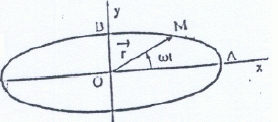Trouver la trajectoire de ce point.  Dans le repère xOy : abscisse de de ce point x = a cos ( wt) ; ordonnée de ce point y = b sin (wt) (x/ a)2 + (y/b)2 = cos2( wt) + sin2 (wt) =1. Le point M décrit une éllipse. Montrer que la force agissant sur celui-ci  est en tout point dirigée vers l'origine. Dériver deux fois x et y par rapport au temps : x' = -a w sin (wt) ; y' = b w cos ( wt) x" = -aw2cos ( wt) ; y" = -bw2sin ( wt) ; x" = -w2x ; y" = -w2y ; Expression de l'accélération : a = -w2 x i  -w2 y j. Expression de la force agissant sur le point : F= ma = -mw2 (x i  +y j) F= -mw2 r. Le point M est soumis  à une force centrale. Calculer l'énergie cinétique en un point quelconque de la trajectoire. Ec = ½ mv2 avec v2 =x'2 +y'2. Ec = ½ mw2 [ a2 sin2(wt) + b2 cos2(wt) ]   Calculer le travail fourni par la force pour déplacer le point matériel  de A à B. Travail élémentaire de la force : dW = F. dr = -mw2 r . dr =-½mw2 dr2.  dW =-d[½mw2 r2] ; W = ½mw2  (rA2- rB2) Or rA = a  ; rB = b  ; W = ½mw2  (a2- b2). Vérifier le théorème de l'énergie cinétique. Ec = ½ mw2 [ a2 sin2(wt) + b2 cos2(wt) ] Au point B:  Ec(B) = ½ mw2a2 ; au point A :  Ec(A) = ½ mw2b2 Variation de l'énergie cinétique : Ec(B)-Ec(A) =½mw2  (a2- b2). Cette variation de l'énergie cinétique est bien égal au travail de la force centrale. Calculer la puissance. P = F. v = -mw2 r. v r = a cos ( wt) i + b sin (wt) j ; v = -aw sin ( wt) i + bw cos (wt) j ; r. v =- a2w cos ( wt)sin ( wt) + b2w cos ( wt)sin ( wt) r. v =(b2 - a2)w cos ( wt)sin ( wt). P = mw3(a2 - b2)cos ( wt)sin ( wt). Montrer que le travail effectué en faisant faire au point M un tour complet est nul. Conclure. W = ½mw2  (r2départ- r2fin). Les points de départ et d'arrivée sont les mêmes, le travail est donc nul  en faisant un tour complet. Le travail d'une force conservative le long d'une courbe fermée est nul. Calculer l'énergie potentielle du système. En déduire le travail fourni en déplaçant le point de A en B. Une force centrale conservative f(r) dérive d'une énergie potentielle Ep(r) telle que : f(r) = -dEp(r) / dr avec f= -mw2 r. Le travail fourni   en se déplaçant de A en B est égal  à l'opposé de la variation de l'énergie potentielle : W = Ep(A)-Ep(B) =  ½mw2  (rA2- rB2).   .

retour -menu