Flux thermique à travers une gaine cylindrique : loi de Fourier

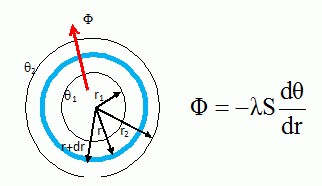q1  >q2 : le flux thermique F traverse la gaine isolante de l'intérieur vers l'extérieur. On note L la longueur du tube ; l : conductivité thermique de l'isolant ( W m-1 K-1). Par raison de symétrie, le transfert de chaleur par conduction est radial. S : aire latérale du cylindre de rayon r : S = 2 p r L. Par suite F = -l 2 p r Ldq/dr Le flux thermique est constant  dans tout le cylindre de rayon r compris entre r1 et r2 : 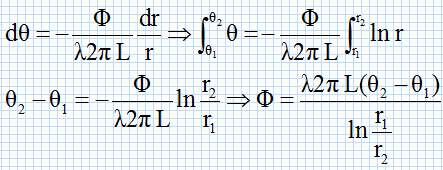AN : L = 1 m ; l = 1 Wm-1 K-1 ; q1 = 305 °C ; q2 = 293 °C ; r1 = 20 cm ; r2 = 25 cm. F =1*2*3,14*1*(293-305) / ln(0,20/0,25)=3,77 102 ~3,8 102 W. . Définir et calculer la résistance thermique de la longueur Lde gaine. Quelle analogie peut-on faire ? La résistance thermique de conduction R exprime l'opposition au passage d’un flux de conduction thermique. R = (Tc-Tf)/ F. Tc : température (en kelvin) surface chaude ; Tf : température (K) de la source froide ;  F : flux thermique ( W). R = ln (r2/r1) / (2plL). R = ln(0,25/0,20) / (1*2*3,14) =3,28 10-2 ~3,3 10-2 K W-1.   On améliore l’isolation du matériau en rajoutant une gaine supplémentaire d’épaisseur e’, de conductivité thermique l’=0,05W m-1 K-1.  Quelle doit être la valeur de e’ pour que les pertes thermiques soient divisées par 10 ? Les résistances thermique s'ajoutent : Rtotale = (Tc-Tf)/ F avec (Tc-Tf) inchangé et F divisé par 10. Donc Rtotale =10 R ; la résistance thermique du nouveau matériau est égale à 9 R = 9* 3,28 10-2 =0,295 K W-1. ln(r2/r1) / (2pl' L)= 0,295 ; ln(r2/r1) =0,295 (2pl'L)=0,295*6,28*0,05 =9,27 10-2.  r2/r1 =1,097 ~1,1 ;  r2/r1 -1 = 0,1 ; (r2 - r1 ) / r1 = 0,1 ; r2 - r1 = 0,1 r1 = 0,1*0,25 = 0,025 m = 2,5 cm. Flux thermique : On considère, un cylindre homogène en cuivre, de longueur b et de rayon a, parcouru par un courant électrique uniforme et constant d'intensité I. Caractéristiques du cylindre dans les conditions de l'étude : • résistivité électrique r=2,0.10-8 W m ; • conductibilité thermique : l = 400 W K-1m-1. • a=1,0 mm.   On suppose que l'énergie thermique produite dans le conducteur est dissipée radialement par conduction et on néglige les effets de bord. On rappelle que la résistance R d’un conducteur cylindrique homogène résistivité électrique r, de longueur b et de section S, est donnée par la relation : R=rb/S Exprimer la puissance p dissipée par unité de volume en fonction des paramètres r, a et I. Exprimer le flux thermique de conduction F (r) qui traverse une surface cylindrique de longueur b et de rayon r (r<a) En faisant un bilan thermique sur l'élément de volume compris entre les surfaces cylindriques de rayons r et r+dr, montrer que la température T satisfait l'équation différentielle suivante : d(rdT/dr)/dr= -p/l r. Intégrer cette équation. En déduire l'expression de l'écart de température DT entre l'axe et la surface. Calculer DT pour I=20 A. Commenter. corrigé puissance P dissipée : P= RI² avec R=rb/S et S= pa² ; p= rbI²/(pa² ) volume du cylindre V= pa²b puissance p dissipée par unité de volume p= P/V = rI²/(pa² )2 en Wm-3. flux thermique de conduction qui entre par une surface cylindrique de longueur b et de rayon r : -l* surface latérale de rayon r * dT/dr = -l 2pr b(dT/dr )r. flux thermique de conduction qui sort par une surface cylindrique de longueur b et de rayon r+dr : -l* surface latérale de rayon r +dr * dT/dr = -l 2p(r+dr)b(dT/dr )r+dr. élément de volume compris entre les surfaces cylindriques de rayons r et r+dr : dv= 2prbdr puissance interne dans cet élément de volume : pdv = 2pbp rdr bilan énergétique en régime permanent : 2pbp rdr -l 2pr b(dT/dr )r. + l 2p(r+dr)b(dT/dr )r+dr=0 p rdr -l r [dT/dr ]r + l (r+dr)[dT/dr ]r+dr=0 p rdr +l d (r dT/dr )=0 ou -pr/ l= d(rdT/dr)/dr d(rdT/dr)/dr= -p/l r s'écrit : dT/dr+ r d²T/dr²+p/l r =0 solution du type T= ar²+br+c ; dT/dr= 2ar+b ; d²T/dr²= 2a. 2ar+b+ 2ar + p/l r =0 soit b = 0 et a = - p/(4l) ; T= - p/(4l)r² + c; si r =0, T=c=T0 ; si r = a, T= -p/(4l) a² +T0 ; DT= p/(4l) a². or p= rI²/(pa² )2 d'où DT= rI²/(p2a² 4l). application numérique : DT=2 10-8*400/(3,14²*10-6*4*400)=0,005 °C. la section du fil est proche de 3 mm², celui-ci est tout à fait capable de supporter sans dommage un courant d'intensité 20 A. conducteur et gaine isolante : Soit un conducteurde rayon r0, parcouru par un courant d'intensité I, entouré d'une gaine isolante d'épaisseur "a". La temprétature extérieure à la gaine constante vaut T0. Le conducteur a une conductivité électrique g et d'une conductivité thermique l1. La conductivité thermique de la gaine est l2. Le régime est stationnaire et on néglige les effets de bords ; on suppose le contact thermique parfait entre la gaine et le conducteur. Déterminer la températureT(r) dans le conducteur et dans la gaine.   corrigé Le conducteur seul : ( indice 1 pour le conducteur; indice 2 pour la gaine) puissance "p" dissipée (effet joule) par unité de volume V : p= RI² / V avec R=(1/g)L/S et S= p r0² section (m²) ; volume du cylindre V= p r0²L puissance "p" dissipée par unité de volume p= P/V = (1/g) I²/(pr0² )2 en Wm-3. flux thermique de conduction qui entre par une surface cylindrique de longueur L et de rayon r :   -l1* surface latérale de rayon r * dT1/dr = -l 2pr L(dT1/dr )r. flux thermique de conduction qui sort par une surface cylindrique de longueur L et de rayon r+dr : -l1* surface latérale de rayon r +dr * dT1/dr = -l 2p(r+dr)L(dT1/dr )r+dr. élément de volume compris entre les surfaces cylindriques de rayons r et r+dr : dv= 2prLdr puissance interne dans cet élément de volume : pdv = 2pLp rdr bilan énergétique en régime permanent : 2pLp rdr -l1 2pr L(dT1/dr )r. + l1 2p(r+dr)L(dT1/dr )r+dr=0 p rdr -l1 r [dT1/dr ]r + l1 (r+dr)[dT1/dr ]r+dr=0 p rdr +l1 d (r dT1/dr )=0 ou -pr/ l1= d(rdT1/dr)/dr d(rdT1/dr)/dr= -p/l1 r s'écrit : dT1/dr+ r d²T1/dr²+p/l r =0 solution du type T1= ar²+br+c ; dT1/dr= 2ar+b ; d²T1/dr²= 2a. 2ar + b + 2ar + p/l r =0 par identification il vient : soit b = 0 et a = - p/(4l1) ; T1= - p/(4l1)r² + c La constante "c" sera déterminée à partir de l'expression de T2(r), température dans la gaine gaine isolante : même méthode bilan énergétique en régime permanent : -l2 2pr L(dT2/dr )r. + l2 2p(r+dr)L(dT2/dr )r+dr=0 -l2 r (dT2/dr )r. + l2 (r+dr)(dT2/dr )r+dr=0 l1 d (r dT2/dr )=0 ; d (r dT2/dr )=0 ; r dT2/dr = constante = C dT2= C dr/ r ; T2= C ln r + C1, ( C1 est une constante d'intégration ) C est déterminée en écrivant la continuité du flux thermique en r= r0 : -l1 2pr L(dT1/dr )r = -l2 2pr L(dT2/dr )r -l1 (dT1/dr )r0 = -l2 (dT2/dr )r0 (dT1/dr )r0 = - p/(4l1)2r0 dr; (dT2/dr )r0 =C/r0dr ½pr0 = -l2C/r0 C= -½p r²0 / l2 C1 est déterminée en écrivant que T2= T0 en r = r0+a : T0= C ln (r0+a)+ C1 ; C1 = T0 -C ln (r0+a) T2= C ln r + T0 -C ln (r0+a) =T0 -C ln( r /(r0+a))= T0 - ½p r²0 / l2 ln( r /(r0+a)) On détermine c en écrivant la continuité de la température en r = r0 : T1(r0)= - p/(4l1)r0² + c ; T2(r0)= T0 - ½p r²0 / l2 ln( r0 /(r0+a)) - p/(4l1)r0² + c = T0 - ½p r²0 / l2 ln( r0 /(r0+a)) c = T0 - ½p r²0 / l2 ln( r0 /(r0+a))+ p/(4l1)r0² T1= T0 - ½p r²0 / l2 ln( r0 /(r0+a))+ p/(4l1)( r0² - r² ) ..

retour -menu