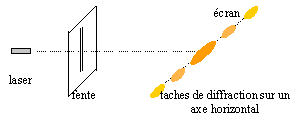Prisme : dispersion ; diffraction par une fente, puissance rayonnée par le soleil.

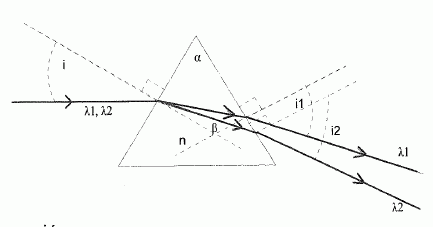
Etude d'un prisme Un sprisme possède un indice n qui dépend de la longueur d'onde l selon la loi : n = A +B/l2. A = 1,52 ; B = 1,700 104 nm2 ; a= 60° ; ce prisme est éclairé par un faisceau bichromatique : l1 = 750 nm et l2 = 400 nm. Déterminer n(l1) et n(l2) avec la précision appropriée. n(l1) = 1,520 + 1,700 104 / 7502 =1,55022~ 1,550. n(l1) = 1,520 + 1,700 104 / 7502 =1,62625~ 1,626. Calculer i1 et i2 ( l'angle d'incidence  i vaut i = 40 ° ; l'indice de l'air est égal  à 1). Réfraction sur le dioptre air-verre. Loi de Descartes : sin 40 = 1,55022 sin r1 ; sin r1 =0,4146 ; r1 =24,5°. Réfraction sur le second dioptre verre-air : angle d'incidence i'1 : a + b = 180 ; b = 120° ; b +r1+i'1 = 180 i'1 =60-24,5 = 35,5 °. 1,55022 sin i'1 = sin i1 ; sin i1 = 0,900 ; i1 = 64,186 ° ~ 64°. Calcul identique avec l'autre radiation ( n = 1,62625). sin 40 = 1,62625 sin r2 ; sin r2 =0,3952 ; r2 =23,28°. Réfraction sur le second dioptre verre-air : angle d'incidence i'2 : a + b = 180 ; b = 120° ; b +r2+i'2 = 180 i'2 =60-23,28 = 36,72 °. 1,62625 sin i'2 = sin i2 ; sin i2 = 0,9722 ; i2 = 76,48 ° ~ 76° Citer le phénomène responsable de l'élargissement du faisceau. Précier les couleurs des deux longueurs d'onde. Le prisme est un milieu dispersif pour la lumière. 400 nm : violet ; 750 nm : rouge. Si l'angle d'incidence i est trop petit, le rayon entrant dans le prisme ne peut pas émerger après double réfraction. Justifier et calculer l'angle limite d'incidence. Sur le second dioptre verre-air, l'angle limite d'incidence est tel que  sin i'1 lim = nair / nprisme = 1/1,55022 =0,645 ;  i'1 lim =40,17 °. Si  l'angle d'incidence est supérieur à  i'1 lim  , il y a réflexion totale sur le second dioptre. angle de réfraction sur le premier dioptre : r1 = 60 - i'1 lim =60-40,17 = 19,83 sin i = 1,55022 sin r1 =1,55022 sin 19,83 =0,526 ; i = 31,7 ~ 32°. Calcul identique avec l'autre longueur d'onde ( indice : n = 1,62625). sin i'2 lim = nair / nprisme = 1/1,62625 =0,615 ;  i'2 lim =37,95 °. angle de réfraction sur le premier dioptre : r2 = 60 - i'2 lim =60-37,95 = 22,05 sin i = 1,62625 sin r2 =1,62625 sin 22,05 =0,611 ; i = 37,6 ~ 38°.   Lampe  à vapeur de sodium Le sodium sous forme de vapeur chauffée émet 94 radiations dont deux, très intenses, sont de couleur jaune et dont les longueurs d'onde dans l'air à 101 325 Pa et 20 °C ont pour valeur 588,995 0 nm et 589,592 4 nm. On donne la célérité de la lumière dans le vide : c = 299 792 458 m.s-1.  Indiquer, en justifiant, le type de lumière (monochromatique ou polychromatique) émise par une lampe à vapeur de sodium. Monochromatique : une seule fréquence, une seule couleur ; polychromatique : plusieurs fréquences, plusieurs couleurs. "émet 94 radiations" : la lumière émise est polychromatique. L'indice de réfraction de l'air à 101 325 Pa et 20 °C vaut n = 1,000 273. Calculer la longueur d'onde dans le vide de chacune des deux radiations de l'énoncé. l0 = c / n avec n fréquence constante quel que soit le milieu. lair = vair / n et n = c /vair . par suite l0 =n lair. 588,995 0 *1,000 273=589, 155 8 nm. 589,592 4 *1,000 273=589,753 3 nm. Calculer la fréquence de chacune de ces deux radiations dans le vide, puis dans l'air. La fréquence ne dépend pas du milieu de propagation : elle est identique dans l'air et dans le vide. n = c/l ; 299 792 458 / 588,995 0 10-9 =5,089 898 1014 Hz. 299 792 458 / 589,592 4 10-9 =5,084 741 1014 Hz. Un faisceau de la lumière émise par la lampe à vapeur de sodium est dirigée sous une incidence d'environ 60° sur une face d'un prisme ayant pour section droite un triangle équilatéral.  Indiquer ce que l'on observe lors de l'émergence du faisceau lumineux. Préciser le nom donné à ce phénomène. Le prisme est un milieu dispersif pour la lumière. On observe deux rayons lumineux  de couleur jaune, déviés différemment après réfraction. Seule la radiation de 588,995 0 nm est dirigée vers une fente F de largeur a = 50 μm. Sur un écran placé à une distance D = 1,2 m à l'arrière de la fente, une figure apparaît. Indiquer le nom associé à ce phénomène. Diffraction par une fente dont les dimensions sont proches de la longueur d'onde de la lumière.  Représenter schématiquement l'expérience et l'aspect de la figure observée. 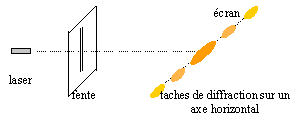Calculer la valeur ½L de la distance séparant le milieu de la frange centrale de la première extinction. 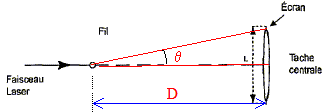tan q = ½L/D voisin de q radian pour les angles petits. d'autre part q = l/a. avec : l longueur d'onde (m) et a : largeur de la fente (m) 2l/a=L/D soit ½L=lD/ a =588,995 10-9 *1,2/ 50 10-6 =0,0141 m ~1,4 cm. Puissance rayonnée par le soleil : Le rayonnement solaire met en moyenne 500 s à nous parvenir. Avant d'entrer dans l'atmosphère terrestre, la puissance moyenne de ce rayonnement par unité de surface perpendiculaire  à la direction Soleil-Terre est FS=1370 W m-2. Au cours de l'année, la valeur de FS varie de plus ou moins 3%. Quelle est la cause de cette légère variation ? Variation de la distance Soleil-Terre au cours de l'année ; inclinaison de la Terre ;présence ou absence de taches solaires. Déterminer la distance Soleil-Terre. distance (m) = célérité de la lumière dans le vide (m /s) * durée (s) d = 3,0 108 *500 = 1,5 1011 m . En utilisant la 3è loi de kepler, déterminer la masse du Soleil (G = 6,67 10-11 S.I). L'orbite de la Terre est assimilé  à un cercle de rayon R =1,5 1011 m ; la Terre décrit son orbite en 365 jours : T = 365*24*3600 = 3,15 107 s. 3è loi de Kepler : T2 / R3 = 4 p2/(GM) avec M : masse du soleil. M= 4 p2R3/(GT2) = 4,3,142 *(1,5 1011)3 /(6,67 10-11* (3,15 107)2) =2,0 1030 kg. Montrer par le calcul que la puissance rayonnée par le Soleil vaut PS = 3,9 1026 W. Le Soleil rayonne dans toutes les directions. Aire d'une sphère de rayon R = 1,5 1011 m : S = 4 p R2 = 4*3,14 *(1,5 1011)2 = 2,83 1023 m2. PS = FS * S = 1370 *2,83 1023 =3,9 1026 W. Préciser le phénomène  à l'origine de l'énergie solaire. Réaction de fusion nucléaire. Calculer la perte de masse subie par notre étoile à chaque seconde. E = Dm c2 avec E = 3,9 1026 J perdus en  une seconde. Dm  = E / c2 =3,9 1026 /9 1016 =4,3 109 kg s-1. L'âge du Soleil est évalué  à 4,5 milliards d'années. Quelle fraction de sa masse at-il perdue depuis qu'il rayonne ( on suppose que la puissance produite est restée constante). 4,5 109 ans = 4,5 109*365*24*3600 s = 1,42 1017 s. Masse perdue : 4,3 109 *1,42 1017 =6,1 1026 kg. Puis diviser par la masse du Soleil : 6,1 1026 / 2 1030 =3,0 10-4 ( 0,03 %) Déterminer la valeur de l'énergie solaire reçue actuellement sur la Terre sachant que le rayon terrestre vaut 6400 km. Aire d'une sphère de rayon R = 6,4 106 m : S = 4 p R2 = 4*3,14 *(6,4 106)2 = 5,15 1014 m2. PS = FS * S = 1370 *5,15 1014 =7,1 1017 W. Energie ( J) = puissance (W) * durée (s) 365 jours = 365*24*3600 s =3,15 107 s Energie reçue annuellement par la Terre : 3,15 107 *7,1 1017 =2,2 1025 J. Chaque humain consomme en moyenne 1000 W. L'énergie solaire pourra t-elle, une fois maitrisée, subvenir aux besoins de l'humanité ? 7,1 1017 / 1000 =7,1 1014 humains, valeur supérieure à 7 milliards d'habitants actuellement. L'énergie solaire pourra subvenir aux besoins de l'humanité.

retour -menu