Disque en rotation, étude d'un mouvement rectiligne, lois de Newton, énergie mécanique

Disque en rotation. Un disque plan, entraîné par un moteur, est animé d'un mouvement de rotation uniforme autour d'un point O : il tourne  à la vitesse de rotation N = 300 tours / minute.. Calculer la période et la fréquence de rotation. Le disque effectue 300 / 60 = 5 tours / s ; la fréquence est égale à f = 5,0 Hz. La période, durée pour effectuer un tour, est T =1 / 5 = 0,20 s. Calculer la vitesse angulaire w0 ( rad/s). w0 = 2 p f = 2*3,14*5,0 = 31,4 ~ 31 rad/s. De quel angle ( degré ) tourne le disque en  10 ms ? Dt =10 ms = 10 10-3 s. Angle de rotation  : w0 Dt = 31,4 *10 10-3 =0,314 radian. soit 0,314 / 3,14*180 =  18°. Un point A est situé  à la distance rA=8,0 cm de O. Quelle est la norme du vecteur vitesse de ce point ? vA = w0 rA=31,4 * 8,0 10-2 =2,5 m/s. Un point B est situé  à la distance rB = 4,0 cm de O. Les points A, B et O sont alignés. B est entre O et A. Comparer, à une même date, les vecteurs vitesse des point A et B. vB = w0 rB= w0 rA/2 = ½vA. 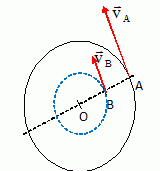Les vecteurs vitesse sont portés par la tangente au cercle au point considéré ; ces vecteurs ont le sens du mouvement.   Le moteur est débrayé : il nentraîne plus le disque. Le disque ralentit. Sa vitesse angulaire w  varie en fonction du temps, suivant la relation w = w0-at ( a est un coefficient constant ). L'origine des dates est  choisie  à l'instant  de débrayage du moteur. Sachant que sa vitesse angulaire a diminué de moitié  à la date t1 = 30 s, calculer : Les valeurs des vitesses des points A et B à la date t1. vA = ½w0 rA=0,5*31,4 * 8,0 10-2 =1,26 m/s ~1,3 m/s. vB =½vA = 0,5*1,26 =0,63 m/s. La valeur du coeficient a en précisant son unité. a x t est homogène  à :  rad s-1 ; le temps est en seconde : a est en rad s-2. a = ( w0-w) / t1 = ½w0 / t1 =0,5*31,4/30 =0,5233 ~0,52 rad s-2. La date d'arrêt du disque. w0-at = 0 ; t =  w0/a =31,4 / 0,523 = 60 s.     Etude d'un mouvement rectiligne. Un mobile est en translation sur un axe horizontal. Le schéma ci-dessous indique les positions du centre d'inertie G du mobile à différents instants séparés par un intervalle de temps constant Dt = 10 ms. Déterminer les vitesses du point G aux instants t2 et t4. v2 = (M1M2 + M2M3) / (2Dt) avec M1M2 et M2M3 mesurées  à la règle sur le dessin. M1M2 ~ 6 mm  = 6 10-3 m et  M2M3 ~ 11 mm  = 1,1 10-2 m ; Dt = 1,0 10-2 s. v2 = (6 10-3 + 1,1 10-2) / ( 2,0 10-2) =0,85 m s-1. v4 = (M3M4 + M5M4) / (2Dt) avec M3M4 et M5M4 mesurées  à la règle sur le dessin. M3M4 ~ 15 mm  = 1,2 10-2 m et  M5M4 ~ 19 mm  = 1,9 10-2 m ; Dt = 1,0 10-2 s. v4 = (1,2 10-2 + 1,5 10-2) / ( 2,0 10-2) =1,35 ~1,4 m s-1. 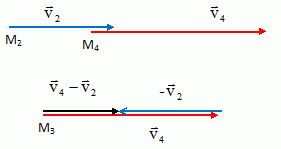Représenter ces deux vecteurs ( échelle 1 cm <--> 0,2 m/s) ainsi que le vecteur différence de ces deux vecteurs. 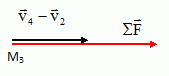En déduire la direction et le sens du vecteur somme des forces agissant sur le mobile au voisinage du point M3. 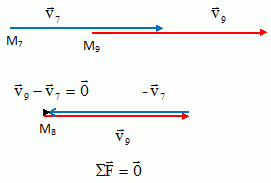Déterminer les vitesses du point G aux instants t7 et t9. Conclure quant  à la somme vectorielle des forces  agissant sur le solide au voisinage du point M8. v7 = (M6M7 + M7M8) / (2Dt) avec M6M7 et M7M8 mesurées  à la règle sur le dessin. M6M7 ~ 24 mm  = 2,4 10-2 m et  M7M8 ~ 24 mm  = 2,4 10-2 m ; Dt = 1,0 10-2 s. v7 = (2,4 10-2 + 2,4 10-2) / ( 2,0 10-2) =2,4 m s-1. v9 = (M8M9 + M9M10) / (2Dt) avec M8M9 et M9M10 mesurées  à la règle sur le dessin. M8M9 ~ 24 mm  = 2,4 10-2 m et  M9M10 ~ 24 mm  = 2,4 10-2 m ; Dt = 1,0 10-2 s. v9 = (2,4 10-2 + 2,4 10-2) / ( 2,0 10-2) =2,4 m s-1.   Un solide en acier de masse m = 30,0 g peut se déplacer sur un plan incliné d'un angle α = 35,0° avec l'horizontale. En D, le solide passe avec une vitesse VD acquise à l'aide d'un ressort. On peut considérer les frottements comme négligeables dans cette partie, lorsque le solide glisse sur le plan. Intensité du champ de pesanteur au niveau du sol : g = 9,80 m.s-2. 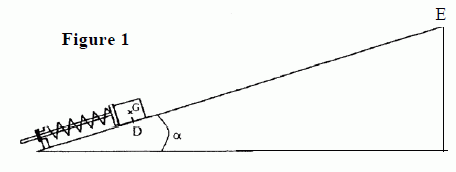La position du centre d'inertie G du solide est repérée sur un axe x'x de même direction que la ligne de plus grande pente du plan incliné et orienté vers le haut. 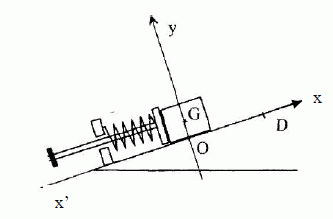On tire sur la tige et on comprime ainsi le ressort jusqu'à ce que le centre d'inertie du solide se trouve au point O, puis on lâche la tige. Lorsque le centre d'inertie du solide arrive en D, le ressort est bloqué et le solide est libéré. La figure suivante représente à l’échelle 1 les positions occupées par le centre d'inertie G du solide pendant la phase de propulsion à des intervalles de temps réguliers τ = 20,0 ms (points M0 à M5). A t = 0 le centre d'inertie du solide est au point O ou MO.   Déterminer à 10-3 près les vitesses V2 et V4 du solide aux points M2 et M4 en effectuant des mesures sur la figure. V2 = (M1M2 + M2M3) / (2t) =(3,2 + 4,3) 10-2 / (2*0,040) =0,9375 ~0,938 m s-1. V4 = (M3M4 + M4M5) / (2t) =(4,8 + 5,1) 10-2 / (2*0,040) =1,2375 ~1,24 m s-1. Exprimer le vecteur accélération a du solide au passage du point M3 en fonction des vitesses V2 et V4 et de l’intervalle de temps τ. En déduire la valeur de cette accélération a. 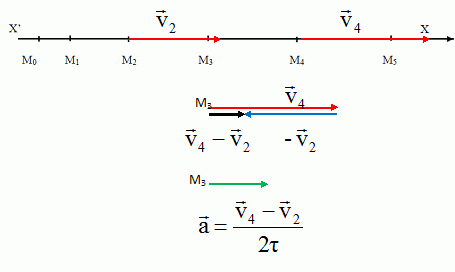a = (1,2375-0,9375) / (2*0,040) =3,75 m s-2.   En D la vitesse du solide est VD = 2,00 m.s-1. Il glisse ensuite jusqu'au point E où il s'arrête. Dans cette partie du mouvement, on prendra la position du centre d'inertie du solide en D comme origine des altitudes (ZD = 0) et comme niveau de référence de l'énergie potentielle de pesanteur : EPP(D)=0. Représenter sur un schéma les forces qui s'appliquent au solide sur le trajet DE. 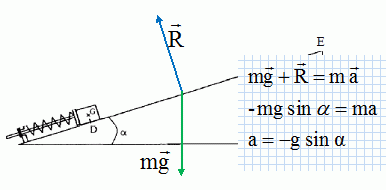Donner l'expression au point D de l'énergie mécanique Em(D) du solide en translation dans le champ de pesanteur. L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. Em(D) = ½mv2D+mgZD  avec ZD =0 ; Em(D) = ½mv2D. Donner l'expression de l'énergie mécanique Em(E) du solide au point E, en fonction de m, g, α et de la distance DE. Em(E) = ½mv2E+mgZE  avec VE =0 ; Em(E) = mgZE = mg DE sin a. En admettant que l'énergie mécanique du solide en translation dans le champ de pesanteur se conserve, calculer la valeur de la distance DE. Em(D) =Em(E) ; ½mv2D =mg DE sin a ; DE =v2D /(2gsin a )=4/(2*9,8*sin35)=0,3558 ~0,356 m.

retour -menu