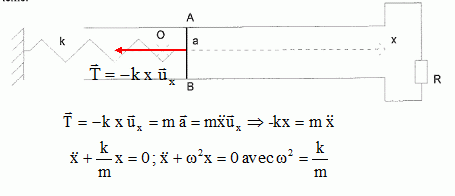Question 1.
Une
tige AB horizontale, de masse m, de longueur a, peut glisser sans
frottement sur deux rails horizontaux. la tige AB est liée à un ressort
de constante de raideur k.
L'origine O de l'axe x correspond à un allongement nul du ressort.
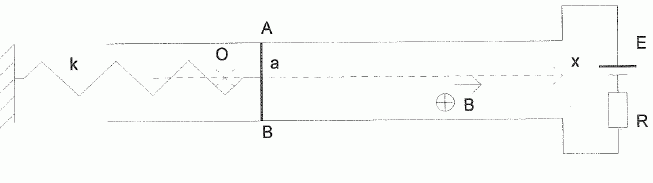
La tige AB permet de fermer le circuit électrique constitué
d'une résistance r et d'un générateur de fem E ( les résistances de la
tige et des rails sont négligeables devant R).
La tige au repos est placée dans un champ magnétique vertical B.
Etude statique.
Exprimer I, courant traversant la tige, orienté de A vers B, en
fonction de E et R.
I = E/R.
Définir
toutes les forces s'exerçant sur la tige AB.
La tige AB, placée dans un champ magnétique et traversée par un courant
est soumise à une force de Laplace F.
Poids de la tige, vertical, vers le bas, valeur mg ; action des rails,
verticale, vers le haut, opposée au poids.
Tension du ressort, horizontale, vers la gauche, valeur T = k (l-l0)
= kx.
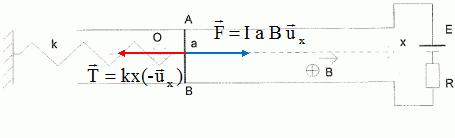
|
Déterminer
l'allongement x du ressort en fonction de E, R, B, a et k.
A l'équilibre la tension du ressort et la force de Laplace sont
opposées : elles ont même valeur :
kx = I a B = E a B / R ; x = E a B / (R k).
|
Etude dynamique
sans champ magnétique :
Le générateur est enlevé et le circuit est fermé sur lui même.
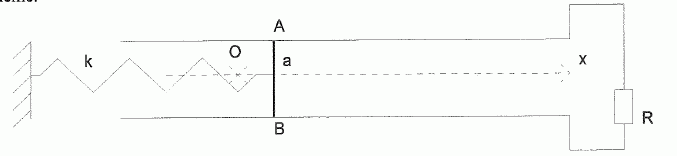
On lâche la tige AB sans vitesse initiale, depuis une position initiale
x(t=0) = x1.
Déterminer
l'équation du mouvement ultérieur de la tige.
La tige AB est soumise à son poids, à l'action des rails (
opposée au poids) et à une force de rappel exercée par le ressort.
Ecrire
la seconde loi de Newton sur l'axe Ox.
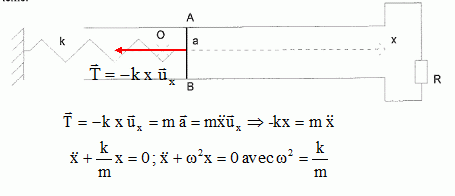
Montrer
que la solution peut s'écrire : x(t) = xm cos ( 2pt/T +f).
x' = -xm
2p/T sin ( 2pt/T +f) ; x" =-xm (2p/T )2 cos ( 2pt/T +f) avec : w2 = (2p / T )2= k / m.
Repport dans l'équation différentielle :
-xm (2p/T )2 cos ( 2pt/T +f) + k/m xm cos ( 2pt/T +f) = 0
( (2p/T )2 -k/m) xmcos ( 2pt/T +f) = 0 est bien vérifiée quel que
soit le temps.
x(t)
= xm cos ( 2pt/T +f) est la solution générale de
l'équation différentielle.
Déterminer
T, xm et f.
T = 2p /w =2p (m / k )½.
A l'instant initial : x(0) = x1 = xm cos f ; f
= 0
et xm = x1( xm
est l'amplitude, valeur positive)
ou bien la vitesse initiale est nulle : x'(0) = 0 = -x1 2p/T sin f.
Etude dynamique
avec champ magnétique :
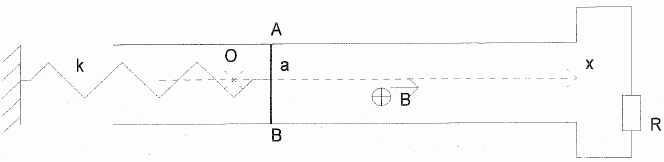
En présence du champ
magnétique et avec les mêmes conditions de lancement que précédemment,
il existe un courant i variable dans le temps, lors du mouvement de la
tige.
Déterminer
l'équation mécanique du mouvement de la tige en appliquant la seconde
loi de Newton à la tige AB. On fera apparaître dans cette
équation le courant i ( équation 1).
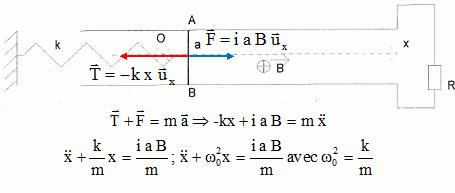
La tige AB, placée
dans un champ magnétique et traversée par un courant est soumise à une
force de Laplace F.
Par ces effets électromagnétiques cette force s'oppose à la cause qui
lui donne naissance, le déplacement de la tige.
Poids de la tige, vertical, vers le bas, valeur mg ; action des rails,
verticale, vers le haut, opposée au poids.
Force de rappel exercée par le ressort ; écrire
la seconde loi de Newton sur l'axe Ox.
Etude dynamique
avec champ magnétique :

En présence du champ
magnétique et avec les mêmes conditions de lancement que précédemment,
il existe un courant i variable dans le temps, lors du mouvement de la
tige.
Déterminer
l'équation mécanique du mouvement de la tige en appliquant la seconde
loi de Newton à la tige AB. On fera apparaître dans cette
équation le courant i ( équation 1).
La tige AB, placée
dans un champ magnétique et traversée par un courant est soumise à une
force de Laplace F.
Par ces effets électromagnétiques cette force s'oppose à la cause qui
lui donne naissance, le déplacement de la tige.
Poids de la tige, vertical, vers le bas, valeur mg ; action des rails,
verticale, vers le haut, opposée au poids.
Force de rappel exercée par le ressort ; écrire
la seconde loi de Newton sur l'axe Ox.
Exprimer l'énergie potentielle Ep,
l'énergie cinétique Ec puis l'énergie mécanique Em
de la tige.
Energie potentielle
élastique : Ep = ½kx2 ;
Les rails sont horizontaux ; cette position est choisie comme origine
de l'énergie potentielle de pesanteur.
Ec = ½mv2 ; Em = Ep+Ec =½kx2 +½mv2.
Exprimer la puissance
dissipée par effet Joule dans le circuit.
Pj = R i2.
sachant que la puissance
mécanique perdue -dEm/dt est dissipée par effet Joule, écrire la relation reliant x,
dx/dt = v et i .(équation
2)
dEm/dt = kx x' +
m v v' = kx v + m v v' ; avec x' = v = dx/dt et v' = a = x".
- (kx + mx") v = R i2. (2)
Exprimer simplement i en fonction de v,
a, B et R.
(1) donne : kx + mx" = i a B
repport dans (2) : i a B v = -R i2 ; a B v = R i ; i = -a B v / R.
Réécrire
l'équation mécanique de la tige relaint x, x' et x".
x" + k/m x = -(a B)2 /(m R) x'.
x" + (a B)2 /(m R) x' + k/m x = 0.
Préciser
la nature du mouvement si le champ magnétique est faible et si le champ
magnétique est intense.
Champ magnétique faible : le terme (a B)2 /(m R) est petit et
l'amortissement est faible : mouvement pseudo-périodique.
Champ magnétique fort : le terme (a B)2 /(m R) est grand et
l'amortissement est important : mouvement apériodique.
|
|
Un
conducteur AB peut se déplacer perpendiculairement à deux rails
conducteurs parallèles en présence d'un champ magnétique B uniforme
d'intensité 1 T tel qu'indiqué sur la figure ci-dessous. La longueur du
conducteur AB est de 1 m et sa résistance est de 1 W.
Les deux rails de résistance négligeable sont alimentés par un
générateur continu E = 10 V et de résistance interne négligeable.
En régime permanent la
vitesse du conducteur AB est de 7 m.s-1.
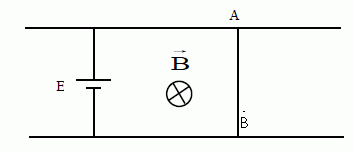
Déterminer le
courant circulant dans AB.
La
vitesse du conducteur étant constante, le principe d'inertie indique
que la somme vectorielle des forces appliquées à AB est nulle.
Le poids et l'action du support se neutralisent.
Le conducteur AB traversé par un courant
I et soumis à un champ magnétique est soumis à une force de
Laplace :
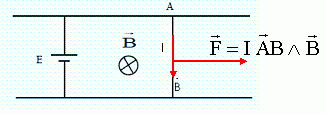
Un conducteur mobile
dans un champ magnétique est le siège d'une f.em
d'induction,
notée e= B x AB x v = 7 V, qui par ces effets électromagnétiques
s'oppose au déplacement du conducteur. Il en résulte un courant induit
et une force de Laplace induite telle que :
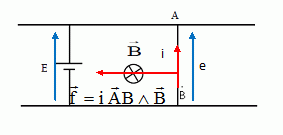
La tension aux bornes de AB vaut : uAB= E-e = 10-7 = 3 V ; 7 = R i d'où
i = 3 A.
Déduire
la puissance débitée par la source E.
P = E I = 10*3 = 30 W.
Déterminer
la puissance des pertes Joule dissipées dans le conducteur AB.
PJ
= R I2 = 1*32 = 9,0 W.
Déterminer
la puissance mécanique fournie par le conducteur AB.
F = I x AB x B = 3 *1 *1
= 3 N.
Puissance de cette force : F x v = 3 * 7 = 21 W.
Déterminer la
vitesse du conducteur AB pour que la puissance mécanique soit nulle.
La force de Laplace et
la vitesse étant colinéaires et de même sens, la
puissance mécanique est nulle si la force est nulle, c'est à dire si
l'intensité résultante est nulle.
Soit uAB=
E-e =0 ; e = E = 10 V ; e= B x AB x v = 10 V
; v = 10 m/s.
|
|