Force de Laplace.

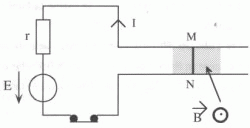
La barre MN peut se déplacer sur les rails parallèles horizontaux. La résistance électrique des rails et de la tige MN est négligeable. Les rails sont situés dans une région où règne un champ magnétique uniforme vertical. MN=d = 10,0 cm ; B = 0,020 T ; E = 12 V ; r=2,0 W. En l'absence de champ magnétique, exprimer puis calculer  l'intensité du courant I. E = r I ; I = E/r = 12/2,0 = 6,0 A. Donner la direction et le sens et la valeur de la force F agissant sur MN. La tige MN parcourue par un courant d'intensité I et placée dans un champ magnétique B est soumise à la force de Laplace. 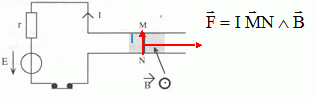F  = I MN B = 6,0 *0,10 *0,020 =0,012 N.   On supprime le générateur  et on le remplace par un ampèremètre très sensible. On déplace la tige vers la droite, l'ampèremètre décèle le passage d'un courant. Expliquer le phénomène. Quelle conversion d'énergie obtient-on ?  La tige MN est placée dans un champ magnétique etde plus est mise en mouvement : les deux conditions sont requises pour observer le phénomène d'induction magnétique ( passage d'un courant dans le circuit qui n'existe que pendant le déplacement de la tige) : c'est le principe de l'alternateur. De l'énergie mécanique ( déplacement de la tige) est convertie en énergie électrique ( passage d'un courant). Cadre rectangulaire. Un solénoïde de longueur L = 60 cm est constitué de N = 1200 spires circulaires de rayon 10 cm. Il est parcouru pr un courant d'intensité I' = 1,2 A. Un cadre carré de côté a = 4,0 cm parcouru par un courant I = 0,4 A est suspendu à l'intérieur du solénoïde. µ0 = 4 p 10-7 SI. Exprimer puis calculer la valeur du  champ magnétique à l'intérieur du solénoïde. B = µ0 n I' avec n = N/L = 1200 / 0,60 =2000 spires par mètre. B = 4*3,14 10-7*2000*1,2 =3,016 10-3 ~3,0 10-3 T. Représenter sur une vue de dessus les forces de Laplace agissant sur les côtés AD et BC. 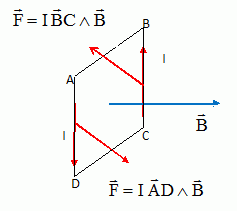Exprimer et calculer les valeurs des forces de Laplace agissant sur le cadre (ß =20°). F = I a B sin ß avec a = 0,040 m ; I =0,4 A et B = 3,0 10-3 T. Force de Lapalce agissant sur AB : F = 0,4 *0,04 * 3,0 10-3 sin 20 =1,6 10-5 N.  Le conducteur AB, traversé par le courant I, est mobile  ; placé dans un champ magnétique, il est soumis à la force de Laplace F. Un fil est attaché à la tige AB ; ce fil passe sur une poulie ; une masse m est fixée à l'autre extrémité du fil. La tige AB est immobile si F = T = mg avec F = B I AB. m = B I AB / g ; A.N :  AB = 6 cm ; I = 6 A ; B = 0,1 T ; g = 10 SI. m = 0,1*6*0,06 / 10 =0,036 kg = 3,6 g. On permutte les branchements du générateur. Les frottements seront négligés. Le champ magnétique existe seulement sur une distance d = 4 cm. La tige est initialement au repos. On note m = 8 g la masse de la tige ; I l'intensité du courant ; B la valeur du champ magnétique. Quelle est la nature du mouvement de la tige AB ? La tige est soumise  à son poids, à l'action des rails : ces forces verticales, de sens contraire, se neutralisent. La tige, traversée par un courant I, placée dans un champ magnétique, est soumise  à une force de Laplace notée F.   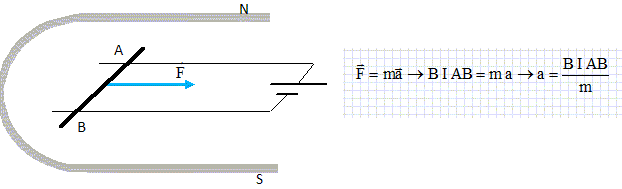L'accélération est constante : le mouvement est uniformément accéléré.  Vitesse v = a t = B I AB t / m.  Position sur un axe horizontal orienté vers la droite : x =½at2 = ½B I AB / m t2. Vitesse atteint après avoir parcouru la distance d= 4 cm = 0,04 m : t = v/ a ; d = ½a v2/a2 =  ½v2/a ; v2 = 2ad  ; v = (2ad)½. A.N : a = 0,1 *6 *0,06 / 0,008 =0,45 m s-2 ; v= (2*0,45*0,04)½=0,189 ~0,19 m/s. Au delà de cette distance d= 0,04 m, le conducteur n'est plus soumis qu'à son poids et à l'action des rails : ces actions se compensent. D'après le principe d'inertie, le mouvement est rectiligne uniforme à la vitesse v = 0,19 m/s. La tige parcourt 10 cm = 0,1 m en 0,1 / 0,189 =0,53 s. Un conducteur (AMNC) est constitué de trois partiees rectilignes de même section, de même masse m et de longueur L, formant trois cotés d’un carré pouvant tourner sans frottement autour d’un axe fixe horizontal passant par A et C. Ces deux extrémités sont reliées à un dipôle comprenant un générateur de tension continue (G), un rhéostat (Rh) un ampèremètre(A) et un interrupteur (K). Le cadre baigne dans un champ magnétique uniforme. (K) ouvert : le cadre occupe une position d’équilibre stable et verticale contenant l’axe fixe  horizontal. (K) fermé : le cadre occupe la position vue de profil.   Les côtés AM et CN, parallèles au champ magnétique ne sont pas soumis aux forces de Laplace. Le côté MN, perpendiculaire au champ magnétique est soumis à une force de laplace de valeur F = I MN B = I L B. On donne I = 1,0 A ; MN= L = 12 cm  = 0,12 m ; B = 0,20 T ; g = 10 N / kg ; m = 6,0 g = 6,0 10-3 kg. Lla tige MN est en équilibre sous l'action de son poids, de la force de laplace et de l'action des tiges AM et CN. tan a = 0,12 *0,20 / 0,060 =0,40 ; a = 21,8 ~22°.

retour -menu