Associations de générateur et de résistors : moteur, électrolyseur, calorimètre.

Un circuit électrique comprend disposés en série : un générateur (E = 24 V ; r = 3 ohms), un moteur ( E' = 8 V et r' = 3 ohms) et un fil conducteur de résistance R = 5 ohms. Calculer l'intensité I du courant. Additivité des tensions : Ugénérateur = Umoteur + UR ; E-rI =E'+r'I+RI d'où I = (E-E') / (r+r'+R) = (24-8) / (3+3+5) = 16 / 11 =1,454 ~1,5 A. Quelle est la tension aux bornes du générateur ? Ugénérateur =E-rI = 24-3*1,454 =19,6 V. On réalise un nouveau circuit en plaçant le moteur et la résistance aux bornes du générateur. Quelles sont les intensités du courant dans les différentes parties du circuit ? I : intensité principale ; I1 : intensité traversant le moteur ; I2 intensité traversant R. Loi des noeuds : I = I1 + I2 ; Ugénérateur = E-rI = 24-3I ; Umoteur = Ugénérateur =E'+r'I1=8+3I1 ; UR =Ugénérateur =RI2 = 5I2. 24-3I  = 5I2 ; I2 = 4,8-0,6I ; 24-3I  =8+3I1 ; I1 =5,33-I. Par suite : I = I1 + I2 = 4,8-0,6I +5,33-I d'où I = 3,9 A. I1 = 5,33-3,9 =1,43 ~1,4 A ; I2 = 4,8-0,6 *3,9 =2,46 ~2,5 A. Calculer l'énergie totale fournie par le générateur en 1 minute. W = E I t = 24*3,9*60 =5,6 103 J. Deux fils de cuivre F1 et F2 sont tels que F1 est deux fois plus long que F2 ; le diamètre du fil F2 est quatre fois plus petit que celui de F1. Trouver la relation entre les résistances R1 et R2 de ces fils. R1 = r L1 / S1 ; R2 = r L2 / S2 ; L1 = 2 L2 ; S1  = 16 S2 ; R1 = r 2L2 / (16S2 ) = r L2 / (8S2 ) ; R1 =R2 / 8.       Une spirale de maillechort de 3 m de longueur, parcourue par un courant I = 0,5 A est plongée dans un voltamètre ( électrolyseur ) à eau acidulée par l'acide sulfurique. Calculer la résistance R1 de la spirale sachant qu'un fil de même nature de 1 m de long, de section 5 fois plus grande a une résistance de 0,3 ohm. R1 = r L1 / S1 ; R2 = r L2 / S2 ; L1 = 3 L2 ; S2  = 5 S1 ; S1  = 0,2 S2 ; R1 = r 3L2 / (0,2S2 ) = 15 r L2 / S2 ; R1 =15 R2 ; R1 = 15*0,3 = 4,5 ohms. Calculer la quantité d'électricité qui circule dans le circuit en 1 heure. Q = I t = 0,5*3600 = 1800 C. Calculer le volume total des gaz ainsi que leur répartition . Quantité de matière d'électron : n(e-) = Q / F = 1800 / 96500 =1,865 10-2 mol. A la cathode : 2H+ + 2e- = H2(g) ; quantité de matière de dihydrogène : n(H2) = ½n(e-) =9,326 10-3 mol. Si le volume molaire vaut Vm = 22,4 L / mol, le volume de dihydrogène est : n(H2)Vm =9,326 10-3 *22,4 =0,21 L. A l'anode : H2O = ½O2(g) +2H+ + 2e- ; quantité de matière de dioxygène : n(O2) = 0,25n(e-) =4,66 10-3 mol. Le volume de dioxygène est : n(O2)Vm =4,66 10-3 *22,4 =0,105 L. Si ce courant traverse une cuve à électrolyse à nitrate d'argent, en combien de temps obtiendra-t-on 3,2 g d'argent à la cathode ? MAg = 108 g/mol ; l'argent est monovalent. Quantité de matière d'argent : nAg = m / MAg =3,2 / 108 =2,963 10-2 mol ;   Ag+ + e- = Ag(s) ; quantité de matière d'électron : n(e-) =nAg = 2,963 10-2 mol ; Quantité de matière d'électricité : Q=n(e-)* F =  2,963 10-2 * 96500 =2,86 103 C. Or Q = I t ; t = 2,86 103 / 0,5 = 5,72 103 s = 95,3 min = 1 h 35 min. Une spirale de maillechort de longuer L = 6 m et de section S1 = 0,3 mm2 est plongée dans un calorimètre en laiton pesant m =210 g et contenant m' =300 g d'eau et m" = 15 g de glace, le tout à 0°C. Chaleur massique du laiton c = 418 J K-1 kg-1 ; Chaleur massique de l'eau  c' = 4180 J K-1 kg-1 ; chaleur latente de fusion de la glace L = 3,34 105 J kg-1. Calculer la résistance de la spirale sachant qu'un autre fil de maillechort de longueur trois fois plus petite, de section 1 mm2 a une résistance R2 = 0,5 ohm. R1 = rL1/S1 ;  R2 = rL2/S2 ; L1= 3 L2 ; S1 = 0,3 S2 ; R1 = r 3 L2 / 0,3 S2 ; R1 = r 10 L2 / S2 = 10 R2 = 5 ohms. Calculer la durée de passage du courant I= 6 A pour amener la température du calorimètre à 8 °C. Energie nécessaire à la fonte de la glace : m" L = 0,015 *3,34 105 = 5,013 103 J. Energie nécessaire pour élever m'+m" g d'eau de 0 à 8 °C : (m'+m") c' Dq =0,315*4180*8 =1,053 104 J. Energie nécessaire pour élever m g de laiton de 0 à 8 °C : m c Dq =0,210*418*8 =7,02 102 J. Total W = 5,013 103 + 1,053 104 + 7,02 102 =1,625 104 J Or W = R1 I t ; t = W / (R1 I) =1,625 104 /(5*6) =5,42 102 s ~ 9 min.  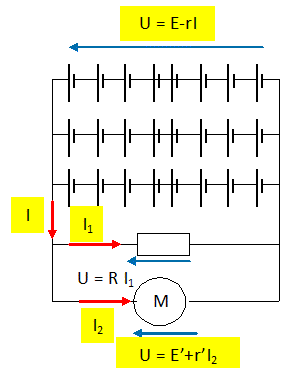On dispose de 24 éléments identiques disposés en 3 séries identiques de 8 éléments ( E = 12 V et r = 2 ohms ). Aux bornes de ce groupement on a placé deux branches en dérivation: la première contient une résistane R  3 ohms ; la seconde contient un moteur ( E' = 4 V et r' =2 ohms ) Faire le montage du circuit. Calculer la longueur du fil. R = 3 ohms ; diamètre d = 0,4 mm ; r = 62,8 10-8 Wm. R = r L/S ; l = RS / r avec S = pd2/4 =3,14 *(4 10-4)2/4 = 1,2566 10-7 m2. L = 3* 1,2566 10-7  / 62,8 10-8 = 0,6 m. Calculer la puissance du moteur. U = 12-2I = 3I1 ; I1 =4-2/3 I ; U = 12-2I = 4+2I2 ; I2 = 4-I. Loi des noeuds : I = I1 + I2 =4-2/3 I + 4-I d'où I = 3 A ; I1 = 2 A ; I2 =1 A. U = 6 V ; puissance  mécanique du moteur  E'I=4*1= 4 W. Calculer le rendement du générateur. U / E =6/12 =0,50. Calculer e' et r' de chaque élément. e' = E'/8 = 12/8 = 1,5 V. r = 8r'/3 ; r' =3r / 8 =6/8 = 0,75 ohm. Calculer l'énergie perdue par effet Joule dans chaque élément. Energie perdue en une seconde dans un élément : r'I'2 avec I' = I/3 = 1 A. 0,75*1 = 0,75 J s-1. On bloque le moteur, calculer le nouveau rendement du générateur. Moteur bloqué E'=0. U = 12-2I = 3I1 ; I1 =4-2/3 I ; U = 12-2I = 2I2 ; I2 = 6-I. Loi des noeuds : I = I1 + I2 =4-2/3 I + 6-I d'où I = 3,75 A ; I1 = 1,5 A ; I2 =2,25 A. U = 4,5 V ; rendement du générateur  U / E =4,5 / 12 = 0,375. Aux bornes d'un groupement de fem E = 36 V et de résistance r = 6 ohms on place une résistance R =12 ohms. Déterminer le groupement sachant que chaque élément a pour caractéristiques r' = 0,5 ohm et e' = 1,5 V. 36 / 1,5 = 24 éléments en série ; 24r' = 24*0,5 = 12 ohms. Le nombre de dérivations est noté n : 6 = 12 / n d'où n = 2. Il faut donc deux branches en dérivation comptant chacune 24 éléments. Calculer la longueur de la résistance R1 de 12 ohms sachant qu'un fil de même nature, de diamètre 3 fois plus petit, de résistanceR2=24 ohms, mesure 60 cm. R1 = rL1/S1 ;  R2 = rL2/S2 ; R1= ½ R2 ; S1 = 32 S2= 9S2 ; R1 = rL1 / (9S2) ; R2 = r *0,6 / S2 = 2 R1 =2 rL1 / (9S2) 0,6=2L1/9 ; L1 =0,3*9 =  2,7 m. Aux bornes de 48 éléments identiques aux premiers, on place une autre résistance R2 = 1,5 ohms. Déterminer le groupement pour que l'intensité soit maximale. La résistance du groupement doit être égale à r = R2 = 1,5 ohms. La résistance de chaque élément est r' = 0,5 ohm. Il faut donc 4 branches dérivées contenant chacune 12 éléments en série. r = 12 r' / 4 = 12*0,5/4 = 1,5 ohms. On remplace R2 par R3 et les éléments sont disposés en 4 séries de 12. Calculer R3 sachant que la puissance dépensée par  cette résistance est P = 30 W. E = 12*1,5 = 18 V ; r = 1,5 ohms ; I = E /(r+R3) ; P = R3I2 = R3[E /(r+R3)]2 = 30. 30(r+R3)2 = R3 E2 ; (1,5+R3)2 = R3 *182/30 =10,8 R3. 2,25 +3R3 +R32 =10,8 R3. ; 2,25 -7,8R3 +R32 =0 Discriminant D = 7,82-4*2,25 =51,84 ; D½ =7,2 ; R3 = (7,8 -7,2) / 2 =0,3 ohm ; autre valeur : R3 = (7,8+7,2) / 2 =7,5 ohms. Un circuit comprend un générateur, un interrupteur K, un ampèremètre de résistance négligeable et deux dérivations comprenant, l'une un voltamètre de résistance R1= 2,5 ohms et l'autre une résistance plongée dans un calorimètre contenant 500 g de pétrole de chaleur massique c = 2090 J K-1 kg-1. K étant ouvert, un voltmètre branché aux bornes du générateur G indique 14 V. K étant fermé, ce même voltmètre indique 10 V et l'ampèremètre 4 A. Calculer les caractéristiques de G. U = E-r I ; si I=0 ( K ouvert ), U = E = 14 V. K fermé : 10 = 14 -4 r d'où r = 1 ohm. Si l'élévation de température dans le calorimètre est alors de 4°C en 7 minutes, calculer : l'intensité du courant dans le calorimètre. Chaleur gagnée par le pétrole W = m c Dq =0,5 * 2090 *4 = 4180 J De plus W = U I t avec t = 7*60 = 420 s ; I = W /(Ut) = 4180/(10*420) ~ 1,0 A. la résistance du calorimètre. u = R I ; R = U / i = 10 / 1 = 10 ohms. Calculer la fcem  E' du voltamètre. U = E'+R1 I ; E' =  U-R1 I= 10-2,5*1 = 7,5 V. Avec 16 éléments identiques de fem e = 1,5 V et de résistance interne r' = 0,5 ohm, on fait un groupement qui débite dans une résistance en maillechort R = 2 ohms connectée seule aux bornes de G. Déterminer le groupement pour avoir une intensité maximale. La résistance du groupement doit être égale à r = R = 2 ohms. Donc 8 éléments en série  ( 8*0,5 = 4 ohms ) et deux branches dérivées comptant  chacune 8 élémrnts en série. Calculer l'intensité. E = 8*1,5 = 12 V ; i = E /(r + R) = 12/4 = 3 A. Calculer le dégagement de chaleur dans le fil de maillechort. Chaleur dégagée en une seconde : RI2 =2*32 = 18 J s-1.  Calculer la longueur du fil de maillechort de diamètre d = 0,8 mm sachant qu'un fil de maillechort de 1 m de long et de 1 mm de diamètre a une résistance de 0,35 ohm. R = rL1/S1 ;  R2 = rL2/S2 ; R2=0,35 /2 R = 0,175 R ; S1 = 0,82 S2= 0,64S2 ; R = rL1 / (0,64S2) ; R2 = r *1 / S2 = 0,175 R =0,175 rL1 / (0,64S2) 1=0,175L1/0,64 ; L1 =0,64 / 0,175 =  3,66 m. En dérivation avec R= 2 ohms, on place un voltamètre à eau acidulée et électrodes de platine de fcem E' = 1,5 V, de résistance r' = 5 ohms. Déterminer : le volume de dihydrogène dégagé en 1 min. 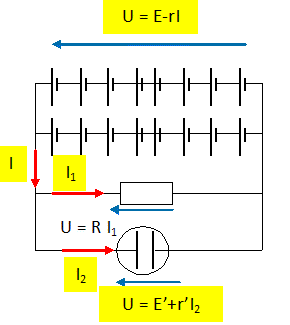U = 12-2I = 2I1 ; I1 =6- I ; U = 12-2I = 1,5 +5I2 ; I2 = 2,1-0,4I. Loi des noeuds : I = I1 + I2 =6- I + 2,1-0,4I d'où I = 3,375 A ; I1 = 2,625 A ; I2 =0,75 A. U =5,25 V ; quantité d'électricité Q = I2t = 0,75*60 = 45 C ; quantité de matière d'électrons n(e- ) =Q/F = 45/96500 =4,66 10-4 mol ; A la cathode : 2H+ + 2e- = H2(g) ; quantité de matière de dihydrogène : n(H2) = ½n(e-) =2,33 10-4 mol. Si le volume molaire vaut Vm = 22,4 L / mol, le volume de dihydrogène est : n(H2)Vm =2,33 10-4 *22,4 =5,2 10-3 L. la masse de zinc usée dans le générateur dans le même temps. ( MZn = 65 g/mol ; valence 2 ). quantité d'électricité Q = It =3,375*60 = 202,5 C ; quantité de matière d'électrons n(e- ) =Q/F = 202,5/96500 =2,1 10-3 mol; Zn(s) = Zn2+ + 2e- ; quantité de matière de zin n= ½n(e- ) = 1,05 10-3 mol. Masse de zinc : m = n MZn =1,05 10-3*65 =6,8 10-2 g.

retour -menu